Wstęp
W tej części kursu wkroczymy w trzeci wymiar! Dowiemy się jaka matematyka stoi za tym by uzyskać efekt 3D na płaskim monitorze, by potem wykorzystać tę wiedzę do stworzenia kolorowej piramidy. W tej części również nie będę umieszczał całego kodu tylko będę wskazywał i omawiał miejsca, które uległy zmianie od poprzedniej części. Solucję VC++ 2010 można pobrać tutaj. No to zaczynamy!
Teoria
By móc zrozumieć co tak naprawdę dzieje się w kodzie, musimy najpierw zapoznać się z matematyką - z przekształcaniem danych wierzchołków (głównie pozycji) do różnych przestrzeni odniesienia (układów współrzędnych). Może brzmi to dziwnie, ale w praktyce jest to dosyć proste.
Schemat transformacji
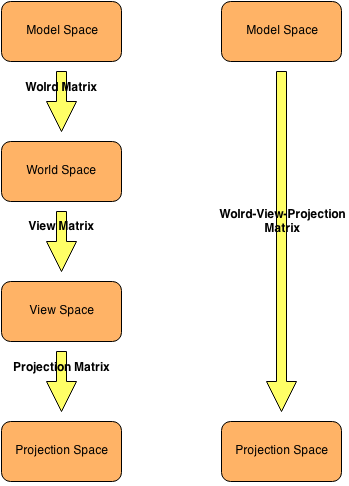
Każda pozycja i kierunek w świecie 3D należy do pewnego układu współrzędnych. Żeby przenieść daną pozycję/kierunek do innego układu musimy posłużyć się pewną macierzą transformacji (są to macierze 4x4). Najbardziej popularne macierze w programowaniu grafiki komputerowej to: macierz świata, widoku oraz projekcji. Poniższy diagram przedstawia standardowy zbiór transformacji jakie działają na geometrii trójwymiarowej.
Jak widzimy, by przejść z jednej przestrzeni do innej wystarczy pomnożyć wektor pozycji/kierunku geometrii przez odpowiednią macierz. Najważniejsze jest jednak, by dobrze zrozumieć te przestrzenie, aby można było się w nich swobodnie poruszać.
Przestrzeń lokalna (modelu)
Jest ona zbudowana z surowych danych pozycji wierzchołków dla danej geometrii (siatki), które nie zostały zmodyfikowane w żaden sposób. Są to dane, które najczęściej pochodzą z eksportu z jakiegoś programu do tworzenia modeli 3D (Maya, 3DS Max, Blender).
Przestrzeń świata
Współrzędne pozycji wierzchołków znajdują się teraz w przestrzeni świata (naszej sceny 3D). Kiedy pomnożymy wierzchołki znajdujące się w przestrzeni lokalnej przez macierz świata dostaniemy przekształcone wierzchołki (ich pozycje) w układzie świata (sceny). Te pozycje są szczególnie ważne przy ruszaniu obiektami na scenie jak i podczas obliczeń światła w programach cieniujących.
Przestrzeń widoku (kamery)
Współrzędne w tej przestrzeni są współrzędnymi w obszarze widzenia kamery. Pozycje wierzchołków (oraz inne dane wierzchołków) są ustawione względem wirtualnej kamery (oka) przez, którą obserwujemy tworzoną scenę. By przejść do tego układu odniesienia musimy pomnożyć pozycje wierzchołków znajdujące się w przestrzeni świata przez macierz widoku.
Przestrzeń jednorodna (projekcji)
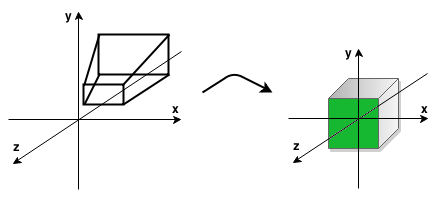
Jest to przestrzeń ekranu np. komputera. Kiedy pomnożymy macierz widoku przez macierz projekcji, wtedy obszar widzenia kamery (ścięta piramida) zostaje przekształcony w sześcian. Możemy podczas tej transformacji wziąć pod uwagę stosunek szerokości do wysokości ekranu (ang. aspect ratio) oraz kąt widzenia. Dzięki macierzy projekcji dostajemy wynik w postaci obrazu 3D na płaskim ekranie z wrażeniem głębi, perspektywy (obiekty bliżej kamery są większe, a obiekty znajdujące się dalej są mniejsze) oraz “ucina” geometrię (nie będzie ona rysowana), która znajduje się poza dwiema płaszczyznami obszaru widzenia kamery (bliska (ang. near) i daleka (ang. far) płaszczyzna). Obszar, który widzimy na ekranie jest oznaczony kolorem zielonym na obrazku poniżej.
Poniżej znajduje się finalny widok (obszar zaznaczony na zielono na obrazku powyżej):
Jedną z podstawowych czynności VerteX Shader’a jest to, by przekształcić pozycje wierzchołków do przestrzeni projekcji. Może to być zrobione w taki sposób, że do tego programu cieniującego przesyłamy macierze świata, widoku oraz projekcji i wykonujemy w nim trzy mnożenia przez pozycję wierzchołka. Można to oczywiście zoptymalizować, by odciążyć procesor graficzny. W tym celu wykonujemy mnożenia macierzy świata, widoku i projekcji w kodzie programu, by wszystkie mnożenia były wykonane przez CPU, a wynik był zapisywany w osobnej macierzy (skrótowo nazywana macierzą WVP), którą potem przesyłamy do Vertex Shader’a. Ograniczamy w ten sposób ilość danych jakie przesyłamy do GPU oraz ilość obliczeń, które GPU może spożytkować na coś innego.
Wyjaśnienie kodu
Po wstępie teoretycznym możemy mieć pytanie w stylu: “Wszystko fajnie z tymi macierzami, ale jak mam je stworzyć?”. Na pomoc przychodzi nam biblioteka GLM, która załatwia za nas wszystkie sprawy związane z częścią matematyczną i nie musimy nawet wiedzieć jak mają wyglądać te macierze (poza tym, że są to macierze 4x4). Jeżeli natomiast kogoś interesuje to w jaki sposób te macierze są konstruowane to odsyłam do informacji zawartych w Internecie.
No dobrze, przyjrzyjmy się teraz kodzie aplikacji. Chcemy przejść teraz w trzeci wymiar i chcielibyśmy narysować piramidę. W tym calu aktualizujemy tablicę wierzchołków:
GLuint programHandle = NULL;
glm::vec3 vertices [] = {glm::vec3 (-0.5 f,-0.5 f, 0.5 f), //basis
glm::vec3 (0.5 f,-0.5 f, 0.5 f),
glm::vec3 (0.5 f,-0.5 f,-0.5 f),
glm::vec3 (-0.5 f,-0.5 f, 0.5 f),
glm::vec3 (0.5 f,-0.5 f,-0.5 f),
glm::vec3 (-0.5 f,-0.5 f,-0.5 f),
glm::vec3 (-0.5 f,-0.5 f,-0.5 f), //left side
glm::vec3 (-0.5 f,-0.5 f, 0.5 f),
glm::vec3 (0 .0F, 0.5 f, 0 .0F),
glm::vec3 (0.5 f,-0.5 f, 0.5 f), //right side
glm::vec3 (0.5 f,-0.5 f,-0.5 f),
glm::vec3 (0 .0F, 0.5 f, 0 .0F),
glm::vec3 (-0.5 f,-0.5 f, 0.5 f), //front side
glm::vec3 (0.5 f,-0.5 f, 0.5 f),
glm::vec3 (0 .0F, 0.5 f, 0 .0F),
glm::vec3 (0.5 f,-0.5 f,-0.5 f), //back side
glm::vec3 (-0.5 f,-0.5 f,-0.5 f),
glm::vec3 (0 .0F, 0.5 f, 0 .0F)};
Jak widzimy, podstawa (ang. basis) składa się z dwóch trójkątów (kwadrat), dlatego ma zdefiniowanych aż 6 wierzchołków. Natomiast wszystkie ścianki boczne są zwykłymi trójkątami, stąd 3 wierzchołki na każdą ściankę. Polecam narysowanie tego na kartce w zwykłym układzie kartezjańskim (OpenGL stosuje układ prawoskrętny - oś Z “wychodzi” z ekranu monitora). Warto zwrócić uwagę na kolejność podawania wierzchołków - są podawane w kolejności przeciwnej do ruchu wskazówek zegara (ang. counter clock wise). Jest tak dlatego, że OpenGL domyślnie ma ustawione, żeby uznawać takie wielokąty za te, które są “odwrócone” do wirtualnej kamery przodem (tylne ścianki nie są renderowane w celu optymalizacji - culling). Jeżeli chcemy by OpenGL traktował wielokąty o wierzchołkach, które są w kolejności zgodnej z ruchem wskazówek zegara (ang. clock wise) musimy wywołać funkcję glFrontFace(GLenum mode) z parametrem GL_CW.
Uaktualnijmy jeszcze wywołanie glDrawArrays() w funkcji render(), by OpenGL rysował dobrą ilość wierzchołków:
/* Draw our object */
glDrawArrays(GL_TRIANGLES, 0, 3*6);
Kolejne zmiany nastąpiły w funkcji int loadContent():
/* Set the world matrix to the identity matrix */
glm::mat4 world = glm::mat4 (1 .0F);
/* Set the view matrix */
glm::mat4 view = glm::lookAt (glm::vec3 (1.5 f 0.0 f, 1.5 f), //camera position in world space
glm::vec3 (0 .0F, 0 .0F, 0 .0F), //at this point the camera is looking at
glm::vec3 (0 .0F, 1 .0F, 0 .0F)); //the head is up
/* Set the projection matrix */
int w;
int h;
glfwGetWindowSize (window, &w, &h);
glm::mat4 projection = glm::perspective (45.0f, (float)w/(float)h, 0.001f, 50.0f);
/* Set MVP matrix */
glm::mat4 WVP = projection * view * world;
/* Get the uniform location and send MVP matrix there */
GLuint wvpLoc = glGetUniformLocation(programHandle, "wvp");
glUniformMatrix4fv(wvpLoc, 1, GL_FALSE, &WVP[0][0]);
W linijce #2 zaczynamy od zdefiniowania macierzy świata dla naszej piramidy. Konstruktor glm::mat4(1.0f) tworzy nam macierz jednostkową (na przekątnej ma jedynki, a reszta to zera). Ma ona tę właściwość, że kiedy pomnożymy macierz jednostkową przez macierz B to w wyniku dostaniemy niezmienioną macierz B.
W #5 linijce tworzymy macierz widoku (kamery). Funkcja glm::lookAt(…), przyjmuje trzy wektory. Pierwszy z nich to pozycja kamery w świecie. Drugi z nich to punkt w świecie na jaki patrzy kamera. Trzeci wektor mówi nam o tym czy trzymamy “głowę” prosto czy nie - jeżeli trzymamy prosto (najczęstszy przypadek) to ustawiamy wartość (0, 1, 0). Natomiast jeżeli ustawimy wartość (0, -1, 0) to będziemy oglądali scenę do góry nogami.
W linijce #12 pobieramy szerokość i wysokość okna OpenGL, by potem użyć tego w linijce #14 do stworzenia macierzy projekcji. Pierwszy parametr funkcji glm::perspective(…) to kąt widzenia w stopniach (z reguły jest to wartość z przedziału (0, 180) stopni). Drugi parametr to stosunek szerokości okna do jego wysokości (ang. aspect ratio). Dwa definiują dwie płaszczyzny widoku - bliską i daleką (na osi Z). Obiekty, które znajdują się poza obszarem zdefiniowanym przez te dwie płaszczyzny nie będą renderowane.
W linijce #17 tworzymy macierz WVP ze wszystkimi transformacjami, by później wysłać ją do shader’a i przekształcić nasz obiekt z układu lokalnego do układu ekranu. Jak widzimy kolejność mnożenia jest odwrotna - pierwsza transformacja jaką chcemy wykonać zawsze będzie na końcu, a ostatnia na początku.
Na koniec w linijce #20 używamy funkcji glGetUniformLocation(…) do uzyskania lokalizacji zmiennej, która jest zdefiniowana w programie cieniującym. Ta funkcja przyjmuje dwa parametry - uchwyt do programu, w którym są nasze shader’y, oraz ciąg znaków - nazwę naszej zmiennej w programie cieniującym. Ta lokalizacja jest nam potrzebna do funkcji w linijce #21 glUniformMatrix4fv(), która służy do wysłania macierzy 4x4 z CPU do GPU. Pierwszy parametr tej funkcji to lokalizacja naszej zmiennej, drugi to ilość macierzy jakie wysyłamy (możemy również wysłać tablicę macierzy), trzeci parametr “pyta” nas czy chcemy by wysyłaną macierz transponować czy nie, a czwarty parametr to wartość - czyli nasz macierz a dokładnie jej adres do pierwszego elementu. Zmienna programHandle została przeniesiona do globalnego zakresu (można to zauważyć w poprzednim listingu).
Przejdźmy teraz do omówienia vertex shader’a:
#version 440
layout (location = 0) in vec3 vertexPosition;
out vec3 pos;
uniform mat4 wvp;
void main()
{
pos = vertexPosition;
gl_Position = wvp * vec4(vertexPosition, 1.0f);
}
Jedyne zmiany jakie zaszły od poprzedniej części tutorialu są w linijce #7 i #13. W pierwszej z nich definiujemy zmienną uniform o typie mat4 (macierz 4x4), która nazywa się wvp. Kwalifikator uniform pozwala nam na przesyłanie danych do shader’a tak jak kwalifikator in. Jedyna różnica między tymi dwoma kwalifikatorami jest taka, że zmienna uniform nie zmienia swojej wartości w trakcie wywoływania kodu shader’a dla poszczególnych wierzchołków/fragmentów w ramach renderowania jednej ramki (jedno wywołanie funkcji render).
W linijce #13 przekształcamy, za pomocą macierzy wvp, pozycję wierzchołka od razu do współrzędnych ekranu.
Kiedy uruchomimy nasz program naszym oczom ukaże się oto taki widok:
Coś tu nie gra, prawda? Dzieje się tak dlatego, że jedna z tylnych ścianek została narysowana po tym jak została narysowana przednia ścianka, która miała zasłonić tą tylną. Jak to naprawić? Z pomocą przychodzi nam test głębi! Dzięki niemu OpenGL będzie mógł zadecydować, który wielokąt przesłania, który by dobrze to wszystko narysować. W tym celu w funkcji init() umieszczamy instrukcję:
/* Enable depth test */
glEnable(GL_DEPTH_TEST);
Włączy nam ona test głębi i będzie zapisywać do bufora głębi różne dane. Niestety to nie wszystko. W funkcji render() przed namalowaniem całej sceny musimy jeszcze czyścić bufor głębi. W tym celu uaktualniamy wywołanie funkcji glClear(…):
/* Clear the color buffer & depth buffer*/
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
Wykonujemy tutaj logiczną operację OR na dwóch wartościach, przez co OpenGL będzie wiedział by czyścić zarówno bufor koloru jak i bufor głębi.
Efekt końcowy można zobaczyć poniżej:
Zakończenie
To już koniec tej części kursu. Jak zwykle - gdyby było coś nie jasne proszę pisać komentarze pod spodem lub kontaktować się ze mną mailowo. Zapraszam na kolejną część, w której zapoznamy się z transformacjami w świecie 3D - będzie w końcu trochę ruchu! :-)