This is the Polish translation of Getting-started/Transformations article of learnopengl.com tutorial series.

Wiemy już, jak tworzyć obiekty, kolorować je i / lub nadawać im szczegółowy wygląd przy użyciu tekstur, ale wciąż nie są one interesujące, ponieważ są to statyczne obiekty. Moglibyśmy spróbować zmusić je do ruchu, zmieniając ich wierzchołki i ponownie konfigurując ich bufory w każdej ramce, ale jest to kłopotliwe i kosztuje trochę mocy obliczeniowej. Istnieje wiele lepszych sposobów transformowania obiektu, przy użyciu (kilku) macierzy. To nie oznacza, że będziemy rozmawiać o kung-fu i dużym cyfrowym, sztucznym świecie.

Macierze są bardzo potężnymi konstrukcjami matematycznymi, które wydają się na początku straszne, ale gdy już się do nich przyzwyczaisz, okażą się bardzo przydatnym narzędziem. Podczas opowieści o macierzach, musimy trochę zagłębić się w pewnej matematyce. Dla czytelników bardziej skupionych na matematyce dołączę dodatkowe materiały do dalszej lektury.

Aby jednak w pełni zrozumieć transformacje musimy najpierw zgłębić wektory, przed mówieniem o macierzach. Celem tego rozdziału jest dostarczenie podstawowego matematycznego tła w kwestiach, których będziemy potrzebować później. Jeśli tematy są trudne, spróbuj zrozumieć je w jak największym stopniu, jak to tylko możliwe i wróć do tej strony później, aby przypomnieć sobie pewne rzeczy, jak będziesz ich potrzebował.

Wektory

W najbardziej podstawowej definicji wektory są kierunkami i niczym więcej. Wektor ma kierunek i wielkość (znany również jako jego siła lub długość). Możesz postrzegać wektory, jako wskazówki na mapie skarbów: “idź 10 kroków w lewo, a następnie idź 3 kroki na północ i idź 5 kroków w prawo”; w tym przykładzie ‘lewo’ oznacza kierunek, a ‘10 kroków’ jest wielkością wektora. Wskazówki mapy skarbów zawierają zatem 3 wektory. Wektory mogą mieć dowolny wymiar, ale zwykle pracujemy z wymiarami od 2 do 4. Jeśli wektor ma 2 wymiary, to reprezentuje kierunek na płaszczyźnie (wykresy 2D), a gdy ma 3 wymiary, to może reprezentować dowolny kierunek w świecie 3D.

Poniżej możesz zobaczyć 3 wektory, gdzie każdy wektor jest reprezentowany przez (x, y) jako strzałki na wykresie 2D. Ponieważ bardziej intuicyjne jest wyświetlanie wektorów w 2D (niż w 3D), można myśleć o wektorach 2D jako wektorach 3D o współrzędnej z równej 0. Ponieważ wektory reprezentują kierunki, początek wektora nie zmienia jego wartości. Na poniższym wykresie widać, że wektory $\color{red}{\bar{v}}$ i $\color{blue}{\bar{w}}$ są równe, mimo że ich punkty początkowe są inne:

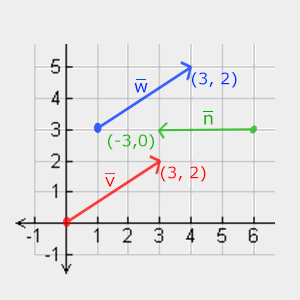
Matematycy opisując wektory, oznaczają je literką z małym daszkiem u góry jak np. $\bar{v}$. Również, gdy wektory są pokazywane we wzorach, to są ogólnie pokazywane w następujący sposób:

\[\bar{v} = \begin{pmatrix} \color{red}x \\ \color{green}y \\ \color{blue}z \end{pmatrix}\]

Ponieważ wektory określają kierunki, to czasami trudno je zwizualizować jako pozycje. Aby jednak to zrobić, to ustawiamy początek wektora na (0,0,0), a następnie ustawiamy jego koniec na punkcie, który chcemy zdefiniować. W ten sposób tworzymy wektor pozycji (możemy też określić inny początek wektora, a następnie powiedzieć: “ten wektor wskazuje na ten punkt w przestrzeni, z tego punktu początkowego”). Wektor położenia (3,5) wskazywałby na punkt (3,5) na wykresie, o początku (0,0) . Korzystając z wektorów możemy opisywać kierunki ipozycje w przestrzeni 2D i 3D.

Podobnie jak w przypadku normalnych liczb, możemy zdefiniować kilka operacji na wektorach (niektóre z nich już widziałeś).

Skalarne operacje na wektorach

Skalar jest pojedynczą cyfrą (lub wektorem zawierającym jeden składnik, jeśli chcesz pozostać w obszarze wektora). Dodając/odejmując/mnożąc lub dzieląc wektor przez skalar, po prostu dodajesz/odejmujesz/mnożysz lub dzielisz każdy element wektora przez ten skalar. Wyglądałoby to tak:

\[\begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix} + x = \begin{pmatrix} \color{red}{1} + x \\ \color{green}{2} + x \\ \color{blue}{3} + x \end{pmatrix}\]

Gdzie $+$ może być $+$, $-$, $\cdot$ lub $\div$, gdzie $\cdot$ jest operatorem mnożenia. Należy pamiętać, że dla operatorów $-$ i $\div$ odwrotna kolejność działań nie jest zdefiniowana.

Negowanie (odwracanie) wektora

Negowanie wektora daje w wyniku wektor o przeciwnym kierunku. Wektor, wskazując północny wschód, wskazywałby na południowy zachód po negacji. Aby zanegować wektor, dodajemy znak minus do każdego składnika (można to również przedstawić jako mnożenie wektora z wartością skalarną -1):

\[-\bar{v} = -\begin{pmatrix} \color{red}{v_x} \\ \color{blue}{v_y} \\ \color{green}{v_z} \end{pmatrix} = \begin{pmatrix} -\color{red}{v_x} \\ -\color{blue}{v_y} \\ -\color{green}{v_z} \end{pmatrix}\]

Dodawanie i odejmowanie

Dodawanie dwóch wektorów definiuje się jako dodawanie do siebie odpowiadających sobie składników wektora, czyli każdy składnik jednego wektora dodaje się do tego samego składnika innego wektora, np.:

\[\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + \bar{k} = \begin{pmatrix} \color{red}1 + \color{red}4 \\ \color{green}2 + \color{green}5 \\ \color{blue}3 + \color{blue}6 \end{pmatrix} = \begin{pmatrix} \color{red}5 \\ \color{green}7 \\ \color{blue}9 \end{pmatrix}\]

Na obrazku wygląda to tak, dla wektorów v=(4,2) i k=(1,2):

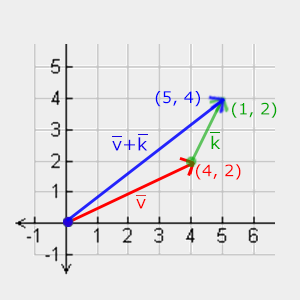
Podobnie jak w przypadku normalnego dodawania i odejmowania, odejmowanie wektorów jest takie samo jak dodawanie jednego wektora z zanegowanym drugim wektorem:

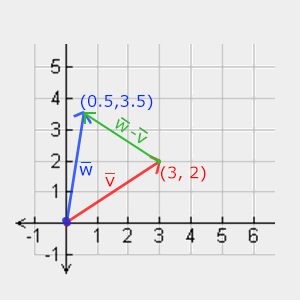
\[\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + -\bar{k} = \begin{pmatrix} \color{red}1 + (-\color{red}{4}) \\ \color{green}2 + (-\color{green}{5}) \\ \color{blue}3 + (-\color{blue}{6}) \end{pmatrix} = \begin{pmatrix} -\color{red}{3} \\ -\color{green}{3} \\ -\color{blue}{3} \end{pmatrix}\]

Odejmowanie dwóch wektorów od siebie powoduje powstanie wektora, który jest różnicą pozycji, na którą wskazują wektory. Jest to przydatne w niektórych przypadkach, gdy musimy pobrać wektor, który jest różnicą między dwoma punktami.

Długość

Aby pobrać długość/wielkość wektora używamy twierdzenia Pitagorasa, które możesz pamiętać z lekcji matematyki. Wektor tworzy trójkąt, gdy zwizualizujesz jego poszczególne składniki x i y jako dwa boki trójkąta:

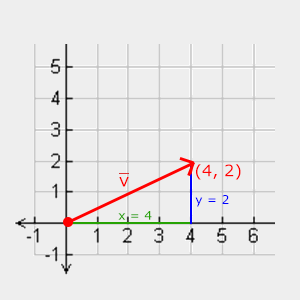
Ponieważ długości obu boków (x, y) są znane i chcemy wiedzieć jaka jest długość nachylonego boku $\color{red}{\bar{v}}$, to możemy ją obliczyć przy użyciu twierdzenia Pitagorasa:

\[||\color{red}{\bar{v}}|| = \sqrt{\color{green}x^2 + \color{blue}y^2}\]

Gdzie $\lvert\lvert\color{red}{\bar{v}}\rvert\rvert$ oznacza długość wektora $\color{red}{\bar{v}}$. Można to łatwo rozszerzyć do 3D, dodając $z^2$ do równania.

W tym przypadku długość wektora (4, 2) jest równa 4.47:

\[||\color{red}{\bar{v}}|| = \sqrt{\color{green}4^2 + \color{blue}2^2} = \sqrt{\color{green}16 + \color{blue}4} = \sqrt{20} = 4.47\]

Istnieje również specjalny typ wektora, który nazywamy wektorem jednostkowym. Wektor jednostkowy ma jedną dodatkową właściwość - jego długość jest równa dokładnie 1. Możemy stworzyć wektor jednostkowy $\hat{n}$ z dowolnego wektora, dzieląc każdy ze składników wektora przez jego długość:

\[\hat{n} = \frac{\bar{v}}{||\bar{v}||}\]

Nazywamy to normalizowaniem wektora. Wektory jednostkowe są oznaczane małym daszkiem i są z reguły łatwiejsze w obsłudze, szczególnie gdy interesują nas tylko ich kierunki (kierunek nie zmienia się, jeśli zmieniamy długość wektora).

Mnożenie wektora przez wektor

Mnożenie dwóch wektorów jest trochę dziwne. Zwykłe mnożenie wektorów nie jest zdefiniowane, ponieważ nie ma żadnego geometrycznego znaczenia, dlatego mamy dwa konkretne warianty, które możemy wybrać podczas mnożenia: jeden to iloczyn skalarny (ang. dot product) oznaczanym jako $\bar{v} \cdot \bar{k}$, a drugi to iloczyn wektorowy (ang. cross product) oznaczany jako $\bar{v} \times \bar{k}$.

Iloczyn skalarny

Iloczyn skalarny dwóch wektorów jest równy iloczynowi ich długości oraz kąta między nimi. Jeśli to brzmi niejasno spójrz na poniższy wzór:

\[\bar{v} \cdot \bar{k} = ||\bar{v}|| \cdot ||\bar{k}|| \cdot \cos \theta\]

Gdzie kąt między nimi jest reprezentowany jako theta $(\theta)$. Dlaczego to działanie jest interesujące? Cóż, wyobraź sobie, że jeśli $\bar{v}$ i $\bar{k}$ są wektorami jednostkowymi, to ich długość będzie równa 1. To skutecznie redukuje wzór do postaci:

\[\bar{v} \cdot \bar{k} = 1 \cdot 1 \cdot \cos \theta = \cos \theta\]

Teraz iloczyn skalarny definiuje tylko kąt pomiędzy dwoma wektorami. Możesz zauważyć, że cosinus lub funkcja cos jest równa 0, gdy kąt jest równy 90 stopni, lub 1, gdy kąt jest równy 0var> stopni. Pozwala to łatwo sprawdzić, czy dwa wektory są prostopadłe lub równolegle w stosunku do siebie. W przypadku, gdy chcesz dowiedzieć się więcej na temat funkcji trygonometrycznych sugeruję zapoznać się z filmami Khan Academy.

Możesz również obliczyć kąt pomiędzy dwoma wektorami nie będącymi wektorami jednostkowymi, ale wtedy musisz podzielić długości obu wektorów z wyniku, który pozostanie wraz z $cos \theta$.

Jak obliczyć iloczyn skalarny? Iloczyn skalarny jest mnożeniem odpowiadających sobie komponentów, gdzie później dodajemy do siebie wszystkie wyniki. Wygląda to tak, jak w przypadku dwóch wektorów jednostkowych (można sprawdzić, czy długości obu wektorów są równe 1):

\[\begin{pmatrix} \color{red}{0.6} \\ -\color{green}{0.8} \\ \color{blue}0 \end{pmatrix} \cdot \begin{pmatrix} \color{red}0 \\ \color{green}1 \\ \color{blue}0 \end{pmatrix} = (\color{red}{0.6} * \color{red}0) + (-\color{green}{0.8} * \color{green}1) + (\color{blue}0 * \color{blue}0) = -0.8\]

Aby obliczyć kąt między obydwoma wektorami jednostkowymi, używamy odwrotności funkcji cosinus $cos^{-1}$, co prowadzi do kąta równego 143.1 stopni. Teraz sprawnie obliczyliśmy kąt między tymi dwoma wektorami. Iloczyn skalarny jest bardzo przydatny przy obliczaniu oświetlenia.

Iloczyn wektorowy

Iloczyn wektorowy jest zdefiniowany tylko w przestrzeni 3D i przyjmuje na wejściu dwa nie równoległe wektory i jego wynikiem jest trzeci wektor, który jest prostopadły do obu wektorów wejściowych. Jeśli oba wektory wejściowe są prostopadłe względem siebie, to iloczyn wektorowy zwróciłby trzeci wektor prostopadły. To narzędzie będzie przydatne w kolejnych tutorialach. Poniższy obrazek pokazuje, jak wygląda to w przestrzeni 3D:

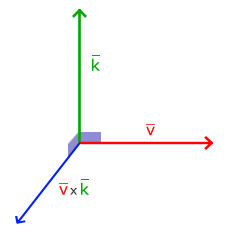
W przeciwieństwie do innych operacji, iloczyn wektorowy nie jest zbyt intuicyjny, bez zaangażowania się w algebrę liniową, najlepiej więc zapamiętać formułę i wszystko bedzie w porządku (lub nie zapamiętuj, w obu przypadkach będzie w miarę dobrze). Poniżej możesz zobaczyć iloczyn wektorowy pomiędzy dwoma prostopadłymi wektorami A i B:

\[\begin{pmatrix} \color{red}{A_{x}} \\ \color{green}{A_{y}} \\ \color{blue}{A_{z}} \end{pmatrix} \times \begin{pmatrix} \color{red}{B_{x}} \\ \color{green}{B_{y}} \\ \color{blue}{B_{z}} \end{pmatrix} = \begin{pmatrix} \color{green}{A_{y}} \cdot \color{blue}{B_{z}} - \color{blue}{A_{z}} \cdot \color{green}{B_{y}} \\ \color{blue}{A_{z}} \cdot \color{red}{B_{x}} - \color{red}{A_{x}} \cdot \color{blue}{B_{z}} \\ \color{red}{A_{x}} \cdot \color{green}{B_{y}} - \color{green}{A_{y}} \cdot \color{red}{B_{x}} \end{pmatrix}\]

Jak widać, na pierwszy rzut oka nie ma to działanie sensu. Jeśli jednak wykonasz te czynności, otrzymasz inny wektor, który jest prostopadły do wektorów wejściowych.

Macierze

Teraz, gdy omówiliśmy już prawie wszystko, co dotyczy wektorów, nadszedł czas, aby przejść do macierzy! Macierz jest w zasadzie prostokątną tablicą liczb, symboli i/lub wyrażeń. Każda pojedyncza pozycja w macierzy jest nazywana elementem macierzy. Przykład macierzy 2x3 jest pokazany poniżej:

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\]

Macierze są indeksowane przez parę (i, j) gdzie i odpowiada wierszowi, a j odpowiada kolumnie. Dlatego powyższa macierz jest nazywana macierzą 2x3 (3 kolumny i 2 wiersze, znany również jako wymiar macierzy). Jest to przeciwieństwo tego, do czego się przyzwyczaiłeś podczas indeksowania wykresów 2D jako para (x, y). Aby pobrać wartość 4, indeksowalibyśmy ją jako (2,1) (drugi wiersz, pierwsza kolumna).

Macierze są w zasadzie niczym więcej, jak prostokątnymi tablicami wyrażeń matematycznych. Mają bardzo ciekawy zestaw właściwości matematycznych i podobnie jak wektory możemy zdefiniować kilka operacji na macierzach, a mianowicie: dodawanie, odejmowanie i mnożenie.

Dodawanie i odejmowanie

Dodawanie i odejmowanie między macierzą a skalarem jest definiowane w następujący sposób:

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \color{green}3 = \begin{bmatrix} 1 + \color{green}3 & 2 + \color{green}3 \\ 3 + \color{green}3 & 4 + \color{green}3 \end{bmatrix} = \begin{bmatrix} 4 & 5 \\ 6 & 7 \end{bmatrix}\]

Wartość skalarna jest zasadniczo dodawana do każdego pojedynczego elementu macierzy. To samo tyczy się odejmowania skalara od macierzy:

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} - \color{green}3 = \begin{bmatrix} 1 - \color{green}3 & 2 - \color{green}3 \\ 3 - \color{green}3 & 4 - \color{green}3 \end{bmatrix} = \begin{bmatrix} -2 & -1 \\ 0 & 1 \end{bmatrix}\]

Dodawanie i odejmowanie dwóch macierzy odbywa się na zasadzie element po elemencie. Tak więc, obowiązują te same ogólne zasady, które znamy dla normalnych liczb, ale wykonywanych na elementach obu macierzy z tym samym indeksem. Oznacza to, że dodawanie i odejmowanie jest zdefiniowane tylko dla macierzy o tych samych wymiarach. Nie można dodawać ani odejmować macierzy 3x2 i macierzy 2x3 (lub macierzy 3x3 i macierzy 4x4). Przyjrzyjmy się, jak dodawanie działa na dwóch macierzach 2x2:

\[\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} + \begin{bmatrix} \color{red}5 & \color{red}6 \\ \color{green}7 & \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 + \color{red}5 & \color{red}2 + \color{red}6 \\ \color{green}3 + \color{green}7 & \color{green}4 + \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}6 & \color{red}8 \\ \color{green}{10} & \color{green}{12} \end{bmatrix}\]

Te same reguły mają zastosowanie przy odejmowaniu macierzy:

\[\begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2 - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}\]

Mnożenie macierzy przez skalar

Podobnie jak dodawanie i odejmowanie, mnożenie skalara przez macierz odbywa się przez przemnożenie każdego elementu macierzy przez liczbę. Poniższy przykład ilustruje mnożenie:

\[\color{green}2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} \color{green}{2} \cdot 1 & \color{green}{2} \cdot 2 \\ \color{green}{2} \cdot 3 & \color{green}{2} \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}\]

Teraz ma również sens, dlaczego te pojedyncze liczby są nazywane skalarami. Skalar w zasadzie skaluje wszystkie elementy macierzy przez jego wartość. W poprzednim przykładzie wszystkie elementy były skalowane przez 2.

Na razie, wszystkie operacje nie były zbyt skomplikowane. To znaczy, że teraz zaczniemy mnożenie macierzowe.

Mnożenie macierzy

Mnożenie macierzy nie jest samo w sobie trudne. Trudnością jest oswojenie się z nim. Mnożenie macierzy zasadniczo oznacza, stosowanie się do predefiniowanych reguł. Istnieje jednak kilka ograniczeń:

1. Można pomnożyć dwie macierze, jeśli liczba kolumn lewej macierzy jest równa liczbie wierszy z macierzy po prawej stronie.
2. Mnożenie macierzy nie jest przemienne czyli $A \cdot B \neq B \cdot A$.

Zacznijmy od przykładu mnożenia dwóch macierzy 2x2:

\[\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} \cdot \begin{bmatrix} \color{blue}5 & \color{purple}6 \\ \color{blue}7 & \color{purple}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot \color{blue}5 + \color{red}2 \cdot \color{blue}7 & \color{red}1 \cdot \color{purple}6 + \color{red}2 \cdot \color{purple}8 \\ \color{green}3 \cdot \color{blue}5 + \color{green}4 \cdot \color{blue}7 & \color{green}3 \cdot \color{purple}6 + \color{green}4 \cdot \color{purple}8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}\]

W tej chwili prawdopodobnie próbujesz dowiedzieć się, co się tutaj właściwie wyprawia? Mnożenie macierzy jest połączeniem normalnego mnożenia i dodawania za pomocą wierszy lewej macierzy z kolumnami prawej macierzy. Spróbujmy wyjaśnić to za pomocą obrazu:

Bierzemy najpierw górny wiersz lewej macierzy i pierwszą kolumnę z prawej macierzy. Wybrany wiersz i kolumna decyduje, którą wartość wyjściową otrzymanej matrycy 2x2 będziemy obliczać. Jeśli weźmiemy pierwszy wiersz lewej macierzy, to otrzymana wartość zostanie zapisana w pierwszym wierszu wynikowej macierzy. Następnie wybieramy kolumnę i jeśli jest to pierwsza kolumna, wartość wyniku zostanie wpisana w pierwszej kolumnie wynikowej macierzy. To jest dokładnie przypadek oznaczony czerwonym obramowaniem. Aby obliczyć prawy dolny wynik, bierzemy dolny wiersz pierwszej macierzy i prawą kolumnę drugiej macierzy.

Aby obliczyć wynikową wartość, mnożymy pierwszy element wiersza i kolumny używając normalnego mnożenia. Wykonujemy to samo dla drugiego elementu, trzeciego, czwartego itp. Wyniki poszczególnych mnożeń są następnie sumowane ze sobą i otrzymujemy wynik. Teraz ma również sens, to że jednym z wymagań jest to, że liczba kolumn lewej macierzy i liczba wierszy prawej macierzy muszą być równe, w przeciwnym razie nie moglibyśmy zakończyć operacji!

Wynikiem jest wtedy macierz o wymiarach (n, m), gdzie n jest równe liczbie wierszy macierzy po lewej stronie, a m jest równe liczbie kolumn macierzy po prawej stronie działania.

Nie martw się, jeśli masz problemy z wyobrażaniem sobie mnożenia w pamięci. Po prostu staraj się wykonywać obliczenia ręcznie i wróć do tej strony, gdy będziesz miał problemy. W miarę upływu czasu mnożenie macierzy stanie się dla Ciebie drugą naturą.

Zakończmy dyskusję na temat mnożenia macierzy większym przykładem. Spróbuj wyobrazić sobie schemat działania za pomocą kolorów. Jako ćwiczenie sprawdź, czy potrafisz samemu wykonać mnożenie poniższych macierzy, aby następnie porównać Twoją odpowiedź z wynikiem na tej stronie (kiedy wykonasz mnożenie macierzy ręcznie, szybciej je zrozumiesz).

\[\begin{bmatrix} \color{red}4 & \color{red}2 & \color{red}0 \\ \color{green}0 & \color{green}8 & \color{green}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \end{bmatrix} \cdot \begin{bmatrix} \color{red}4 & \color{green}2 & \color{blue}1 \\ \color{red}2 & \color{green}0 & \color{blue}4 \\ \color{red}9 & \color{green}4 & \color{blue}2 \end{bmatrix} = \begin{bmatrix} \color{red}4 \cdot \color{red}4 + \color{red}2 \cdot \color{red}2 + \color{red}0 \cdot \color{red}9 & \color{red}4 \cdot \color{green}2 + \color{red}2 \cdot \color{green}0 + \color{red}0 \cdot \color{green}4 & \color{red}4 \cdot \color{blue}1 + \color{red}2 \cdot \color{blue}4 + \color{red}0 \cdot \color{blue}2 \\ \color{green}0 \cdot \color{red}4 + \color{green}8 \cdot \color{red}2 + \color{green}1 \cdot \color{red}9 & \color{green}0 \cdot \color{green}2 + \color{green}8 \cdot \color{green}0 + \color{green}1 \cdot \color{green}4 & \color{green}0 \cdot \color{blue}1 + \color{green}8 \cdot \color{blue}4 + \color{green}1 \cdot \color{blue}2 \\ \color{blue}0 \cdot \color{red}4 + \color{blue}1 \cdot \color{red}2 + \color{blue}0 \cdot \color{red}9 & \color{blue}0 \cdot \color{green}2 + \color{blue}1 \cdot \color{green}0 + \color{blue}0 \cdot \color{green}4 & \color{blue}0 \cdot \color{blue}1 + \color{blue}1 \cdot \color{blue}4 + \color{blue}0 \cdot \color{blue}2 \end{bmatrix} \\ = \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}\]

Jak widać, mnożenie macierzy jest dość kłopotliwe i bardzo podatne na błędy (dlatego zwykle pozwalamy robić to komputerom) i to staje się szybko problematyczne, gdy macierze stają się większe. Jeśli nadal jesteś spragniony wiedzy i jesteś ciekawy niektórych matematycznych właściwości macierzy, zdecydowanie polecam obejrzeć filmy Khan Academy o macierzach.

W każdym razie, skoro wiemy, jak mnożyć dwie macierze, możemy przejść do ciekawszych rzeczy.

Mnożenie wektora przez macierz

Do tej pory mieliśmy dosyć dużo doczynienia z wektorami. Używaliśmy ich do reprezentowania pozycji, kolorów i nawet współrzędnych tekstur. Idźmy trochę dalej i powiedzmy, że wektor jest w zasadzie macierzą Nx1, gdzie N jest liczbą elementów wektora (znanym również jako N-wymiarowym). Jeśli pomyślisz o tym, to ma to wiele sensu. Wektory są, tak jak macierze, tablicą liczb, ale tylko z 1 kolumną. W jaki sposób to nowe spojrzenie na wektory może nam pomóc? Cóż, jeśli mamy macierz MxN, możemy ją pomnożyć przez nasz wektor Nx1, ponieważ kolumny naszej macierzy są równe liczbie wierszy naszego wektora, więc mnożenie macierzy będzie poprawne.

Ale dlaczego obchodzi nas, czy możemy pomnożyć wektor przez macierz? Cóż, tak się składa, że istnieje wiele interesujących przekształceń 2D/3D, które można umieścić wewnątrz macierzy i mnożąc tę macierz przez nasz wektor, to zasadniczo przekształcamy nasz wektor. Jeśli nadal jesteś trochę zdezorientowany, zacznijmy od kilku przykładów, a wkrótce zobaczysz, co mam na myśli.

Macierz jednostkowa

W OpenGL zazwyczaj pracujemy z macierzami transformacji 4x4 z kilku powodów, a jeden z nich to, to że większość wektorów ma rozmiar 4. Najbardziej podstawową macierzą transformacji, o której możemy pomyśleć, jest macierz jednostkowa (ang. identity matrix). Macierz jednostkowa jest macierzą NxN z samymi wartościami 0, z wyjątkiem przekątnej tej macierzy, na której są wartości 1. Jak zobaczysz, ta macierz transformacji nie przekształca wektora w żaden sposób:

\[\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot 1 \\ \color{green}1 \cdot 2 \\ \color{blue}1 \cdot 3 \\ \color{purple}1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}\]

Wektor wydaje się zupełnie nietknięty. Wynika to z reguły mnożenia: pierwszym elementem wyniku jest każdy indywidualny element pierwszego wiersza macierzy pomnożony przez każdy element wektora. Ponieważ każdy z elementów wiersza jest 0 z wyjątkiem pierwszego, to otrzymujemy: $\color{red}{1}\cdot1 + \color{red}{0}\cdot2 + \color{red}{0}\cdot3 + \color{red}{0}\cdot4 = 1$ i to samo dotyczy pozostałych 3 elementów wektora.

Być może zastanawiasz się, jakie jest zastosowanie macierzy jednostkowej, która nic nie zmienia? Macierz jednostkowa jest zwykle punktem wyjścia do generowania innych macierzy transformacji i jeśli będziemy zagłębiać się jeszcze głębiej w algebrę liniową, bardzo to ta macierz jest bardzo użyteczną macierzą dla udowadniania twierdzeń i rozwiązywania równań liniowych.

Skalowanie

Kiedy skalujemy wektor, zwiększamy jego długość o wartość, którą chcemy skalować, zachowując kierunek wektora. Ponieważ pracujemy w dwóch lub trzech wymiarach, możemy zdefiniować skalowanie przez 2 lub 3 zmienne skalowania, przy czym każda zmienna skaluje jedną oś (x, y lub z) .

Spróbujmy przeskalować wektor $\color{red}{\bar{v}} = (3,2)$. Przeskalujemy ten wektor wzdłuż osi x przez wartość 0.5, co zmniejszy nam wektor dwukrotnie (w osi x). Również, przeskalujemy ten wektor przez wartość 2 wzdłuż osi y, co powiększy go dwukrotnie (w osi y). Przyjrzyjmy się, jak to wygląda, jeśli przeskalujemy nasz wektor przez wektor (0.5, 2) oznaczony jako $\color{blue}{\bar{s}}$:

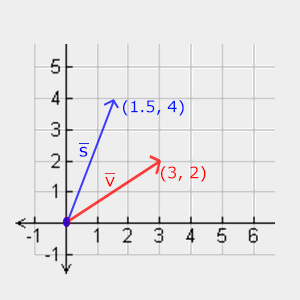
Należy pamiętać, że OpenGL zazwyczaj działa w przestrzeni 3D, więc w przypadku 2D możemy ustawić skalowanie osi z na wartość 1, pozostawiając ją bez zmian. Operacja skalowania, którą właśnie przeprowadziliśmy, jest skalą nierównomierną (ang. non-uniform scale), ponieważ współczynnik skalowania nie jest taki sam dla każdej osi. Jeśli skalar byłby ten sam na wszystkich osiach, nazywałby się skalą równomierną (ang. uniform scale).

Zacznijmy od budowy macierzy transformacji, która będzie skalować. Widzieliśmy przy omawianiu macierzy jednostkowej, że każdy element leżący na przekątnej został pomnożony przez odpowiadający jej element wektora. Co się stanie jeśli zmienimy 1 w macierzy jednostkowej na 3? W takim przypadku mnożymy każdy element wektora przez wartość 3, a tym samym efektywnie przeskalujemy wektor przez 3. Oznaczmy zmienne skalowania jako $(\color{red}{S_1}, \color{green}{S_2}, \color{blue}{S_3})$ i zdefiniujmy macierz skalowania dowolnego wektora $(x,y,z)$ jako:

\[\begin{bmatrix} \color{red}{S_1} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{S_2} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}{S_3} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{S_1} \cdot x \\ \color{green}{S_2} \cdot y \\ \color{blue}{S_3} \cdot z \\ 1 \end{pmatrix}\]

Zauważ, że czwarty komponent wektor skalowania pozostaje 1, ponieważ nie jest to zdefiniowane, aby skalować składnik w w przestrzeni 3D. Składnik w jest używany do innych celów, ale zobaczymy to później.

Translacja

Translacja jest procesem dodawania innego wektora do oryginalnego wektora, aby zwrócić nowy wektor, ale w innej pozycji, a zatem jest to przenoszenie wektora na podstawie wektora translacji. Omówiliśmy już dodawanie wektorowe, więc nie powinno to być zbyt nowe.

Podobnie jak macierz skalowania, mamy kilka miejsc w macierzy 4x4, które możemy użyć do wykonywania pewnych operacji. Dla translacji są to 3 wartości od góry w czwartej kolumnie. Jeśli oznaczymy wektor translacji jako $(\color{red}{T_x},\color{green}{T_y},\color{blue}{T_z})$ to możemy zdefiniować macierz translacji jako:

\[\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}{T_x} \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}{T_y} \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}{T_z} \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + \color{red}{T_x} \\ y + \color{green}{T_y} \\ z + \color{blue}{T_z} \\ 1 \end{pmatrix}\]

To działa, ponieważ wszystkie wartości translacji są pomnożone przez kolumnę w i są później dodawane do oryginalnych wartości (pamiętaj o regułach mnożenia macierzy). To nie byłoby możliwe przy zastosowaniu macierzy 3x3.

Współrzędne jednorodne (ang. Homogeneous coordinates)
Element wektora w jest również znany jako współrzędna jednorodna. Aby uzyskać wektor 3D z wektora jednorodnego, dzielimy współrzędne x, y i z przez współrzędną w. Zazwyczaj nie zauważamy tego, ponieważ składnik w jest równy 1.0 przez większość czasu. Korzystanie z współrzędnych jednorodnych ma kilka zalet: umożliwia wykonywanie translacji na wektorach 3D (bez składnika w nie można wykonywać translacji na wektorach) i w następnym rozdziale będziemy używać wartości w do stworzenia wizualizacji 3D.

Ponadto, gdy tylko współrzędna jednorodna jest równa 0, wektor jest uznawany jako wektor kierunku (ang. direction vector), ponieważ wektor o współrzędnej w równej 0 nie może być przesuwany.

Dzięki macierzy translacji możemy przemieścić obiekty w dowolnym z trzech kierunków (x, y, z), dzięki czemu będzie to bardzo przydatne przekształcanie w naszym zestawie macierzy transformacji.

Rotacja

Ostatnie transformacje było stosunkowo łatwe do zrozumienia i zwizualizowania w przestrzeni 2D lub 3D, ale rotacja jest nieco trudniejsza. Jeśli chcesz dokładnie wiedzieć, w jaki sposób te macierze są zbudowane, zalecam, abyś obejrzał materiały Khan Academy algebry liniowej dotyczących rotacji.

Najpierw ustalmy, czym jest rotacja wektora. Obrót w 2D lub 3D jest reprezentowany za pomocą kąta . Kąt może być zapisany w stopniach lub radianach, gdzie całe koło ma 360 stopni lub 2 PI radianów. Osobiście wolę pracować w stopniach, ponieważ są dla mnie bardziej sensowne.

Większość funkcji rotacji wymaga kąta w radianach, ale na szczęście stopnie można łatwo przekształcić w radiany:
kąt w stopniach = kąt w radianach * (180.0f / PI)
kąt w radianach = kąt w stopniach * (PI / 180.0f)
Gdzie PI równa się (w przybliżeniu) 3.14159265359.

Obrót o półokręgu obróciłoby nas o 360/2 = 180 stopni, a obrót o 1/5 w prawo oznacza obrót o 360/5 = 72 stopnie w prawo. Jest to przedstawione dla prostego wektora 2D, w którym $\color{red}{\bar{v}}$ jest obrócone o 72 stopnie w prawo, w stosunku do pozycji wyjściowej \color{green}{\bar{k}}:

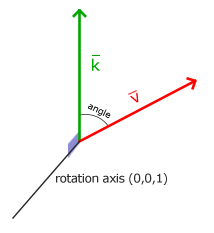
Rotacje w 3D są określone za pomocą kąta i osi obrotu . Określony kąt obróci przedmiot wzdłuż podanej osi obrotu. Spróbuj to sobie zobrazować, obracając głowę o pewien kąt, ciągle patrząc w dół na jedną oś obrotu. Podczas obracania wektorów 2D w świecie 3D ustawiamy, na przykład, oś obrotu na oś z (spróbuj to sobie zobrazować).

Wykorzystując trygonometrię można przekształcić wektory do nowych obróconych wektorów o podany kąt. Zwykle odbywa się to za pomocą inteligentnego połączenia funkcji sinus i cosinus (powszechnie określanych skrótami sin i cos) . Dyskusja o tym, jak generowane są te macierze transformacji, jest poza zakresem tego samouczka.

Macierz rotacji jest zdefiniowana dla każdej osi w przestrzeni 3D, gdzie kąt jest reprezentowany jako symbol theta $\theta$.

Rotacja wokół osi X:

\[\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{\cos \theta} & - \color{green}{\sin \theta} & \color{green}0 \\ \color{blue}0 & \color{blue}{\sin \theta} & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \color{green}{\cos \theta} \cdot y - \color{green}{\sin \theta} \cdot z \\ \color{blue}{\sin \theta} \cdot y + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}\]

Rotacja wokół osi Y:

\[\begin{bmatrix} \color{red}{\cos \theta} & \color{red}0 & \color{red}{\sin \theta} & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ - \color{blue}{\sin \theta} & \color{blue}0 & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x + \color{red}{\sin \theta} \cdot z \\ y \\ - \color{blue}{\sin \theta} \cdot x + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}\]

Rotacja wokół osi Z:

\[\begin{bmatrix} \color{red}{\cos \theta} & - \color{red}{\sin \theta} & \color{red}0 & \color{red}0 \\ \color{green}{\sin \theta} & \color{green}{\cos \theta} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x - \color{red}{\sin \theta} \cdot y \\ \color{green}{\sin \theta} \cdot x + \color{green}{\cos \theta} \cdot y \\ z \\ 1 \end{pmatrix}\]

Korzystając z macierzy rotacji możemy przekształcić nasze wektory pozycji wokół jednej z trzech osi. Możliwe jest również połączenie tych rotacji, najpierw obracając wokół osi X, a następnie na przykład wokół osi Y. Niestety, to szybko wprowadza problem zwany Gimbal lock. Nie będziemy omawiać szczegółów, ale lepszym rozwiązaniem byłoby obracanie wokół dowolnej osi, np. (0.662,0.2,0.722) (zauważ, że jest to wektor jednostkowy) od razu zamiast łączyć ze sobą macierze rotacji. Taka (paskudna) macierz istnieje i podana jest poniżej. $(\color{red}{R_x}, \color{green}{R_y}, \color{blue}{R_z})$ oznaczają dowolną oś obrotu:

\[\begin{bmatrix} \cos \theta + \color{red}{R_x}^2(1 - \cos \theta) & \color{red}{R_x}\color{green}{R_y}(1 - \cos \theta) - \color{blue}{R_z} \sin \theta & \color{red}{R_x}\color{blue}{R_z}(1 - \cos \theta) + \color{green}{R_y} \sin \theta & 0 \\ \color{green}{R_y}\color{red}{R_x} (1 - \cos \theta) + \color{blue}{R_z} \sin \theta & \cos \theta + \color{green}{R_y}^2(1 - \cos \theta) & \color{green}{R_y}\color{blue}{R_z}(1 - \cos \theta) - \color{red}{R_x} \sin \theta & 0 \\ \color{blue}{R_z}\color{red}{R_x}(1 - \cos \theta) - \color{green}{R_y} \sin \theta & \color{blue}{R_z}\color{green}{R_y}(1 - \cos \theta) + \color{red}{R_x} \sin \theta & \cos \theta + \color{blue}{R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

Matematyczna dyskusja generowania takiej macierzy jest poza zakresem tego samouczka. Pamiętaj, że nawet ta macierz nie jest w stanie całkowicie zapobiec problemowi Gimal lock (chociaż o tą blokadę jest dużo trudniej). Aby naprawdę zapobiec problemowi Gimbal lock, musimy reprezentować obroty używając kwaternionów, które nie tylko są bezpieczniejsze, ale również bardziej przyjazne komputerom. Jednak, omównienie kwaternionów jest zarezerwowana dla późniejszego samouczka.

Łączenie macierzy

Prawdziwa moc używania macierzy transformacji polega na tym, że można łączyć wiele przekształceń w jedną, pojedynczą macierz. Przyjrzyjmy się, czy możemy wygenerować macierz transformacji, która łączy kilka przekształceń. Powiedzmy, że mamy wektor (x, y, z) i chcemy go przeskalować przez 2, a następnie przesunąć go o wektor (1,2,3). Potrzeujemy do tego macierzy translacji i macierzy skalowania. Otrzymana macierz transformacji wyglądałaby następująco:

\[Trans . Scale = \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix}\]

Zauważ, że najpierw wykonujemy translację, a następnie skalowanie podczas mnożenia macierzy. Mnożenie macierzy nie jest przemienne, co oznacza, że ich kolejność jest ważna. Podczas mnożenia macierzy, macierz po prawej stronie jest najpierw mnożona z wektorem, dlatego powinno się czytać mnożenie macierzy od prawej strony. Zaleca się najpierw wykonywanie operacji skalowania, następnie rotacji, a na końcu translacji podczas łączenia macierzy. Inaczej mogą (negatywnie) wpływać na siebie nawzajem. Na przykład, jeśli najpierw wykonasz translacje, a potem skalowanie, wektor translacji zostanie również przeskalowany!

Uruchomienie finalnej macierzy transformacji na naszym wektorze daje w wyniku wektor:

\[\begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \color{red}2x + \color{red}1 \\ \color{green}2y + \color{green}2 \\ \color{blue}2z + \color{blue}3 \\ 1 \end{bmatrix}\]

Świetnie! Wektor został najpierw przeskalowany o dwa, a następnie przesunięty o wektor (1,2,3).

Praktyka

Teraz, gdy wyjaśniliśmy całą teorię dotyczącą transformacji, nadszedł czas, aby zobaczyć, jak możemy wykorzystać tę wiedzę w praktyce. OpenGL nie ma wbudowanej klasy/struktury macierzy czy wektora, więc musimy zdefiniować własne klasy i funkcje matematyczne. W tych samouczkach wolelibyśmy uniknąć szczegółów matematycznych i po prostu skorzystać z gotowej biblioteki matematycznej. Na nasze szczęście, istnieje łatwa w obsłudze biblioteka matematyczna dla OpenGL o nazwie GLM.

GLM

Skrót GLM oznacza OpenGL Mathematics i jest biblioteką nagłówkową (ang. header-only), co oznacza, że musimy tylko dołączyć do projektu odpowiednie pliki nagłówkowe i gotowe; nie jest wymagana żadna kompilacja tej biblioteki. GLM można pobrać z tej strony internetowej (0.9.8). Następnie skopiuj katalog główny plików nagłówkowych do Twojego folderu include.

Wersja GLM 0.9.9 domyślnie inicjalizuje macierze za pomocą samych zer, zamiast tworzenia macierzy jednostkowych. Od tej wersji wymagane jest jawne inicjalizowanie typów macierzowych: glm::mat4 mat = glm::mat4(1.0f). Z powyższych powodów, dla spójności z kodem z tych samouczków zaleca się użycie wersji GLM niższej niż 0.9.9 lub zainicjalizowanie wszystkich macierzy, jak wspomniano powyżej.

Większość wymaganych funkcji GLM można znaleźć tylko w trzech plikach nagłówkowych, które dołączamy w następujący sposób:

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

Zobaczmy, czy możemy skorzystać z naszej wiedzy o transformacjach, przesuwając wektor (1,0,0) o wektor (1,1,0) (zauważ, że typujemy go jako glm::vec4 z jego współrzędną jednorodną ustawioną na 1.0):

glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);  
glm::mat4 trans;  
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));  
vec = trans * vec;  
std::cout << vec.x << vec.y << vec.z << std::endl;

Najpierw definiujemy wektor o nazwie vec, używając klasy wektora z GLM. Następnie definiujemy macierz mat4, która domyślnie jest macierzą jednostkową 4x4. Następnym krokiem jest utworzenie macierzy transformacji przez przekazanie naszej macierzy jednostkowej do funkcji glm::translate wraz z wektorem translacji (dana macierz jest następnie mnożona z macierzą translacji i zwracana jest wynikowa macierz). Potem mnożymy nasz wektor przez macierz transformacji i wypisujemy wynik. Jeśli nadal pamiętamy, jak działa translacja macierzy, to otrzymany wektor powinien być równy (1+1,0+1,0+0), co jest równe (2,1,0). Ten fragment kodu powoduje wypisanie w konsoli wartości 210, więc macierz translacji wykonała swoje zadanie.

Zróbmy coś bardziej interesującego i przeskalujmy oraz obróćmy obiekt kontenera z poprzedniego samouczka. Najpierw obracamy pojemnik o 90 stopni w kierunku przeciwnym do ruchu wskazówek zegara. Następnie skalujemy go przez wartość 0.5, co uczyni go dwukrotnie mniejszym. Utwórz najpierw macierz transformacji:

glm::mat4 trans;  
trans = glm::rotate(trans, 90.0f, glm::vec3(0.0, 0.0, 1.0));  
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5)); 

Najpierw skalujemy kontener przez wartość 0.5 na każdej osi, a następnie obracamy pojemnik o 90 stopni wokół osi Z. GLM spodziewa się kątów wyrażonch w radianach, dlatego konwertujemy stopnie na radiany za pomocą glm::radians. Zauważ, że oteksturowany prostokąt znajduje się w płaszczyźnie XY, dlatego chcemy obrócić go wokół osi Z. Ponieważ przekazujemy macierz do każdej z funkcji GLM, GLM automatycznie je mnoży, co powoduje utworzenie macierzy, która łączy wszystkie transformacje.

Następne pytanie brzmi: jak przekazać macierz transformacji do shaderów? Krótko wspomniałem wcześniej, że GLSL ma również typ mat4. Dostosujemy więc VS, aby przyjmował zmienną uniform mat4 i mnożył wektor pozycji z macierzą transformacji:

#version 330 core  
layout (location = 0) in vec3 position;  
layout (location = 1) in vec2 texCoord;

out vec2 TexCoord;

uniform mat4 transform;

void main()  
{  
  gl_Position = transform * vec4(position, 1.0f);  
  TexCoord = vec2(texCoord.x, 1.0 - texCoord.y);  
} 

GLSL posiada także typy mat2 i mat3, które umożliwiają operacje swizzlingu podobne do wektorów. Wszystkie typy operacji matematycznych (takie jak mnożenie macierzy przez skalar, mnożenie macierzy przez wektor i mnożenie macierzy przez macierz) dozwolone są dla typów macierzowych. Gdziekolwiek używane są specjalne operacje macierzowe, z pewnością wyjaśnię, co się dzieje.

Dodaliśmy zmienną uniform i pomnożyliśmy wektora położenia z macierzą transformacji, przed przekazaniem jej do zmiennej gl_Position. Nasz pojemnik powinien teraz być dwukrotnie mniejszy i obrócony o 90 stopni (przechylony w lewo). Nadal musimy przekazać macierz transformacji do shader’a:

GLuint transformLoc = glGetUniformLocation(ourShader.Program, "transform");  
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));

Najpierw pobieramy lokalizację zmiennej uniform, a następnie wysyłamy dane macierzy do shaderów za pomocą funkcji glUniform z przyrostkiem Matrix4fv. Pierwszy argument powinien być już nam doskonale znany - jest to lokalizacja uniforma. Drugi argument mówi OpenGL o liczbie macierzy, które chcemy wysłać, w naszym wypadku 1. Trzeci argument pyta nas, czy chcemy transponować naszą macierz, czyli czy zamienić kolumny z wierszami. Programiści OpenGL często używają układu macierzy, zwanego column-major ordering, który jest domyślnym układem macierzy w GLM i OpenGL, więc nie ma potrzeby transponowania macierzy; ustawiamy ten parametr na GL_FALSE. Ostatnim parametrem są rzeczywiste dane macierzy. GLM nie przechowuje macierzy w dokładnie taki sam sposób, w jaki OpenGL lubi je otrzymywać, dlatego najpierw przekształcamy wskaźnik do tych danych za pomocą wbudowanej funkcji GLM value_ptr.

Stworzyliśmy macierz transformacji, zadeklarowaliśmy zmienne uniform w shaderze wierzchołków i wysłaliśmy macierz do shaderów, gdzie przekształcamy nasze współrzędne wierzchołków. Wynik powinien wyglądać tak:

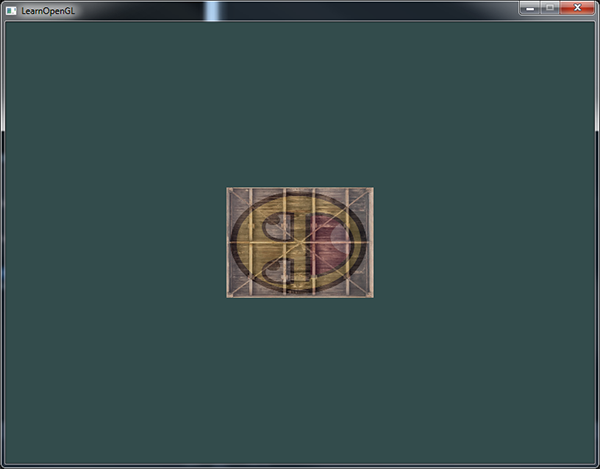
Świetnie! Nasz pojemnik jest rzeczywiście przechylony w lewo i dwa razy mniejszy, więc transformacja się powiodła. Idźmy na całość i zobaczmy, czy możemy obracać pojemnik w czasie i dla zabawy zmienimy również położenie pojemnika, tak by pokazał się w dolnej prawej części okna. Aby obracać pojemnik w czasie, musimy aktualizować macierz transformacji w głównej pętli gry, ponieważ wymaga ona aktualizacji w każdej iteracji renderowania. Używamy funkcji GLFW do pobierania czasu, aby uzyskać zmianę kąta w czasie:

glm::mat4 trans;  
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));  
trans = glm::rotate(trans,(GLfloat)glfwGetTime() * 50.0f, glm::vec3(0.0f, 0.0f, 1.0f));

Pamiętaj, że w poprzednim przypadku mogliśmy zadeklarować macierz transformacji w dowolnym miejscu, ale teraz musimy ją tworzyć przy każdej nowej iteracji, abyśmy ciągle aktualizowali rotację. Oznacza to, że musimy ponownie utworzyć macierz transformacji w każdej iteracji pętli gry. Zwykle podczas renderowania scen mamy kilka macierzy transformacji, które są odtwarzane z nowymi wartościami dla każdej nowej iteracji.

Najpierw obracamy pojemnik wokół punktu początkowego (0,0,0), a po jego obróceniu, przesuwamy jego obróconą wersję do prawego dolnego rogu ekranu. Pamiętaj, że łączenie transformacji powinno być odczytywane od tyłu: nawet jeśli w kodzie najpierw przesuwamy, a następnie obracamy obiekt, to transformacje najpierw stosują rotację, a następnie translację. Zrozumienie wszystkich tych kombinacji przekształceń i ich zastosowania do obiektów jest trudne do zrozumienia. Wypróbuj i przetestuj transformacje takie jak te, a na pewno szybko je zrozumiesz.

Jeśli zrobiłeś wszystko dobrze, powinieneś otrzymać następujący wynik:

Mamy teraz przesunięty pojemnik, który jest obracany w czasie, wszystko wykonane przez pojedynczą macierz transformacji! Teraz możesz zobaczyć, dlaczego macierze są tak potężnym narzędziem w grafice komputerowej. Możemy zdefiniować nieskończoną liczbę przekształceń i łączyć je wszystkie w jednej macierzy, którą możemy ponownie wykorzystać, tak często, jak chcemy. Korzystanie z takich transformacji w Vertex Shader pozwala nam zaoszczędzić czas na ponowne zdefiniowanie danych wierzchołkowych i zaoszczędzić czas przetwarzania, ponieważ nie musimy ponownie wysyłać naszych danych przez cały czas (co jest bardzo powolne).

Jeśli nie uzyskałeś prawidłowego wyniku lub gdzieś utknąłeś spójrz na kod źródłowy.

W następnym samouczku omówimy, jak możemy użyć macierzy do definiowania różnych układów współrzędnych dla naszych wierzchołków. To będzie nasz pierwszy krok do w stronę prawdziwej grafiki 3D w czasie rzeczywistym!

Dodatkowe materiały

• Essence of Linear Algebra: świetny viedo-tutorial Grant’a Sanderson’a o matematyce transformacji i algebrze liniowej.

Ćwiczenia

• Korzystając z ostatniej transformacji na pojemniku, spróbuj zmienić kolejność, najpierw obracając, a następnie przesuwając. Zobacz, co się dzieje i spróbuj wyjaśnić, dlaczego tak się dzieje: rozwiązanie.
• Spróbuj narysować drugi kontener z drugim wywołaniem funkcji glDrawElements, ale umieść go w innej pozycji, używając samych transformacji. Upewnij się, że ten drugi pojemnik jest umieszczony w lewym górnym rogu okna i zamiast go obracać, skaluj go w czasie (używając funkcji sin), warto zauważyć, że sin spowoduje odwrócenie obiektu po zastosowaniu ujemnej skali): rozwiązanie.