This is the Polish translation of Getting-started/Camera article of learnopengl.com tutorial series.

W poprzednim samouczku omówiliśmy macierz widoku oraz zobaczyliśmy jak możemy jej użyć do poruszania się po scenie (przesunęliśmy się trochę do tyłu). OpenGL sam w sobie nie zna koncepcji kamery, ale możemy ją symulować, przesuwając wszystkie obiekty na scenie w odwrotnym kierunku, dając iluzję, że to my się poruszamy.

W tym samouczku omówimy, jak możemy skonfigurować kamerę w OpenGL. Omówimy kamerę FPS, która pozwala swobodnie poruszać się po scenie 3D. Omówimy również obsługę klawiatury i myszy, a efektem będzie niestandardowa klasy kamery.

Przestrzeń kamery/widoku

Kiedy mówimy o przestrzeni kamery/widoku, to mówimy o wszystkich współrzędnych wierzchołków widzianych z perspektywy kamery, która jest punktem początkowym sceny: macierz widoku przekształca wszystkie współrzędne świata w współrzędne widoku, które są umieszczone względem pozycji i kierunku kamery. Aby zdefiniować kamerę, potrzebujemy jej pozycji w przestrzeni świata, kierunku, w którym patrzy, wektora wskazującego w prawo i wektora skierowanego w górę od kamery. Uważny czytelnik może zauważyć, że faktycznie będziemy tworzyć układ współrzędnych z 3 prostopadłymi do siebie osiami jednostkowymi z pozycją kamery jako początkiem układu.

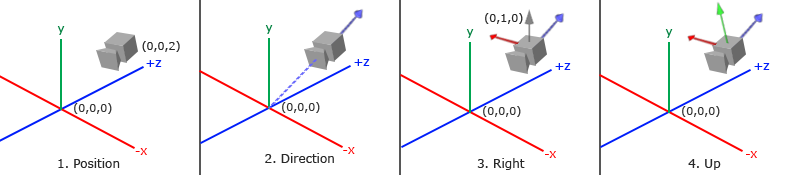
1. Pozycja kamery

Uzyskanie pozycji kamery jest łatwe. Pozycja kamery jest w zasadzie wektorem w przestrzeni świata, który wskazuje na pozycję kamery. Ustawiamy kamerę w tej samej pozycji, w jakiej ustawiliśmy ją w poprzednim tutorialu:

glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);

Nie zapominaj, że dodatnia oś z wychodzi z ekranu Twojego monitora, więc jeśli chcemy, aby kamera poruszyła się do tyłu, to przesuwamy ją wzdłuż dodatniej osi z.

2. Kierunek kamery

Kolejnym wymaganym wektorem jest kierunek kamery, t.j. w jakim kierunku patrzy. Na razie pozwalamy kamerze skierować się na punkt początkowy naszej sceny: (0,0,0). Odjęcie wektora położenia kamery od wektora początkowego sceny daje w rezultacie wektor kierunku. Ponieważ wiemy, że kamera skierowana jest w stronę kierunku ujemnej osi z, chcemy, aby wektor kierunku był skierowany ku dodatniej osi z kamery. Jeśli zmienimy kolejność odejmowania, otrzymamy wektor skierowany ku dodatniej osi z kamery:

glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);  
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);

Nazwa wektor kierunku (ang. direction vector) nie jest najlepszym wyborem, ponieważ ten wektor rzeczywiście jest skierowany w drugą stronę niż to, na co jest skierowany.

3. Prawa oś (ang. right axis)

Następnym wektorem, który potrzebujemy, jest prawy wektor, który reprezentuje dodatnią oś x, w przestrzeni kamery. Aby uzyskać prawy wektor, używamy pewnej sztuczki, najpierw określając górny wektor, który skierowany jest ku górze (w przestrzeni świata). Następnie wykonujemy iloczyn wektorowy na wektorze górnym i wektorze kierunku z kroku 2. Ponieważ wynikiem iloczynu wektorowego jest wektor prostopadły do obu wektorów, to otrzymamy wektor, który wskazuje na dodatnią oś x (jeśli zmienimy kolejność wektorów, to otrzymamy wektor, który wskazuje na ujemną oś x):

glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);  
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));

4. Górna oś (ang. Up axis)

Teraz, gdy mamy zarówno wektor osi x, jak i wektor osi z, pobranie wektora, który wskazuje na dodatnią oś y jest stosunkowo proste: wykonujemy iloczyn wektorowy wektora prawego i kierunku:

glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);

Za pomocą iloczynu wektorowego i kilku sztuczek udało się stworzyć wszystkie wektory, które tworzą przestrzeń widoku/kamery. Dla czytelników zainteresowanych matematyka, proces ten jest znany jako proces Gram-Schmidt’a w algebrze liniowej. Używając tych wektorów możemy teraz utworzyć macierz LookAt (pol. spójrz na), która okazuje się być bardzo użyteczna przy tworzeniu kamery.

LookAt

Świetną rzeczą dotyczącą macierzy jest to, że jeśli zdefiniujesz przestrzeń współrzędnych za pomocą 3 prostopadłych (lub nie liniowych) osi, możesz utworzyć macierz z tymi 3 osiami i wektorem translacji, dzięki czemu można przekształcić dowolny wektor do tego stworzonego układu współrzędnych, mnożąc ten wektor przez tą macierz. To jest dokładnie to, co robi macierz LookAt. Teraz, gdy mamy trzy prostopadłe osie i wektor położenia, możemy utworzyć własną macierz LookAt:

\[LookAt = \begin{bmatrix} \color{red}{R_x} & \color{red}{R_y} & \color{red}{R_z} & 0 \\ \color{green}{U_x} & \color{green}{U_y} & \color{green}{U_z} & 0 \\ \color{blue}{D_x} & \color{blue}{D_y} & \color{blue}{D_z} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & -\color{purple}{P_x} \\ 0 & 1 & 0 & -\color{purple}{P_y} \\ 0 & 0 & 1 & -\color{purple}{P_z} \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

Gdzie $\color{red}R$ jest prawym wektorem, $\color{green}U$ jest górnym wektorem, $\color{blue}D$ jest wektorem kierunku, a $\color{purple}P$ jest wektorem pozycji kamery. Zauważ, że wektor pozycji jest odwrócony, ponieważ ostatecznie chcemy przesunąć świat w przeciwnym kierunku, do którego chcemy się poruszać. Korzystanie z macierzy LookAt jako naszej macierzy widoku skutecznie przekształca wszystkie współrzędne świata w przestrzeń widoku, którą właśnie zdefiniowaliśmy. Macierz LookAt robi dokładnie to, co mówi: tworzy ona macierz widoku, która patrzy na dany obiekt/punkt.

Na szczęście, GLM robi to wszystko za nas. Musimy jedynie określić pozycję kamery, punkt na jaki ma być skierowana i górny wektor, który reprezentuje wektor w przestrzeni świata (górny wektor do obliczania prawego wektora). Następnie GLM tworzy macierz LookAt, którą możemy użyć jako naszą macierz widoku:

glm::mat4 view;  
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),  
glm::vec3(0.0f, 0.0f, 0.0f),  
glm::vec3(0.0f, 1.0f, 0.0f));

Funkcja glm::lookAt wymaga wektora pozycji, punktu, na którzy ma być skierowana kamera i górnego wektora. Tworzy to macierz widoku, która jest taka sama, jak ta używana w poprzednim samouczku.

Zanim wejdziemy w obsługę I/O, obróćmy kamerę wokół naszej sceny, cały czas utrzymujemy cel patrzenia na punkcie (0,0,0).

Używamy trochę trygonometrii, aby utworzyć współrzędne x i z, w każdej ramce, które reprezentują punkt na okręgu, którego użyjemy dla naszej pozycji kamery. Poprzez ponowne obliczanie współrzędnych x i z, przechodzimy przez wszystkie punkty na okręgu, a zatem kamera obraca się wokół sceny. Rozszerzymy ten okrąg o zdefiniowany promień i tworzymy nową macierz widok w każdej iteracji renderingu z użyciem funkcji GLFW glfwGetTime:

GLfloat radius = 10.0f;  
GLfloat camX = sin(glfwGetTime()) * radius;  
GLfloat camZ = cos(glfwGetTime()) * radius;  
glm::mat4 view;  
view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0));

Jeśli uruchomisz ten kod, powinieneś otrzymać coś takiego:

Dzięki temu małemu fragmentowi kodu, kamera obraca się wokół sceny w czasie. Zapraszam do eksperymentowania z parametrami promienia i pozycji/kierunku, aby zrozumieć, jak działa macierz LookAt. Sprawdź również kod źródłowy, jeśli jesteś coś Ci nie wychodzi.

Poruszanie się po scenie

Samoczynne poruszanie się kamery po scenie jest niewątpliwie świetną zabawą, ale lepszą zabawą jest kontrolowanie ruchu kamery przez nas! Najpierw musimy skonfigurować system kamery, dlatego warto jest zdefiniować niektóre zmienne kamery, na samej górze naszego programu:

glm::vec3 cameraPos   = glm::vec3(0.0f, 0.0f,  3.0f);  
glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f);  
glm::vec3 cameraUp    = glm::vec3(0.0f, 1.0f,  0.0f);

Funkcja LookAt wygląda teraz tak:

view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);

Najpierw ustawiamy pozycję kamery na uprzednio zdefiniowaną wartość zmiennej cameraPos. Kierunek to bieżąca pozycja + wektor kierunku, który wcześniej zdefiniowaliśmy. Zapewnia to, to, że kiedy poruszamy się kamerą, to będzie ona skierowana na punkt docelowy. Pobawmy się trochę tymi zmiennymi, aktualizując wektor cameraPos po naciśnięciu niektórych klawiszy.

Zdefiniowaliśmy już wcześniej funkcję processInput, aby zarządzać wszystkimi zdarzeniami pochodzącymi od klawiatury, więc dodajmy do niej kilka warunków do obsługi nowych klawiszy:

void processInput(GLFWwindow *window)  
{  
    ...  
    float cameraSpeed = 0.05f; // dopasuj do swoich potrzeb  
    if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)  
    cameraPos += cameraSpeed * cameraFront;  
    if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)  
    cameraPos -= cameraSpeed * cameraFront;  
    if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)  
    cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;  
    if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)  
    cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;  
}

Każdorazowe naciśnięcie jednego z klawiszy WASD spowoduje aktualizację pozycji kamery. Jeśli chcemy poruszać się do przodu lub do tyłu, dodajemy lub odejmujemy wektor kierunku od wektora położenia. Jeśli chcemy przesuwać się na boki, wykonujemy iloczyn wektorowy, aby utworzyć prawy wektor i odpowiednio poruszać się wzdłuż tego wektora w prawo. Powoduje to znajomy efekt, tzw. strafe, podczas używania aparatu.

Zauważmy, że normalizujemy otrzymany prawy wektor. Jeśli nie znormalizujemy tego wektora, wynikowy iloczyn wektorowy może zwracać wektory o różnej wielkości bazując na zmiennej cameraFront. Jeśli nie będziemy normalizować tego wynikowego wektora, to będziemy poruszać się albo bardzo powoli albo bardzo szybko w oparciu o orientację kamery, a nie ze stałą prędkością.

Do tej pory powinieneś już być w stanie poruszać się kamerą, choć z prędkością określoną przez aplikację, w której może być konieczne dostosowanie zmiennej cameraSpeed.

Prędkość ruchu

Obecnie używamy stałej wartości dla prędkości poruszania się po scenie. W teorii to wydaje się dobre, ale w praktyce ludzie mają różne komputery z różną mocą obliczeniową, co w wyniku daje to, że niektóre komputery są w stanie narysować znacznie więcej ramek niż inne w przeciągu sekundy. Za każdym razem, gdy jeden narysuje więcej ramek niż inny, to również częściej wywoła funkcję processInput. W rezultacie niektóre osoby mogą poruszać się naprawdę szybko, a niektóre bardzo wolno w zależności od konfiguracji sprzętu. Kiedy chcesz udostępnić swoją aplikację innym, to chcesz mieć pewność, że działa ona tak samo na wszystkich rodzajach sprzętu.

Aplikacje graficzne i gry zwykle śledzą zmienną deltaTime, która przechowuje czas, który był potrzebny do wyrenderowania ostatniej klatki. Następnie mnożymy wszystkie prędkości z wartością deltaTime. Rezultatem jest to, że gdy w ramce znajduje się duża wartość deltaTime, co oznacza, że ostatnia klatka renderowała się dłużej niż zwykle, to prędkość dla tej ramki również będzie nieco wyższa, aby wszystko zbalansować. Używając tego podejścia nie ma znaczenia, czy masz bardzo szybki czy wolny komputer, prędkość poruszania się kamery będzie odpowiednio wyważona, więc każdy użytkownik będzie miał takie samo doświadczenie.

Aby obliczyć wartość deltaTime śledzimy 2 zmienne globalne:

GLfloat deltaTime = 0.0f; // Czas pomiędzy obecną i poprzednią klatką  
GLfloat lastFrame = 0.0f; // Czas ostatniej ramki

W każdej ramce obliczamy nową wartość deltaTime w celu późniejszego wykorzystania:

GLfloat currentFrame = glfwGetTime();  
deltaTime = currentFrame - lastFrame;  
lastFrame = currentFrame; 

Teraz, gdy mamy deltaTime możemy wziąć tą wartość pod uwagę przy obliczaniu prędkości:

void do_Movement()  
{  
    GLfloat cameraSpeed = 2.5f * deltaTime;  
    ...  
}

Razem z poprzednią sekcją powinniśmy teraz mieć bardziej spójny system kamery do poruszania się po scenie:

Teraz mamy kamerę, która wygląda i porusza się tak samo szybko na każdym innym komputerze. Sprawdź kod źródłowy, jeśli masz jakieś problemy. Wartość deltaTime często będzie powracać wraz z pojawianiem się zagadnień związanych z ruchem.

Rozglądanie się

Używanie samych klawiszy do poruszania się po scenie nie jest zbyt zachwycające. Zwłaszcza, że nie możemy się odwrócić, ograniczając nasz ruch. To jest moment, w którym mysz wkracza do akcji!

Aby rozejrzeć się po scenie musimy zmieniać wektor cameraFront na podstawie danych pochodzących od myszy. Zmiana kierunku wektora na podstawie rotacji myszy jest nieco skomplikowana i wymaga pewnej trygonometrii. Jeśli nie rozumiesz trygonometrii, nie martw się. Możesz po prostu przejść do sekcji kodu i wkleić go do swojego projektu; zawsze możesz wrócić później, jeśli będziesz chciał dowiedzieć się więcej.

Kąty Eulera

Kąty Eulera to 3 wartości, które mogą reprezentować dowolny obrót 3D, określony przez Leonharda Eulera w XVIII wieku. Istnieją trzy kąty Eulera: pitch, yaw i roll. Poniższy obraz nadaje im wizualne znaczenie:

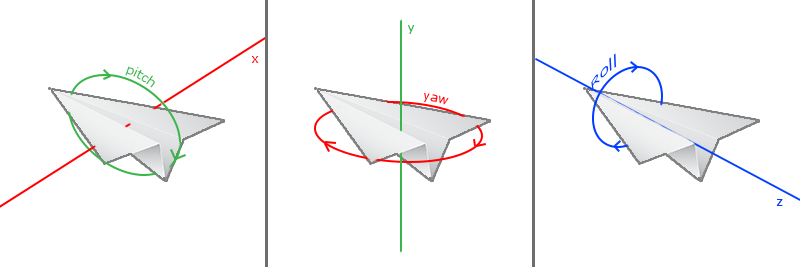
Pitch to kąt, który obrazuje, jak bardzo patrzymy w górę lub w dół, co widać na pierwszym obrazie. Drugi obraz przedstawia wartość yaw, która reprezentuje wielkość tego jak bardzo patrzymy w lewo lub w prawo. Roll oznacza, jak bardzo się turlamy, co jest najczęściej używane w statkach kosmicznych i powietrznych. Każdy z kątów Eulera jest reprezentowany przez pojedynczą wartość, a za pomocą kombinacji wszystkich trzech z nich możemy obliczyć dowolny wektor rotacji w 3D.

W naszym systemie kamery interesują nas tylko wartości pitch i yaw, więc nie omówimy tutaj wartości roll. Biorąc pod uwagę pitch i yaw możemy przekształcić je w wektor 3D reprezentujący nowy wektor kierunku. Proces przekształcania wartości pitch i yaw do wektora kierunku wymaga trochę trygonometrii. Zaczynamy od podstawowego przypadku:

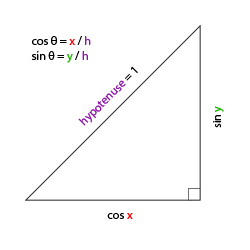
Jeśli zdefiniujmy, że przeciwprostokątna ma długość 1, to wiemy z trygonometrii, że długość jednej przyprostokątnej wynosi $\cos \ \color{red}x/\color{purple}h = \cos \ \color{red}x/\color{purple}1 = \cos\ \color{red}x$, a drugiej wynosi $\sin \ \color{green}y/\color{purple}h = \sin \ \color{green}y/\color{purple}1 = \sin\ \color{green}y$. Daje to nam pewne ogólne wzory do pobierania długości w obu kierunkach x i y, w zależności od podanego kąta. Użyjmy tego do obliczenia elementów wektora kierunku:

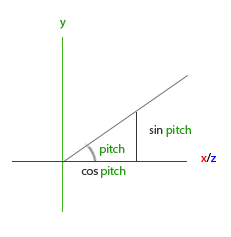
Ten trójkąt wygląda podobnie do poprzedniego trójkąta, więc jeśli wyobrazimy sobie, że siedzimy na płaszczyźnie xz i patrzmy w stronę osi y, to możemy obliczyć długość/siłę kierunku y (jak bardzo patrzymy w górę lub w dół) w oparciu o pierwszy trójkąt. Z obrazu widzimy, że wynikowa wartość y dla danej wartości pitch wynosi $\sin\ \theta$:

direction.y = sin(glm::radians(pitch)); // Zauważ, że najpierw konwertujemy kąt na radiany 

Tutaj aktualizujemy tylko wartość y, ale jeśli przyjrzysz się uważnie, możesz zauważyć, że ma to również wpływ na komponenty x i z. Z trójkąta widać, że ich wartości są równe:

direction.x = cos(glm::radians(pitch));  
direction.z = cos(glm::radians(pitch));

Zobaczmy, czy możemy znaleźć potrzebne składniki wartości yaw:

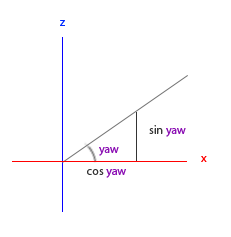
Podobnie jak trójkąt pitch, widzimy, że składnik x zależy od wartości cos(yaw), a wartość z zależy również od sinusa wartości yaw. Dodanie tego do poprzednich wartości powoduje końcowy wektor kierunku oparty na wartościach pitch i yaw:

direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw));  
direction.y = sin(glm::radians(pitch));  
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));

Daje nam to formułę do przekształcania wartości pitch i yaw do trójwymiarowego wektora kierunku, który można wykorzystać do rozglądania się. Pewnie zastanawiasz się teraz: jak mamy pobierać te wartości yaw i pitch?

Obsługa myszy

Wartości yaw i pitch są pobierane z ruchu myszy (lub kontrolera/joysticka), w którym poziomy ruch myszy wpływa na yaw, a pionowy ruch myszy wpływa na pitch. Ideą jest to, by zapisać pozycję myszy w ostatniej ramce, a w bieżącej ramce obliczyć, jak bardzo pozycja myszy uległy zmianie w porównaniu z ostatnią wartością w poprzedniej ramce. Im wyższa jest różnica w poziomie/pionie, tym bardziej aktualizujemy wartość pitch lub yaw, a tym samym aktualizujemy kierunek kamery.

Najpierw powiedzmy GLFW, że powinien ukryć kursor i jednocześnie przechwytywać go. Przechwytywanie kursora oznacza, że po aktywacji okna (ang. focus) aplikacji kursor pozostaje w oknie tej aplikacji (chyba że aplikacja traci focus lub kończy pracę). Możemy to zrobić jednym prostym wywołaniem funkcji:

glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED); 

Po tym wywołaniu, gdziekolwiek ruszymy mysz, nie będzie ona widoczna i nie powinna wychodzić z okna. Jest to idealne rozwiązanie dla systemu FPS.

Aby obliczyć wartości pitch i yaw, musimy poinformować GLFW, aby nasłuchiwał zdarzenia związanego z ruchem myszy. Wykonujemy to (podobnie do obsługi klawiatury), tworząc funkcję wywołania zwrotnego z następującym prototypem:

void mouse_callback(GLFWwindow* window, double xpos, double ypos);

Tutaj xpos i ypos reprezentują bieżące pozycje myszy. Gdy tylko zarejestrujemy funkcję wywołania zwrotnego, to za każdym razem, gdy mysz się przemieści, funkcja mouse_callback zostanie wywołana:

glfwSetCursorPosCallback(window, mouse_callback);

Podczas obsługi myszy dla kamery w stylu FPS wykonujemy kilka czynności, które musimy wykonać przed ostatecznym pobraniem wektora kierunku:

1. Obliczyć przesunięcie myszy od czasu ostatniej ramki.
2. Dodać wartość przesunięcia do wartości pitch i yaw kamery.
3. Dodać pewne ograniczenia do maksymalnych/minimalnych wartości yaw/pitch.
4. Obliczyć wektor kierunku.

Pierwszym krokiem jest obliczenie przesunięcia myszy od czasu ostatniej ramki. Najpierw musimy zapisać ostatnią pozycję myszy w aplikacji, które ustawiamy początkowo na środek ekranu (rozmiar ekranu wynosi 800 na 600):

GLfloat lastX = 400, lastY = 300;

Następnie w funkcji wywołania zwrotnego myszy obliczamy przesunięcie ruchu myszy pomiędzy ostatnią i aktualną ramką:

GLfloat xoffset = xpos - lastX;  
GLfloat yoffset = lastY - ypos; // Odwrócone, ponieważ współrzędne y zmieniają się od dołu do góry  
lastX = xpos;  
lastY = ypos;

GLfloat sensitivity = 0.05f;  
xoffset *= sensitivity;  
yoffset *= sensitivity;

Zauważmy, że mnożymy wartości przesunięcia przez wartość sensitivity. Jeśli pominiemy to mnożenie, ruch myszy byłby zbyt silny; dopasuj tę wartość do swojego gustu.

Następnie dodajemy wartość przesunięcia do globalnie zadeklarowanych wartości pitch i yaw:

yaw   += xoffset;  
pitch += yoffset; 

W trzecim kroku chcielibyśmy dodać pewne ograniczenia do obracania kamerą, aby użytkownicy nie byli w stanie robić dziwnych ruchów kamerą (zapobiega też kilku dziwacznym problemom). Pitch zostanie ograniczony w taki sposób, że użytkownicy nie będą mogli patrzeć wyżej niż 89 stopni w górę (przy 90 stopniach kamera ma skłonność do odwracania się, więc trzymamy się wartości 89 jako naszego limitu), a także nie niżej niż -89 stopni. Dzięki temu użytkownik będzie mógł spojrzeć w niebo i na nogi, ale nie wyżej/niżej. Ograniczenie działa po prostu w taki sposób, że zastępuje wartość wynikową jego wartością limitu, gdy to ograniczenie zostanie naruszone:

if(pitch > 89.0f)  
    pitch = 89.0f;  
if(pitch < -89.0f)  
    pitch = -89.0f;

Zauważmy, że nie ustawiamy ograniczenia na wartość yaw, ponieważ nie chcemy ograniczać użytkownika w ruchu poziomym. Jednakże, tak samo łatwo możesz dodać ograniczenie do wartości yaw, jeśli masz na to ochotę.

Czwarty i ostatni krok to obliczenie rzeczywistego kierunku wektora z wynikających wartości yaw i pitch, jak omówiono to w poprzedniej sekcji:

glm::vec3 front;  
front.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw));  
front.y = sin(glm::radians(pitch));  
front.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));  
cameraFront = glm::normalize(front);

Ten obliczony wektor kierunku zawiera wszystkie obroty obliczane z ruchu myszy. Ponieważ wektor cameraFront jest zawarty w funkcji glm lookAt jesteśmy gotowi, aby spiąć to wszystko razem.

Jeśli teraz uruchomisz kod, zauważysz, że kamera wykonuje nagle duży skok, gdy okno uzyska focus Twojego kursora. Przyczyną nagłego skoku jest to, że gdy tylko kursor wejdzie do okna, funkcja wywołania zwrotnego myszy jest wywoływana z położeniem xpos i ypos, równym punktowi, w którym mysz została wprowadzona w obszar okna aplikacji. Zwykle jest to pozycja, która jest dosyć daleko od środka ekranu, powodując duże przesunięcia, a więc duży skok. Możemy ominąć ten problem po prostu definiując globalną zmienną bool, aby sprawdzić, czy jest to pierwszy raz, kiedy otrzymujemy dane z myszy, jeśli tak, najpierw aktualizujemy początkowe pozycje myszy do nowego xpos i ypos; powstałe ruchy myszy będą następnie wykorzystywać wprowadzone współrzędne położenia myszy w celu obliczenia przesunięć:

if(firstMouse) // ta zmienna bool jest początkowo ustawiona na true  
{  
    lastX = xpos;  
    lastY = ypos;  
    firstMouse = false;  
}

Końcowy kod wygląda wtedy tak:

void mouse_callback(GLFWwindow* window, double xpos, double ypos)  
{  
    if(firstMouse)  
    {  
        lastX = xpos;  
        lastY = ypos;  
        firstMouse = false;  
    }

    GLfloat xoffset = xpos - lastX;  
    GLfloat yoffset = lastY - ypos;  
    lastX = xpos;  
    lastY = ypos;

    GLfloat sensitivity = 0.05;  
    xoffset *= sensitivity;  
    yoffset *= sensitivity;

    yaw += xoffset;  
    pitch += yoffset;

    if(pitch > 89.0f)  
        pitch = 89.0f;  
    if(pitch < -89.0f)  
        pitch = -89.0f;

    glm::vec3 front;  
    front.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));  
    front.y = sin(glm::radians(pitch));  
    front.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));  
    cameraFront = glm::normalize(front);  
} 

Mamy to! Wypróbuj teraz kamerę, a zobaczysz, że możesz swobodnie poruszać się po scenie 3D!

Zoom

Jako dodatek do systemu kamery dodamy również obsługę zoom’owania. W poprzednim samouczku powiedzieliśmy, że pole widzenia (ang. field of view) lub fov określa, ile możemy zobaczyć na scenie. Kiedy pole widzenia zmniejszy się, przestrzeń projekcji sceny staje się mniejsza, co daje iluzję powiększania. Aby zoomować, użyjemy kółka myszy. Podobnie jak w przypadku ruchu myszki i obsługi klawiatury, zdefiniujemy funkcję wywołania zwrotnego dla przewijania myszą:

void scroll_callback(GLFWwindow* window, double xoffset, double yoffset)  
{  
    if(fov >= 1.0f && fov <= 45.0f)  
        fov -= yoffset;  
    if(fov <= 1.0f)  
        fov = 1.0f;  
    if(fov >= 45.0f)  
        fov = 45.0f;  
}

Podczas przewijania wartość yoffset reprezentuje wartość przewijania w pionie. Kiedy wywoływana jest funkcja scroll_callback, zmieniamy wartość globalnie zadeklarowanej zmiennej fov. Ponieważ 45.0f jest domyślną wartością fov, to chcemy ograniczyć poziom zommowania pomiędzy 1.0f a 45.0f.

Teraz musimy zaktualizować macierz projekcji perspektywicznej i przesłać ją do GPU iteracji renderowania, ale tym razem ze zmienną fov:

projection = glm::perspective(glm::radians(fov), 800.0f / 600.0f, 0.1f, 100.0f);

I wreszcie nie zapomnij zarejestrować funkcji wywołania zwrotnego dla przewijania myszą:

glfwSetScrollCallback(window, scroll_callback); 

Mamy to. Zaimplementowaliśmy prosty system kamery pozwalający na swobodny ruch w środowisku 3D.

Możesz trochę poeksperymentować, a jeśli gdzieś utknąłeś, porównaj kod z kodem źródłowym.

Zauważ, że system kamery zaimplementowany za pomocą kątów Eulera nadal nie jest idealnym systemem. W zależności od ograniczeń i konfiguracji możesz jeszcze spotkać się z problemem Gimbal lock. Najlepszy system kamer mógłby być zaimplementowany przy użyciu kwaternionów, ale to zostawimy na później.

Klasa Camera

W kolejnych tutorialach zawsze będziemy korzystać z kamery, aby łatwo móc rozglądać się po scenach i zobaczyć wyniki pod różnymi kątami. Jednakże, ponieważ kamera może zajmować trochę miejsca w każdym samouczku, stworzymy własną klasę Camera, który zrobi większość za nas za pomocą kilku drobnych dodatków. W przeciwieństwie do samouczka Programów cieniujących nie będę Cię prowadził przez stworzenie klasy kamery, ale po prostu dostarczę Ci kod źródłowy (w pełni skomentowany), jeśli chciałbyś poznać to co dzieje się w środku.

Podobnie jak klasa Shader, stworzymy tą klasę całkowicie w jednym pliku nagłówkowym. Obiekt kamery można znaleźć tutaj. Teraz powinieneś być w stanie zrozumieć cały kod. Zaleca się co najmniej sprawdzenie klasy raz, aby zobaczyć, jak można utworzyć taki obiekt kamery.

Przedstawiony przez nas system kamery jest kamerą typu FPS, który odpowiada większości celów i działa dobrze z kątami Eulera, ale należy zachować ostrożność podczas tworzenia innych systemów kamer, takich jak kamera do symulacji lotniczych. Każdy system kamer ma własne sztuczki i dziwactwa, więc zapoznaj się z nimi. Na przykład ta kamera FPS nie zezwala na wartości pitch większe niż 90, a statyczny górny wektor (0,1,0) nie działa, gdy byśmy chcieli uwzględnić wartość roll.

Zaktualizowana wersja kodu źródłowego tego tutorialu, przy użyciu nowego obiektu kamery można znaleźć tutaj.

Ćwiczenia

• Zobacz, czy możesz przekształcić klasę kamery w taki sposób, że stanie się prawdziwą kamerą fps, gdzie nie można latać; można tylko rozglądać się podczas pobytu na płaszczyźnie xz: rozwiązanie.
• Spróbuj utworzyć własną funkcję LookAt, gdzie ręcznie utworzysz macierz widoku, jak omówiono to na początku tego samouczka. Zamień funkcję LookAt glm na własną implementację i sprawdź, czy nadal działa tak samo: rozwiązanie.