This is the Polish translation of Lighting/Basic-Lighting article of learnopengl.com tutorial series.
Oświetlenie w świecie rzeczywistym jest niezwykle skomplikowane i zależy od bardzo wielu czynników, na które nie możemy sobie pozwolić, ze względu na ograniczoną moc obliczeniową jaką dysponują dzisiejsze komputery. Oświetlenie w OpenGL opiera się zatem na przybliżeniach rzeczywistości przy użyciu uproszczonych modeli, które są znacznie łatwiejsze do przetworzenia i wyglądają podobnie. Te modele oświetlenia są oparte na fizyce światła, tak jak ją rozumiemy. Jeden z tych modeli nazywa się modelem oświetlenia Phong’a. Główne elementy konstrukcyjne modelu Phong’a składają się z 3 elementów: oświetlenia otoczenia (ang. ambient lighting), rozproszonego (ang. diffuse lighting) i zwierciadlanego (ang. specular lighting). Poniżej możesz zobaczyć, jak wyglądają te elementy oświetlenia:

- Oświetlenie otoczenia: nawet gdy jest ciemno, zwykle gdzieś na świecie jest jeszcze jakieś światło (księżyc, odległe światło), więc obiekty prawie nigdy nie są całkowicie ciemne. Aby to zasymulować, używamy stałej oświetlenia otoczenia, która zawsze nadaje obiektowi pewien kolor.
- Oświetlenie rozproszone: naśladuje oddziaływanie kierunkowe światła na obiekt. Jest to najbardziej wizualnie istotny element modelu oświetlenia. Im bardziej część obiektu jest skierowana w stronę źródła światła, tym jaśniejsza się staje.
- Oświetlenie zwierciadlane: symuluje jasne miejsce światła, które pojawia się na błyszczących obiektach. Te miejsca (ang. specular highlights) są często bardziej podatne na kolor światła niż kolor obiektu.
Aby stworzyć interesujące wizualnie sceny, musimy przynajmniej symulować te 3 komponenty oświetleniowe. Zaczniemy od najprostszego: oświetlenie otoczenia.
Oświetlenie otoczenia
Światło zazwyczaj nie pochodzi z jednego źródła światła, ale z wielu źródeł światła rozproszonych dookoła nas, nawet gdy nie są one od razu widoczne. Jedną z właściwości światła jest to, że może on rozproszyć się i odbić w wielu kierunkach, docierając do miejsc, które nie znajdują się w jego bezpośrednim sąsiedztwie; światło może zatem odbijać się od innych powierzchni i pośrednio wpływać na oświetlenie obiektu. Algorytmy, które biorą to pod uwagę, są nazywane algorytmami globalnej iluminacji (ang. global illumination), ale są one kosztowne obliczeniowo i/lub skomplikowane.
Ponieważ nie jesteśmy wielkimi fanami skomplikowanych i kosztownych algorytmów, zaczniemy od bardzo uproszczonego modelu globalnego oświetlenia, a mianowicie oświetlenie otoczenia. Jak widzieliśmy w poprzedniej sekcji, używamy stałego koloru (światła), który dodajemy do ostatecznego koloru fragmentów obiektu, dzięki czemu wygląda tak, jakby zawsze było jakieś rozproszone światło, nawet gdy bezpośrednie źródło światła nie pada na ten obiekt.
Dodawanie oświetlenia otoczenia do sceny jest naprawdę łatwe. Przyjmujemy kolor światła, mnożymy go przez mały, stały czynnik oświetlenia otoczenia i mnożymy go z kolorem obiektu i używamy go jako koloru fragmentu:
void main()
{
float ambientStrength = 0.1;
vec3 ambient = ambientStrength * lightColor;
vec3 result = ambient * objectColor;
FragColor = vec4(result, 1.0);
}
Jeśli teraz uruchomisz program, zauważysz, że pierwszy etap oświetlenia został pomyślnie zastosowany do twojego obiektu. Obiekt jest dość ciemny, ale nie całkowicie, ponieważ zastosowano oświetlenie otoczenia (należy zwrócić uwagę, że obiekt światła pozostaje nienaruszony, ponieważ używamy innego shader’a). Powinno to wyglądać mniej więcej tak:
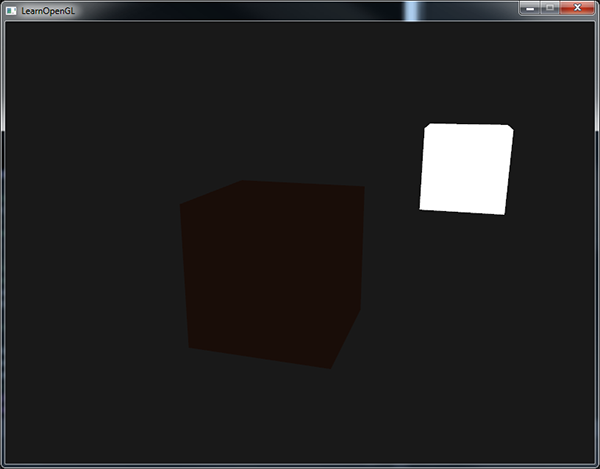
Oświetlenie rozproszone
Samo oświetlenie otoczenia nie daje najciekawszych rezultatów, ale oświetlenie rozproszone zacznie dawać znaczący wizualny efekt na obiekt. Rozproszone światło nadaje obiektowi większą jasność, im bliżej jego fragmenty są ustawione do promieni światła. Aby lepiej zrozumieć oświetlenie rozproszone, spójrz na następujący obraz:
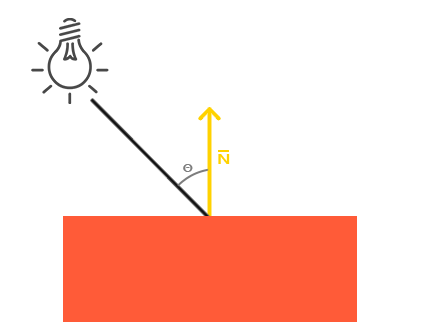
Po lewej stronie znajduje się źródło światła z promieniem światła skierowanym w stronę pojedynczego fragmentu naszego obiektu. Następnie musimy zmierzyć, pod jakim kątem promień światła “dotyka” fragmentu. Jeśli promień światła jest prostopadły do powierzchni obiektu, światło ma największy wpływ na ten fragment. Aby zmierzyć kąt pomiędzy promieniem światła i fragmentem, używamy czegoś takiego jak wektor normalny, który jest wektorem prostopadłym do powierzchni fragmentu (tutaj przedstawionym jako żółta strzałka); dojdziemy do tego później. Kąt pomiędzy dwoma wektorami można następnie łatwo obliczyć za pomocą iloczynu skalarnego (ang. dot product).
Możesz pamiętać z tutoriala o transformacjach, że im mniejszy jest kąt między dwoma wektorami jednostkowymi, tym bardziej iloczyn skalarny jest nachylony w kierunku wartości 1. Gdy kąt między dwoma wektorami wynosi 90 stopni, iloczyn skalarny przyjmuje wartość 0. To samo dotyczy $\theta$: im większy kąt $\theta$, tym mniejszy wpływ światła na kolor fragmentu.
Zauważ, że aby uzyskać (tylko) cosinus kąta między obydwoma wektorami, najlepiej jest pracować z wektorami jednostkowymi (ang. unit vectors) - wektorami o długości 1. Więc musimy upewnić się, że wszystkie wektory są znormalizowane, w przeciwnym razie iloczyn skalarny zwróci więcej niż tylko cosinus (patrz Transformacje).
Otrzymana wartość iloczynu skalarnego zwraca jest skalarem, który możemy wykorzystać do obliczenia wpływu światła na kolor fragmentu, w wyniku czego powstają odmiennie oświetlone fragmenty, w oparciu o ich orientację względem kierunku światła.
A więc, czego potrzebujemy do obliczenia oświetlenia rozproszonego?
- Wektor normalny: wektor prostopadły do powierzchni wierzchołka.
- Promień światła: wektor kierunkowy, który jest wektorem różnicy między położeniem światła, a położeniem fragmentu. Aby obliczyć promień światła, potrzebujemy wektora pozycji światła i wektora położenia fragmentu.
Wektory normalne
Wektor normalny to wektor (jednostkowy), który jest prostopadły do powierzchni wierzchołka. Ponieważ wierzchołek nie ma powierzchni (to tylko pojedynczy punkt w przestrzeni), obliczamy wektor normalny wykorzystując otaczające go wierzchołki, aby obliczyć powierzchnię wierzchołka. Możemy użyć małej sztuczki, aby obliczyć wektory normalne dla wszystkich wierzchołków sześcianu przy pomocy iloczynu wektorowego. Ponieważ kostka 3D nie jest skomplikowanym kształtem, możemy po prostu ręcznie dodać je do danych wierzchołków. Zaktualizowaną tablicę danych wierzchołków można znaleźć tutaj. Spróbujcie wyobrazić sobie, że wektory normalne są w istocie wektorami prostopadłymi do płaszczyzn powierzchni sześcianu (sześcian składa się z 6 płaszczyzn).
Ponieważ dodaliśmy dodatkowe dane do tablicy wierzchołków, powinniśmy zaktualizować Vertex Shader oświetlenia:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
...
Skoro dodaliśmy wektor normalny do każdego z wierzchołków i zaktualizowaliśmy Vertex Shader, to także powinniśmy zaktualizować atrybutów wierzchołków. Zwróć uwagę, że obiekt lampy używa tej samej tablicy wierzchołków dla swoich danych wierzchołków, ale Vertex Shader lampy nie ma zastosowania do nowo dodanych wektorów normalnych. Nie musimy aktualizować shader’ów lampy ani konfiguracji atrybutów, ale musimy przynajmniej zmodyfikować wskaźniki atrybutów wierzchołków, aby odzwierciedlić nowy rozmiar tablicy wierzchołków:
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);
Chcemy użyć tylko pierwszych 3 float’ów każdego wierzchołka i zignorować ostatnie 3 float’y, więc musimy zaktualizować tylko parametr stride do 6-krotności rozmiaru typu float i gotowe.
Może to wyglądać nieefektywnie, że używamy danych wierzchołków, które nie są w pełni wykorzystywane przez shader lampy, ale dane wierzchołków są już przechowywane w pamięci GPU, które pochodzą z obiektu kontenera, więc nie musimy przechowywać nowych danych w pamięci GPU. Dzięki temu jest on bardziej wydajny w porównaniu z przydzieleniem nowego VBO specjalnie dla lampy.
Wszystkie obliczenia oświetlenia są wykonywane w Fragment Shader, więc musimy przesłać wektory normalne z Vertex Shader’a do Fragment Shader’a. Zróbmy to:
out vec3 Normal;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
Normal = aNormal;
}
Pozostaje tylko zadeklarować odpowiednią zmienną wejściową w Fragment Shader:
in vec3 Normal;
Obliczanie koloru rozproszonego
Mamy teraz wektor normalny dla każdego wierzchołka, ale wciąż potrzebujemy wektora położenia światła i wektora położenia fragmentu. Ponieważ pozycja światła jest tylko pojedynczą zmienną statyczną, możemy po prostu zadeklarować ją jako uniform w Fragment Shader:
uniform vec3 lightPos;
A następnie zaktualizujmy uniform w pętli gry (lub na zewnątrz, ponieważ się nie zmienia). Używamy wektora lightPos zadeklarowanego w poprzednim samouczku jako lokalizacji źródła światła:
lightingShader.setVec3("lightPos", lightPos);
Ostatnią rzeczą, jakiej potrzebujemy, jest faktyczna pozycja fragmentu. Wykonamy wszystkie obliczenia oświetlenia w przestrzeni świata, więc chcemy pozycji wierzchołka, która znajduje się w przestrzeni świata. Możemy to osiągnąć, mnożąc atrybut pozycji wierzchołka tylko z macierzą modelu (nie macierzą widoku i macierzy projekcji), aby przekształcić ją we współrzędne przestrzeni świata. Można to łatwo osiągnąć w Vertex Shader, więc zadeklaruj zmienną wyjściową i oblicz jej współrzędne w przestrzeni świata:
out vec3 FragPos;
out vec3 Normal;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
FragPos = vec3(model * vec4(aPos, 1.0));
Normal = aNormal;
}
Na koniec dodaj odpowiednią zmienną wejściową do Fragment Shader’a:
in vec3 FragPos;
Po ustawieniu wszystkich wymaganych zmiennych możemy zacząć od obliczenia oświetlenia w Fragment Shader.
Pierwszą rzeczą, którą musimy obliczyć, jest wektor kierunkowy między źródłem światła a pozycją fragmentu. Wspomnieliśmy, że wektor kierunkowy światła jest wektorem różnicy między wektorem pozycji światła a wektorem pozycji fragmentu. Jak możesz sobie przypomnieć z samouczka o transformacjach, możemy łatwo obliczyć tę różnicę, odejmując oba wektory. Chcemy również upewnić się, że wszystkie odpowiednie wektory będą wektorami jednostkowymi, więc normalizujemy zarówno wektor normalny, jak i wynikowy wektor kierunku:
vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos);
Przy obliczaniu oświetlenia zwykle nie dbamy o wielkość wektora lub jego położenie; dbamy tylko o ich kierunek. Ponieważ zależy nam tylko na ich kierunku, prawie wszystkie obliczenia są wykonywane za pomocą wektorów jednostkowych, ponieważ upraszcza to większość obliczeń (jak iloczyn skalarny). Więc podczas wykonywania obliczeń oświetlenia, upewnij się, że zawsze normalizujesz odpowiednie wektory. Zapomnienie o normalizacji wektora jest popularnym błędem.
Następnie chcemy obliczyć rzeczywisty rozproszony wpływ światła na bieżący fragment, obliczając iloczyn skalarny pomiędzy wektorami norm i lightDir. Otrzymana wartość jest następnie mnożona przez kolor światła, aby uzyskać komponent rozproszony, co powoduje ciemniejszą składową rozproszoną, im większy kąt znajduje się pomiędzy dwoma wektorami:
float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;
Jeśli kąt między obydwoma wektorami jest większy niż 90 stopni, wynik iloczynu skalarnego faktycznie stanie się ujemny i otrzymamy ujemny komponent rozproszony. Z tego powodu używamy funkcji max, która zwraca wyższą wartość z dwóch wartości, aby upewnić się, że komponent rozproszony (a więc i kolory) nigdy nie będzie ujemny. Oświetlenie dla negatywnych wartości kolorów nie jest tak naprawdę zdefiniowane, więc najlepiej jest trzymać się z daleka od tego, chyba że jesteś jednym z tych ekscentrycznych artystów.
Teraz, gdy mamy zarówno komponent oświetlenia otoczenia, jak i rozproszony, dodajemy do siebie oba kolory, a następnie mnożymy wynik przez kolor obiektu, aby otrzymać wyjściowy kolor fragmentu:
vec3 result = (ambient + diffuse) * objectColor;
FragColor = vec4(result, 1.0);
Jeśli twoja aplikacja (i shadery) zostały skompilowane pomyślnie, powinieneś zobaczyć coś takiego:
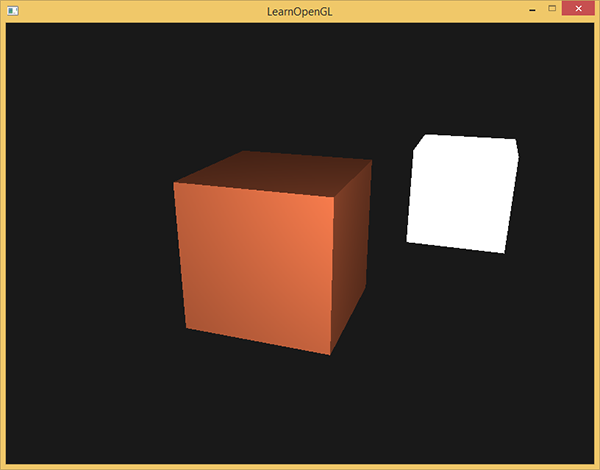
Widać, że przy rozproszonym oświetleniu sześcian zaczyna wyglądać jak rzeczywisty sześcian. Spróbuj zwizualizować normalne wektory w swojej głowie i poobracaj kostką, aby zobaczyć, że im większy kąt między nimi a kierunkiem światła, tym ciemniejszy staje się fragment.
Jeśli utkniesz, możesz porównać swój kod źródłowy z pełnym kodem źródłowym tutaj.
Ostatnia rzecz
Do tej chwili przekazywaliśmy wektory normalne bezpośrednio z Vertex Shader’a do Fragment Shader’a. Jednak obliczenia, które wykonywaliśmy w Fragment Shader, są wykonywane we współrzędnych przestrzeni światowej, więc czy nie powinniśmy również przekształcać wektorów normalnych do współrzędnych w przestrzeni świata? Zasadniczo tak, ale nie jest to tak proste, jak proste pomnożenie go przez macierz modelu.
Po pierwsze, wektory normalne są tylko wektorami kierunkowymi i nie reprezentują określonej pozycji w przestrzeni. Ponadto, wektory normalne nie mają homogenicznej współrzędnej (składnik w pozycji wierzchołka). Oznacza to, że translacje nie mają żadnego wpływu na wektory normalne. Jeśli więc chcemy pomnożyć wektory normalne przez macierz modelu, to chcemy usunąć część translacyjną macierzy, biorąc lewą górną macierz 3x3 modelu (zauważmy, że możemy również ustawić składową w wektora normalnego na 0 i pomnożyć go przez macierz 4x4, co również spowoduje usunięcie translacji). Jedyne transformacje, które chcemy zastosować do wektorów normalnych, to transformacje skali i rotacji.
Po drugie, jeśli macierz modelu wykonywałaby nierównomierną skalę, wierzchołki zmieniałyby się w taki sposób, że wektor normalny nie byłby już prostopadły do powierzchni, więc nie możemy przekształcić wektorów normalnych za pomocą takiej macierzy modelu. Poniższy obrazek pokazuje wpływ takiej macierzy modelu (z nierównomiernym skalowaniem) na wektor normalny:
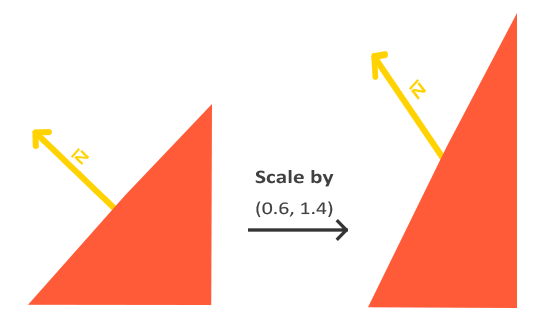
Za każdym razem, gdy stosujemy nierównomierną skalę (uwaga: jednolita skala nie zaszkodzi normalnym, ponieważ ich kierunki się nie zmieniają, tylko ich wielkość, która jest łatwa do ustalenia przez normalizację), wektory normalne nie są już prostopadłe do odpowiedniej powierzchni, co zniekształca oświetlenie.
Sztuczka polegająca na naprawie tego zachowania polega na użyciu innej macierzy modelu specjalnie dostosowanej do wektorów normalnych. Ta macierz nazywa się macierzą normalnych (ang. normal matrix) i wykorzystuje kilka liniowych operacji algebraicznych, aby usunąć efekt nieprawidłowego skalowania wektorów normalnych. Jeśli chcesz wiedzieć, w jaki sposób ta macierz jest obliczana, proponuję następujący artykuł (wersja ang.).
Macierz normalnych jest zdefiniowana jako “transpozycja odwrotności lewego górnego rogu macierzy modelu”. Uff, jeśli do końca nie rozumiesz, co to oznacza, nie martw się; nie omówiliśmy jeszcze macierzy odwrotnej i transpozycyjnej. Zwróć uwagę, że większość zasobów definiuje macierz normalną, ponieważ te operacje są stosowane do macierzy modelu-widoku, ale ponieważ pracujemy w przestrzeni świata (a nie w przestrzeni widoku), używamy tylko macierzy modelu.
W Vertex Shader możemy sami wygenerować tę macierz normalną, używając funkcji inverse i transpose, które działają na dowolnym typie macierzowym. Zauważ, że również rzutujemy macierz na macierz 3x3, aby upewnić się, że traci ona swoje właściwości translacyjne i że może ona być mnożona z wektorem normalnym vec3:
Normal = mat3(transpose(inverse(model))) * aNormal;
W sekcji oświetlenia rozproszonego, oświetlenie było w porządku, ponieważ nie wykonaliśmy żadnej operacji skalowania na samym obiekcie, więc nie było potrzeby korzystania z macierzy normalnych i mogliśmy po prostu pomnożyć wartości wektorów normalnych z macierzą modelu. Jeśli jednak wykonujesz nierównomierną skalę, ważne jest, aby pomnożyć wektor normalny z macierzą normalnych.
Inwersja (odwrotność) macierzy jest kosztowną operacją nawet dla shaderów, więc w miarę możliwości staraj się unikać tej operacji w shader’ach, ponieważ są one wykonywane dla każdego wierzchołka/fragmentu sceny. Dla celów edukacyjnych jest to w porządku, ale dla wydajnej aplikacji prawdopodobnie będziesz chciał obliczyć macierz normalnych na procesorze i przesłać ją do shader’ów za pomocą uniforma przed rysowaniem (podobnie jak macierz modelu).
Oświetlenie zwierciadlane
Jeśli nie jesteś jeszcze wyczerpany wszystkimi obliczeniami oświetlenia, możemy pomału kończyć omawianie modelu Phonga. Zostały nam tylko zwierciadlane refleksy.
Podobnie jak oświetlenie rozproszone, oświetlenie zwierciadlane jest oparte na wektorze kierunku światła i wektorach normalnych obiektu, ale tym razem jest również oparte na kierunku widzenia, np. z którego kierunku gracz patrzy na fragment. Oświetlenie zwierciadlane opiera się na właściwościach odblaskowych światła. Jeśli myślimy o powierzchni obiektu jako lustrze, to oświetlenie zwierciadlane jest najsilniejsze, gdy widzimy światło odbite na powierzchni. Efekt ten można zobaczyć na następującym obrazie:
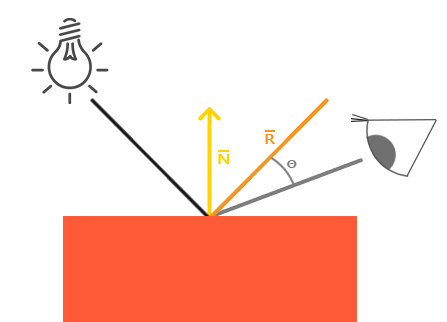
Obliczamy wektor odbicia, odbijając kierunek światła względem wektora normalnego. Następnie obliczamy odległość kątową między tym wektorem odbicia a kierunkiem widoku i im mniejszy jest kąt między nimi, tym większy jest wpływ światła zwierciadlanego. Wynikający z tego efekt jest taki, że widzimy refleks, gdy patrzymy zgodnie z kierunkiem światła odbitym przez obiekt.
Wektor widzenia to dodatkowa zmienna, której potrzebujemy do oświetlenia zwierciadlanego, którą możemy obliczyć za pomocą pozycji widza w przestrzeni świata i położenia fragmentu. Następnie obliczamy intensywność oświetlenia zwierciadlanego. Następnie pomnóżmy to przez kolor światła i dodajmy do wcześniej obliczonych komponentów światła otoczenia i rozproszonego.
Wybraliśmy obliczenia oświetlenia w przestrzeni świata, ale większość ludzi woli robić oświetlenie w przestrzeni widoku/kamery. Dodatkową zaletą obliczania w przestrzeni widoku jest to, że pozycja widza jest zawsze ustawiona na (0,0,0), więc dostajesz pozycję kamery za darmo. Uważam jednak, że obliczanie oświetlenia w przestrzeni świata jest bardziej intuicyjne w celach edukacyjnych. Jeśli nadal chcesz obliczyć oświetlenie w przestrzeni widoku, to musisz przekształcić wszystkie odpowiednie wektory za pomocą macierzy widoku (nie zapomnij również zmienić macierzy normalnych).
Aby uzyskać pozycję widza w przestrzeni świata, po prostu bierzemy wektor pozycji obiektu kamery (który jest oczywiście widzem). Dodajmy więc kolejny uniform do Fragment Shader i przekażmy odpowiedni wektor położenia kamery:
uniform vec3 viewPos;
lightingShader.setVec3("viewPos", camera.Position);
Teraz, gdy mamy wszystkie wymagane zmienne, możemy obliczyć intensywność światła zwierciadlanego. Najpierw definiujemy wartość intensywności refleksu, aby nadać mu kolor o średniej jasności, tak aby nie miał on zbyt dużego wpływu:
float specularStrength = 0.5;
Gdybyśmy ustawili tę zmienną na 1.0f, otrzymalibyśmy naprawdę jasny komponent lustrzany, który jest trochę za duży dla koralowej kostki. W kolejnym tutorialu porozmawiamy o właściwym ustawieniu wszystkich tych intensywności oświetlenia i ich wpływie na obiekty. Następnie obliczamy wektor kierunku widoku i odpowiadający wektor odbicia wzdłuż osi normalnej:
vec3 viewDir = normalize(viewPos - FragPos);
vec3 reflectDir = reflect(-lightDir, norm);
Zauważ, że negujemy wektor lightDir. Funkcja reflect oczekuje, że pierwszy wektor wskazuje od źródła światła w kierunku położenia fragmentu, ale wektor lightDir wskazuje obecnie odwrotnie - od fragmentu w kierunku źródła światła (zależy to od kolejności odejmowania, kiedy obliczyliśmy wektor lightDir). Aby upewnić się, że otrzymamy poprawny wektor odbicia, odwracamy jego kierunek, najpierw negując wektor lightDir. Drugi argument oczekuje wektora normalnego, więc dostarczamy znormalizowany wektor norm.
To, co pozostało do zrobienia, to faktyczne obliczenie składnika lustrzanego. Osiąga się to za pomocą następującej formuły:
float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;
Najpierw obliczamy iloczyn skalarny między kierunkiem widoku a kierunkiem odbicia (i upewniamy się, że nie jest ujemny), a następnie podnosimy go do potęgi 32. Ta wartość 32 jest wartością połysku (ang. shininess). Im wyższa wartość połysku obiektu, tym bardziej odbija światło, zamiast rozpraszać je dookoła, a tym samym rozbłysk staje się mniejszy. Poniżej możesz zobaczyć obraz, który pokazuje wizualny wpływ różnych wartości połysku:

Nie chcemy, aby komponent lustrzany był zbyt dominujący, więc wykładnik utrzymujemy na poziomie 32. Pozostaje tylko dodać go do składowych otoczenia i rozproszenia i pomnożyć połączony wynik z kolorem obiektu:
vec3 result = (ambient + diffuse + specular) * objectColor;
FragColor = vec4(result, 1.0);
Obliczyliśmy teraz wszystkie elementy oświetlenia modelu oświetlenia Phong’a. Na podstawie ustawień twojej wirtualnej kamery powinieneś zobaczyć coś takiego:
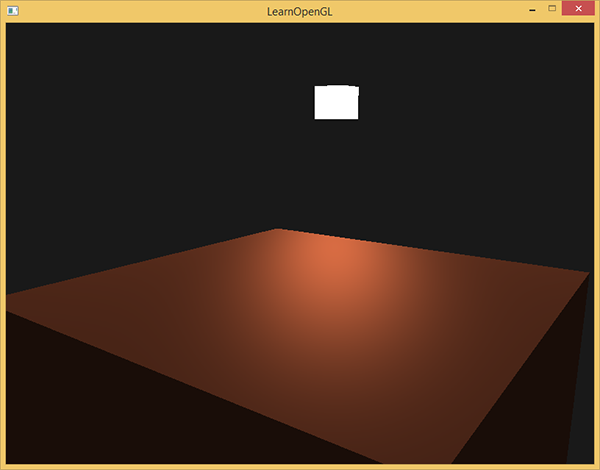
Możesz znaleźć pełny kod źródłowy aplikacji tutaj.
We wcześniejszych czasach shader’ów oświetlenia, programiści stosowali model oświetlenia Phong’a w Vertex Shader. Zaletą wykonania oświetlenia w Vertex Shader jest to, że jest on o wiele bardziej wydajny, ponieważ generalnie jest dużo mniej wierzchołków niż fragmentów, więc (kosztowne) obliczenia oświetlenia są wykonywane rzadziej. Jednak wynikowa wartość koloru w Vertex Shader to wynikowy kolor oświetlenia tylko tego wierzchołka, a wartości kolorów otaczających fragmentów są wynikiem interpolowanych kolorów oświetlenia. Rezultatem było to, że oświetlenie nie było zbyt realistyczne, chyba że użyto dużych ilości wierzchołków:

Kiedy model oświetlenia Phong’a jest implementowany w Vertex Shader, nazywa się go cieniowaniem Gourauda zamiast cieniowaniem Phong’a. Zauważ, że z powodu interpolacji oświetlenie wygląda nieco inaczej. Cieniowanie Phong’a daje bardziej wygładzone efekty oświetleniowe.
Pewnie już zauważyłeś, jak potężne są shadery. Przy użyciu niewielu informacji shader’y są w stanie obliczyć, jak światło wpływa na kolory fragmentów dla wszystkich naszych obiektów. W kolejnych tutorialach zagłębimy się w to, co możemy zrobić z modelem oświetlenia.
Ćwiczenia
- W tej chwili źródłem światła jest nudne, statyczne źródło światła, które się nie porusza. Spróbuj przesuwać źródło światła wokół sceny w czasie, używając funkcji sin lub cos. Oglądanie zmiany oświetlenia w czasie daje dobre zrozumienie modelu oświetlenia Phonga: rozwiązanie.
- Pobaw się z różnymi intensywnościami światła otoczenia, rozproszenia i lustrzanego i zobacz, jak wpływają one na wynik. Eksperymentuj także z czynnikiem połysku. Postaraj się zrozumieć, dlaczego pewne wartości mają określony efekt wizualny.
- Wykonaj cieniowanie Phong’a w przestrzeni widoku zamiast w przestrzeni świata: rozwiązanie.
- Zaimplementuj cieniowanie Gouraud zamiast cieniowania Phong’a. Jeśli zrobiłeś to dobrze, oświetlenie powinno wyglądać na przygaszone (zwłaszcza rozbłyski). Spróbuj wyjaśnić, dlaczego wygląda to dziwnie: rozwiązanie.