This is the Polish translation of Lighting/Light-casters article of learnopengl.com tutorial series.

Wszystkie dotychczasowe oświetlenie pochodzi z jednego źródła, które jest pojedynczym punktem w przestrzeni. Daje to dobre wyniki, ale w świecie rzeczywistym mamy kilka rodzajów światła, z których każdy działa inaczej. W tym samouczku omówimy kilka różnych typów świateł. Nauczenie się symulacji różnych źródeł światła jest kolejnym narzędziem, które pozwoli na dalsze wzbogacenie wirtualnego środowiska.

Najpierw omówimy światło kierunkowe, potem światło punktowe, które jest rozszerzeniem tego, co mieliśmy wcześniej, a na końcu omówimy reflektory. W następnym samouczku umieścimy te różne typy świateł na jednej scenie.

Światło kierunkowe

Kiedy źródło światła jest daleko, promienie światła pochodzące ze źródła światła są praktycznie do siebie równoległe. Wygląda to tak, jakby wszystkie promienie światła miały ten sam kierunek, niezależnie od tego, gdzie znajduje się obiekt i/lub kamera. Kiedy modelowane jest źródło światła, które ma być nieskończenie odległe, nazywa się je światłem kierunkowym (ang. directional light), ponieważ wszystkie jego promienie światła mają ten sam kierunek; jest to niezależne od lokalizacji źródła światła w przestrzeni.

Doskonałym przykładem kierunkowego źródła światła jest Słońce. Słońce nie jest nieskończenie daleko od nas, ale jest tak daleko, że możemy postrzegać je jako nieskończenie odległe w obliczeniach oświetlenia. Wszystkie promienie światła pochodzące od Słońca są następnie modelowane jako równoległe promienie świetlne, jak to widać na poniższym obrazie:

Ponieważ wszystkie promienie światła są równoległe, nie ma znaczenia, jak każdy obiekt odnosi się do położenia źródła światła, ponieważ kierunek światła pozostaje taki sam dla każdego obiektu w scenie. Ponieważ wektor kierunkowy światła pozostaje taki sam, obliczenia oświetlenia będą podobne dla każdego obiektu na scenie.

Możemy zamodelować takie kierunkowe światło, definiując wektor kierunku światła zamiast wektora położenia. Obliczenia w shaderze pozostają w większości takie same, z tą różnicą, że teraz bezpośrednio wykorzystujemy wektor kierunku światła direction zamiast obliczać wektor lightDir z wektora pozycji źródła światła:

    struct Light {
        // vec3 position; // No longer necessery when using directional lights.
        vec3 direction;

        vec3 ambient;
        vec3 diffuse;
        vec3 specular;
    };
    ...
    void main()
    {
      vec3 lightDir = normalize(-light.direction);
      ...
    }

Zauważ, że najpierw negujemy wektor light.direction. Obliczenia oświetlenia, które stosowaliśmy do tej pory, przewidywały, że kierunek światła jest kierunkiem od fragmentu w kierunku źródła światła, ale ludzie na ogół wolą określać światło kierunkowe jako globalny kierunek wskazujący od źródła światła. Dlatego musimy negować globalny wektor kierunku światła, aby zmienić jego kierunek; jest to wektor kierunkowy skierowany w stronę źródła światła. Należy również znormalizować ten wektor, ponieważ nierozsądnie jest przyjąć, że wektor wejściowy jest wektorem jednostkowym.

Powstały wektor lightDir jest następnie używany jak poprzednio w obliczeniach komponentu rozproszonego i lustrzanego.

Aby wyraźnie pokazać, że światło kierunkowe ma ten sam efekt na wszystkich obiektach, powróćmy do sceny kontenerów z końca samouczka Układy współrzędnych. W przypadku, gdy ominąłeś ten tutorial, najpierw zdefiniowaliśmy 10 różnych pozycji kontenera i wygenerowaliśmy inną macierz modelu na każdy pojemnik, gdzie każda macierz modelu zawiera odpowiednie transformacje:

    for(unsigned int i = 0; i < 10; i++)
    {
        glm::mat4 model;
        model = glm::translate(model, cubePositions[i]);
        float angle = 20.0f * i;
        model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
        lightingShader.setMat4("model", model);

        glDrawArrays(GL_TRIANGLES, 0, 36);
    }

Nie zapomnij również podać kierunku źródła światła (pamiętaj, że definiujemy kierunek jako kierunek od źródła światła; możesz zauważyć, że kierunek światła jest skierowany w dół):

    lightingShader.setVec3("light.direction", -0.2f, -1.0f, -0.3f); 	    

Przez jakiś czas przekazywaliśmy kierunki położenia i kierunku światła jako vec3, ale niektórzy ludzie wolą utrzymywać wszystkie wektory zdefiniowane jako vec4. Przy definiowaniu wektorów pozycji jako vec4 ważne jest ustawienie komponentu w na 1.0, aby operacje translacji i projekcji były poprawnie stosowane. Jednakże, definiując wektor kierunkowy jako vec4, nie chcemy, aby operacja translacji miała efekt (ponieważ reprezentuje tylko kierunek i nic więcej), więc ustawiamy komponent w na wartość 0.0.

Wektory kierunkowe są następnie reprezentowane tak: vec4 (0.2f, 1.0f, 0.3f, 0.0f). Może to również działać jako łatwe sprawdzenie dla typów światła: możesz sprawdzić, czy komponent w jest równy 1.0, aby zobaczyć, czy mamy teraz wektor pozycji światła, a jeśli w jest równe 0.0 to mamy wektor kierunku światła, więc na podstawie tego możemy dostosować obliczenia:

    if(lightVector.w == 0.0) // uwaga: uważaj na błędy zmiennoprzecinkowe
      // wykonaj obliczenia dla kierunkowego źródła światła
    else if(lightVector.w == 1.0)
      // wykonaj obliczenia światła używając pozycji światła (jak np. w ostatnim tutorialu)

Ciekawostka: tak to było robione w starej wersji OpenGL (stały potok renderingu), żeby sprawdzić z jakim typem światła miało się do czynienia - czy było to światło kierunkowe czy np. punktowe i na tej podstawie dokonywano obliczeń.

Jeśli teraz skompilujesz aplikację i obejrzysz scenę, zobaczysz, że światło kierunkowe rzuca światło na wszystkie obiekty (tak jakby były oświetlane przez Słońce). Czy widzisz, że światło rozproszone i lustrzane reagują tak, jakby na niebie znajdowało się źródło światła? Powinno to wyglądać mniej więcej tak:

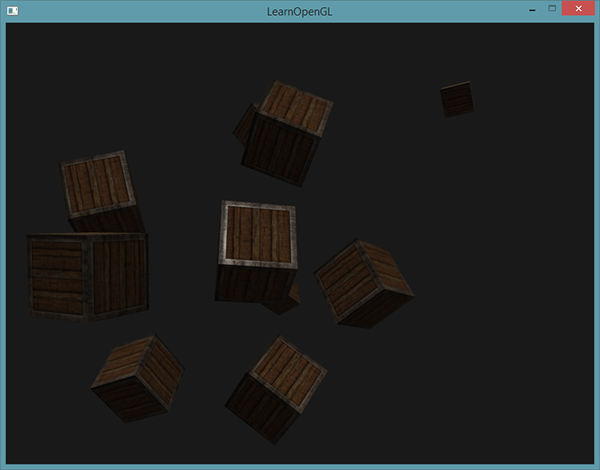
Możesz znaleźć pełny kod źródłowy aplikacji tutaj.

Światło punktowe

Światła kierunkowe doskonale nadają się by spełniać rolę globalnych świateł, które oświetlają całą scenę, ale oprócz światła kierunkowego zazwyczaj potrzebujemy również kilku świateł punktowych (ang. point light) rozrzuconych po całej scenie. Światło punktowe jest źródłem światła o danej pozycji, gdzieś w świecie, który świeci we wszystkich kierunkach, gdzie promienie światła znikają wraz z odległością. Pomyśl o żarówkach i pochodniach, które działają jak światła punktowe.

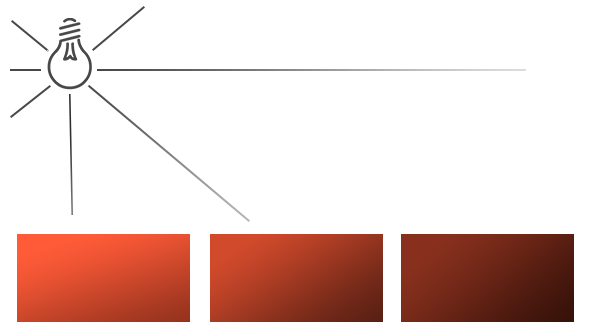
We wcześniejszych samouczkach przez cały czas pracowaliśmy z (uproszczonym) światłem punktowym. Mieliśmy źródło światła w danej pozycji, które rozprasza światło we wszystkich kierunkach z danej pozycji światła. Jednak źródło światła, które zdefiniowaliśmy rzucało promienie które nigdy nie zanikały, dzięki czemu wyglądało na to, że źródło światła jest niezwykle silne. W większości symulacji 3D chcielibyśmy zasymulować źródło światła, które oświetla tylko pewien obszar w pobliżu źródła światła, a nie całą scenę.

Jeśli dodasz 10 kontenerów do sceny z poprzedniego tutoriala, zauważysz, że pojemniki z tyłu są oświetlone z taką samą intensywnością jak pojemnik przed lampą; nie ma zdefiniowanej formuły, która redukuje wpływ światła wraz z odległością. Chcemy, aby pojemnik z tyłu był tylko lekko oświetlony w porównaniu do pojemników znajdujących się w pobliżu źródła światła.

Tłumienie światła

Zmniejszanie intensywności światła wraz z odległością jaką pokonuje promień światła, jest ogólnie nazywane tłumieniem (ang. attenuation). Jednym ze sposobów zmniejszenia intensywności światła wraz z odległością jest po prostu użycie równania liniowego. Takie równanie liniowo zmniejsza natężenie światła wraz z odległością, zapewniając, że obiekty bardziej odległe są mniej jasne. Jednak taka funkcja liniowa wydaje się nieco sztuczna. W świecie rzeczywistym światła są zazwyczaj dość jasne, ale jasność źródła światła szybko maleje na początku i pozostałe natężenie światła wolno maleje wraz z odległością. Potrzebujemy zatem innej formuły zmniejszania intensywności światła.

Na szczęście mądrzy ludzie już to wymyślili. Poniższa formuła oblicza wartość tłumienia w oparciu o odległość fragmentu od źródła światła, którą później mnożymy z wektorem natężenia światła:

\begin{equation} F_{att} = \frac{1.0}{K_c + K_l * d + K_q * d^2} \end{equation}

Stała $K_c$ jest zwykle ustawiana na wartość 1.0, która jest głównie po to, aby zapewnić, że wynik mianownika nigdy nie będzie mniejszy niż 1, ponieważ w przeciwnym razie zwiększyłoby to intensywność, co nie jest efektem, którego chcemy.
Składnik liniowy $K_l$ jest mnożony przez zmienną odległości, która zmniejsza intensywność w sposób liniowy.
Składnik kwadratowy $K_q$ jest mnożony przez kwadrant odległości i powoduje kwadratowy spadek intensywności źródła światła. Kwadratowy składnik będzie mniej znaczący w porównaniu do liniowego, gdy odległość jest mała, ale staje się znacznie większa niż liniowa, gdy odległość wzrasta.

Ze względu na termin kwadratowy światło będzie się zmniejszać głównie liniowo, aż odległość stanie się wystarczająco duża, aby wartość terminu kwadratowego przekroczyła termin liniowy, a następnie natężenie światła będzie zmniejszało się znacznie szybciej. Efektem jest to, że światło jest dość intensywne, gdy obiekt znajduje się w bliskim zasięgu, ale szybko traci jasność wraz z odległością i ostatecznie traci jasność, ale w wolniejszym tempie. Poniższy wykres pokazuje wpływ takiego tłumienia dla odległości równej 100:

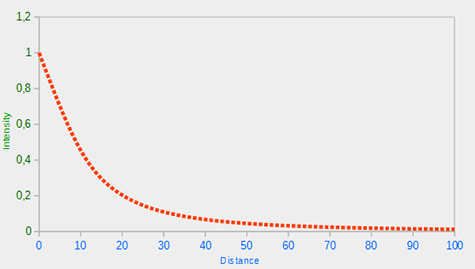
Widać, że światło ma największą intensywność, gdy odległość jest mała, ale gdy tylko odległość się zwiększy, jej intensywność jest znacznie zmniejszona i powoli osiąga wartość 0 w odległości około 100. To jest dokładnie to, czego chcemy.

Wybór właściwych wartości

Ale jak należy ustawić te 3 składniki? Ustawienie właściwych wartości zależy od wielu czynników: środowiska, promienia jaki ma obejmować światło, rodzaju światła itp. W większości przypadków jest to po prostu kwestia doświadczenia i umiarkowanej korekty. W poniższej tabeli przedstawiono niektóre z wartości, jakie te terminy mogłyby przyjąć, aby zasymulować realistyczne (prawie) źródło światła, które obejmuje określony promień (odległość). Pierwsza kolumna określa odległość, jaką światło będzie obejmować z określonymi warunkami. Wartości te są dobrym punktem wyjścia dla większości świateł (dzięki uprzejmości Wiki Ogre3D):

Dystans	$K_c$	$K_l$	$K_q$
7	1.0	0.7	1.8
13	1.0	0.35	0.44
20	1.0	0.22	0.20
32	1.0	0.14	0.07
50	1.0	0.09	0.032
65	1.0	0.07	0.017
100	1.0	0.045	0.0075
160	1.0	0.027	0.0028
200	1.0	0.022	0.0019
325	1.0	0.014	0.0007
600	1.0	0.007	0.0002
3250	1.0	0.0014	0.000007

Jak widać stały składnik $K_c$ jest utrzymywany na poziomie 1.0 we wszystkich przypadkach. Składnik liniowy $K_l$ jest zwykle dość mały, aby objąć większe odległości, a wyrażenie kwadratowe $K_q$ jest jeszcze mniejsze. Spróbuj trochę poeksperymentować z tymi wartościami, aby zobaczyć ich wpływ na wynik końcowy. W naszej scenie odległość od 32 do 100 będzie wystarczająca dla większości świateł.

Implementacja tłumienia

Aby zaimplementować tłumienie, potrzebujemy 3 dodatkowych wartości w Fragment Shader: stałą, liniową i kwadratową zmienną formuły tłumienia. Najlepiej przechowywać je w strukturze Light, którą zdefiniowaliśmy wcześniej. Zwróć uwagę, że obliczamy lightDir, tak jak to robiliśmy w poprzednim samouczku, a nie jak we wcześniejszej sekcji Directional Light.

    struct Light {
        vec3 position;  

        vec3 ambient;
        vec3 diffuse;
        vec3 specular;

        float constant;
        float linear;
        float quadratic;
    }; 

Następnie ustawiamy te zmienne w OpenGL: chcemy, aby światło obejmowało odległość 50, więc użyjemy odpowiednich wartości zmiennych stałej, liniowej i kwadratowej z tabeli:

    lightingShader.setFloat("light.constant",  1.0f);
    lightingShader.setFloat("light.linear",    0.09f);
    lightingShader.setFloat("light.quadratic", 0.032f);	    

Implementacja tłumienia w Fragment Shader jest względnie prosta: po prostu obliczamy wartość tłumienia w oparciu o formułę i mnożymy ją z kolorami otoczenia, rozproszenia i odbicia.

Potrzebujemy jednak odległości do źródła światła, aby formuła działała; pamiętasz, jak możemy obliczyć długość wektora? Możemy uzyskać wartość odległości, odejmując wektor pozycji fragmentu od wektora pozycji źródła światła. Możemy użyć wbudowanej funkcji GLSL length:

    float distance    = length(light.position - FragPos);
    float attenuation = 1.0 / (light.constant + light.linear * distance + 
        		    light.quadratic * (distance * distance));    

Następnie uwzględniamy tę wartość tłumienia w obliczeniach oświetlenia poprzez pomnożenie wartości tłumienia przez kolory otoczenia, rozproszenia i odbicia.

Moglibyśmy zostawić komponent otoczenia w spokoju, aby oświetlenie otoczenia nie malało wraz z odległością, ale gdybyśmy mieli użyć więcej niż 1 źródło światła, wszystkie komponenty otoczenia zaczną się dodawać, więc w tym przypadku chcemy również osłabić oświetlenie otoczenia. Po prostu pobaw się zmiennymi tak, aby najlepiej pasowały w twojej scenie.

    ambient  *= attenuation; 
    diffuse  *= attenuation;
    specular *= attenuation;   

Jeśli uruchomisz aplikację, otrzymasz coś takiego:

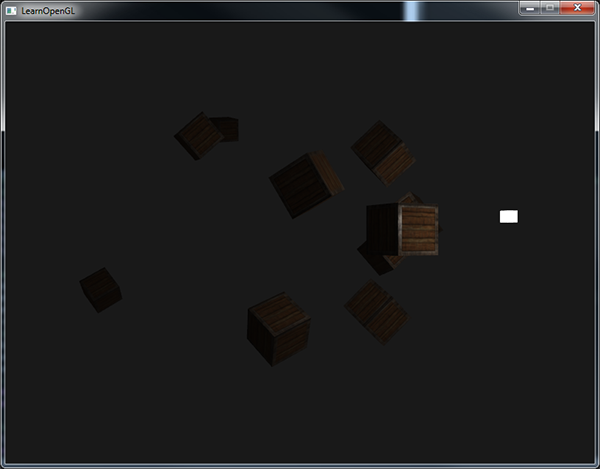
Widać teraz, że tylko przednie pojemniki są oświetlone, a najbliższy kontener jest najjaśniejszy. Pojemniki z tyłu nie są w ogóle oświetlone, ponieważ znajdują się zbyt daleko od źródła światła. Możesz znaleźć kod źródłowy aplikacji tutaj.

Światło punktowe jest zatem źródłem światła o konfigurowalnej pozycji i wartości tłumienia zastosowanym do obliczeń oświetlenia. Jest to kolejny rodzaj światła w naszym arsenale oświetlenia.

Reflektor

Ostatnim rodzajem światła, które omówimy, jest reflektor (ang. spotlight). Reflektor jest źródłem światła, które zamiast rzucać promienie światła we wszystkie kierunki, rzuca je tylko w określonym kierunku. Efekt jest taki, że oświetlane są tylko obiekty, które znajdują się w obrębie stożka reflektora. Dobrym przykładem reflektora może być latarnia uliczna lub latarka.

Reflektor w OpenGL jest reprezentowany przez położenie w przestrzeni świata, kierunek i kąt odcięcia (ang. cutoff), który określa promień reflektora. Dla każdego fragmentu obliczamy, czy fragment znajduje się pomiędzy wektorami, które definiują kąt odcięcia światła reflektorowego (a więc znajdują się w jego stożku). Jeśli tak, to odpowiednio cieniujemy ten fragment. Poniższy obraz przedstawia sposób działania reflektora:

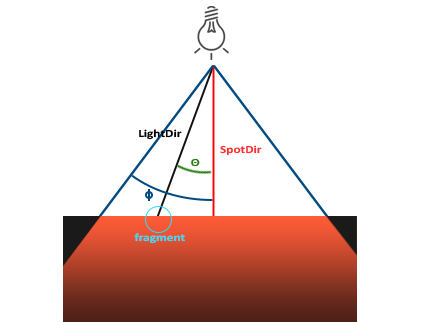
LightDir: wektor wskazujący od fragmentu do źródła światła.
SpotDir: kierunek, w którym jest skierowany reflektory.
Phi $\phi$: kąt odcięcia określający promień reflektora. Wszystko poza tym kątem nie jest oświetlone przez reflektor.
Theta $\theta$: kąt między wektorem LightDir a wektorem SpotDir. Wartość $\theta$ powinna być mniejsza niż wartość $\phi$.

Więc to, co musimy zrobić, to obliczyć iloczyn skalarny (zwraca cosinus kąta między dwoma wektorami jednostkowymi) pomiędzy wektorem LightDir, a wektorem SpotDir i porównać go z kątem odcięcia $\phi$. Teraz, gdy (w pewnym sensie) rozumiesz, jak działa światło reflektorowe, to stworzymy je w formie latarki.

Latarka

Latarka jest reflektorem umieszczonym w pozycji widza i zwykle skierowaną prosto z perspektywy gracza. Zasadniczo latarka jest normalnym światłem reflektorowym, ale jego pozycja i kierunek są stale aktualizowane w zależności od pozycji gracza i jego orientacji.

Wartości, których potrzebujemy do Fragment Shader, to wektor położenia reflektora (do obliczenia wektora kierunku światła), wektor kierunkowy reflektora i kąt odcięcia. Możemy przechowywać te wartości w strukturze Light:

    struct Light {
        vec3  position;
        vec3  direction;
        float cutOff;
        ...
    };    

Następnie przekazujemy odpowiednie wartości do shader’a:

    lightingShader.setVec3("light.position",  camera.Position);
    lightingShader.setVec3("light.direction", camera.Front);
    lightingShader.setFloat("light.cutOff",   glm::cos(glm::radians(12.5f)));

Jak widać, nie ustawiamy wartości kąta odcięcia, ale obliczamy wartość cosinusa na podstawie kąta i przekazujemy wynik cosinusa do Fragment Shader. Powodem tego jest to, że w Fragment Shader obliczamy iloczyn skalarny między wektorem LightDir i SpotDir, a iloczyn skalarny zwraca wartość cosinusa, a nie kąt, więc nie możemy bezpośrednio porównać kąta z wartością cosinusa. Aby uzyskać kąt, musimy obliczyć odwrotność wyniku cosinusa iloczynu skalarnego, który jest kosztowną operacją. Aby zaoszczędzić trochę mocy obliczeniowej, obliczamy cosinus o danym kącie odcięcia i przekazujemy ten wynik do Fragment Shader’a. Ponieważ oba kąty są teraz reprezentowane jako cosinusy, możemy je bezpośrednio porównywać bez żadnych kosztownych operacji.

Teraz pozostaje tylko obliczyć wartość theta $\theta$ i porównać ją z wartością odcięcia $\phi$, aby ustalić, czy znajdujemy się w stożku reflektora, czy poza nim:

    float theta = dot(lightDir, normalize(-light.direction));

    if(theta > light.cutOff) 
    {       
      // wykonaj obliczenia oświetlenia
    }
    else  // w przeciwynym wypadku, użyj światła otoczenia, aby scena poza swiatłem reflektora nie była całkowicie ciemna.
      color = vec4(light.ambient * vec3(texture(material.diffuse, TexCoords)), 1.0);

Najpierw obliczamy iloczyn skalarny między wektorem lightDir i zanegowanym wektorem direction (zanegowanym, ponieważ chcemy, aby wektor był skierowany do źródło światła, zamiast od niego). Pamiętaj, aby znormalizować wszystkie wektory.

Możesz się zastanawiać, dlaczego zamiast znaku < w warunku if znajduje się znak >. Czy theta nie powinna być mniejsza niż wartość cosinusa kąta odcięcia, aby znajdowała się w stożku reflektora? Zgadza się, ale nie zapominaj, że wartości kątów są reprezentowane jako wartości cosinusów, a kąt 0 jest reprezentowany jako wartość cosinusowa 1.0, podczas gdy kąt 90 stopni jest reprezentowany jako wartość cosinusowa 0.0 jak widać na tym rysunku:

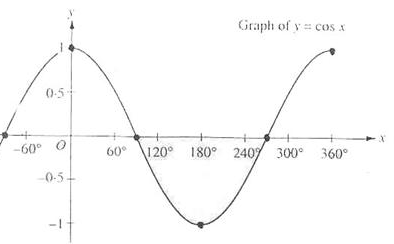
Teraz możesz zobaczyć, że im wartość cosinusa jest bliższa 1.0, tym mniejszy jest kąt. Teraz ma to sens, dlaczego theta musi być większa niż wartość cosinusa kąta odcięcia. Wartość kąta odcięcia jest obecnie ustawiona na 12.5, co po operacji cosinusa jest równe 0.9978, więc wartość cosinusa theta między 0.9979 a 1.0 spowodowałaby oświetlenie fragmentu w stożku reflektora.

Uruchomianie aplikacji spowoduje oświetlenie fragmentów, które znajdują się bezpośrednio w stożku reflektora. Powinno to wyglądać mniej więcej tak:

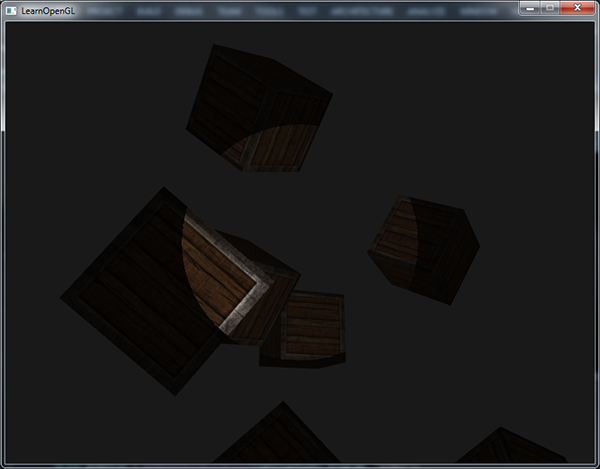
Możesz znaleźć pełny kod źródłowy tutaj.

Nadal wygląda to jednak trochę sztucznie, głównie dlatego, że reflektor ma ostre krawędzie. Wszędzie tam, gdzie oświetlone fragment znajdują się na krawędzi stożka reflektora, wyłącza się go gwałtownie, zamiast tworzyć płynne przejście do zaniknięcia oświetlenia. Realistyczny reflektor zmniejszyłby stopniowo światło im bliżej jego krawędzi.

Gładkie/miękkie krawędzie

Aby stworzyć gładkie krawędzie reflektora, chcemy zasymulować światło reflektora, który posiada wewnętrzny (ang. inner) i zewnętrzny (ang. outer) stożek. Możemy ustawić wewnętrzny stożek jako stożek zdefiniowany w poprzedniej sekcji, ale chcemy również dodać zewnętrzny stożek, który stopniowo przyciemnia światło od krawędzi wewnętrznego stożka do krawędzi zewnętrznego stożka.

Aby utworzyć zewnętrzny stożek, po prostu definiujemy inną wartość cosinusa, która reprezentuje kąt między wektorem kierunkowym światła reflektora a wektorem zewnętrznym stożka (równym jego promieniowi). Następnie, jeśli fragment znajduje się między stożkiem wewnętrznym a zewnętrznym, należy obliczyć wartość intensywności między 0.0 a 1.0. Jeśli fragment znajduje się wewnątrz stożka wewnętrznego, jego intensywność jest równa 1.0, jeśli fragment znajduje się poza zewnętrznym stożkiem to jego intensywność jest równa 0.0.

Możemy obliczyć taką wartość za pomocą następującego wzoru:

\begin{equation} I = \frac{\theta - \gamma}{\epsilon} \end{equation}

Tutaj $\epsilon$ (epsilon) to cosinusowa różnica między wewnętrznym ($\phi$) i zewnętrznym stożkiem ($\gamma$) ($\epsilon = \phi - \gamma$). Wynikowa wartość $I$ jest wtedy intensywnością światła reflektora dla bieżącego fragmentu.

Trochę trudno jest sobie wyobrazić, jak ta formuła działa, więc przetestujmy ją z kilkoma przykładowymi wartościami:

$\theta$	$\theta$ w stopniach	$\phi$ (kąt wew. stożka)	$\phi$ w stopniach	$\gamma$ (kąt zew. stożka)	$\gamma$ w stopniach	$\epsilon$	$I$
0.87	30	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.87 - 0.82 / 0.09 = 0.56
0.9	26	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.9 - 0.82 / 0.09 = 0.89
0.97	14	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.97 - 0.82 / 0.09 = 1.67
0.83	34	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.83 - 0.82 / 0.09 = 0.11
0.64	50	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.64 - 0.82 / 0.09 = -2.0
0.966	15	0.9978	12.5	0.953	17.5	0.9978 - 0.953 = 0.0448	0.966 - 0.953 / 0.0448 = 0.29

Jak widać, w zasadzie interpolujemy pomiędzy wartością zewnętrznego cosinusa i wartością wewnętrznego cosinusa w oparciu o wartość $\theta$. Jeśli nadal nie widzisz, co się dzieje, nie martw się, możesz po prostu przyjąć formułę za pewnik i wrócić tutaj, gdy będziesz starszy i mądrzejszy.

Ponieważ mamy teraz wartość intensywności, która jest albo ujemna, gdy znajduje się poza światłem reflektora, albo wyższa niż 1.0, gdy znajduje się wewnątrz wewnętrznego stożka i gdzieś pomiędzy krawędziami. Jeśli właściwie “obetniemy” (ang. clamp) wartości, nie będziemy potrzebować warunku if-else w Fragment Shader i możemy po prostu pomnożyć składniki światła z obliczoną wartością intensywności:

    float theta     = dot(lightDir, normalize(-light.direction));
    float epsilon   = light.cutOff - light.outerCutOff;
    float intensity = clamp((theta - light.outerCutOff) / epsilon, 0.0, 1.0);    
    ...
    // pozostawiamy światło otoczenia niezmienione, aby zawsze mieć trochę światła.
    diffuse  *= intensity;
    specular *= intensity;
    ...

Zauważ, że używamy funkcji clamp, która obcina daną wartość do zadanego zakresu wartości 0.0 i 1.0. Dzięki temu wartości intensywności nie znajdą się poza przedziałem [0, 1].

Upewnij się, że dodałeś outerCutOff do struktury Light i ustawiasz jej uniform w aplikacji. Dla poniższego obrazu zastosowano wewnętrzny kąt odcięcia 12.5 i zewnętrzny kąt odcięcia 17.5:

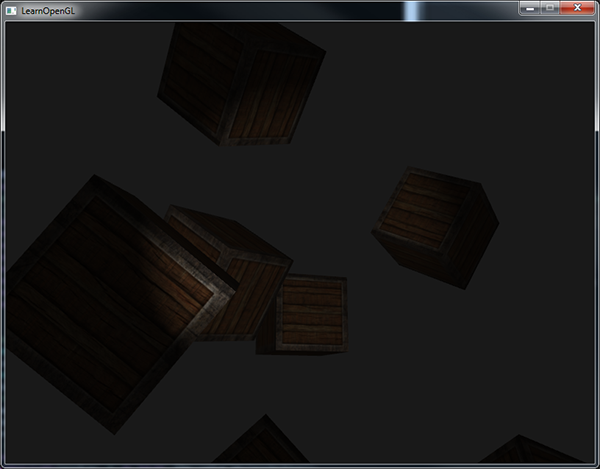
Ahhh, jest znacznie lepiej. Pobaw się z wewnętrznymi i zewnętrznymi kątami odcięcia i spróbuj stworzyć reflektor, który będzie lepiej pasował do twoich potrzeb. Możesz znaleźć kod źródłowy aplikacji tutaj.

Światło typu latarka/reflektor jest idealne do gier typu horror, a w połączeniu ze światłami kierunkowymi i punktowymi środowisko naprawdę zaczyna świecić. W następnym samouczku połączymy wszystkie światła i triki, które omawialiśmy do tej pory.

Ćwiczenia

Spróbuj poeksperymentować ze wszystkimi różnymi rodzajami światła i Frgament Shader’ami. Spróbuj odwrócić niektóre wektory i/lub użyć < zamiast >. Spróbuj wyjaśnić uzyskane efekty wizualne.

Typy świateł

LearnOpenGL.com