This is the Polish translation of Advanced-OpenGL/Geometry-Shader article of learnopengl.com tutorial series.
Pomiędzy Vertex Shader a Fragment Shader znajduje się opcjonalny etap cieniujący nazywany
Rzucimy cię prosto na głęboką wodę, pokazując przykład shadera geometrii:
#version 330 core
layout (points) in;
layout (line_strip, max_vertices = 2) out;
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
}
Na początku każdego Geometry Shadera musimy zadeklarować typ prymitywu na wejściu, który otrzymujemy z Vertex Shadera. Robimy to, poprzez kwalifikator layout przed słowem kluczowym
points: podczas rysowania prymitywów GL_POINTS (1).lines: podczas rysowania GL_LINES lub GL_LINE_STRIP (2).lines_adjacency: GL_LINES_ADJACENCY lub GL_LINE_STRIP_ADJACENCY (4).triangles: GL_TRIANGLES, GL_TRIANGLE_STRIP lub GL_TRIANGLE_FAN (3).triangles_adjacency: GL_TRIANGLES_ADJACENCY lub GL_TRIANGLE_STRIP_ADJACENCY (6).
Są to prawie wszystkie prymitywy, które możemy przekazać do wywoływania wywołań renderowania takich jak triangles. Liczba w nawiasie reprezentuje minimalną liczbę wierzchołków zawartych w pojedynczym prymitywie.
Następnie musimy również określić typ prymitywu, który będzie generowany przez Geometry Shader, i robimy to za pomocą kwalifikatora układu przed słowem kluczowym
pointsline_striptriangle_strip
Dzięki tym 3 kwalifikatorom wyjściowym możemy stworzyć niemal dowolny kształt z prymitywów wejściowych. Aby na przykład wygenerować pojedynczy trójkąt, określilibyśmy triangle_strip jako wynik, a następnie wyprowadzilibyśmy 3 wierzchołki.
Geometry Shader oczekuje również od nas ustawienia maksymalnej liczby wyprowadzanych wierzchołków (jeśli przekroczysz tę liczbę, OpenGL nie narysuje dodatkowych wierzchołków), co możemy również zrobić za pomocą kwalifikatora układu słowa kluczowego line_strip z maksymalną liczbą 2 wierzchołków.
W przypadku, gdy zastanawiasz się, co to jest line_strip: jest to łamana, która łączy razem zestaw punktów, tworząc jedną ciągłą linię między nimi (minimum 2 punktami). Każdy dodatkowy punkt dany do renderowania spowoduje powstanie nowej linii między nowym punktem a poprzednim punktem, jak widać na poniższym obrazku, na którym mamy 5 wierzchołków:
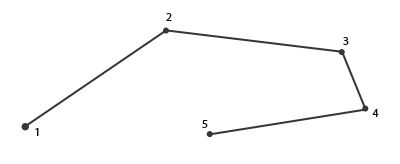
Przy obecnym shaderze będziemy generować tylko jedną linię, ponieważ maksymalna liczba wierzchołków jest równa 2.
Aby wygenerować sensowne wyniki, potrzebujemy sposobu na pobranie danych wyjściowych z poprzedniego shadera. GLSL daje nam
in gl_Vertex
{
vec4 gl_Position;
float gl_PointSize;
float gl_ClipDistance[];
} gl_in[];
Tutaj jest zadeklarowana jako
Zauważ, że jest zadeklarowany jako tablica, ponieważ większość prymitywów renderowania składa się z więcej niż jednego wierzchołka, a Geometry Shader otrzymuje wszystkie wierzchołki prymitywu jako dane wejściowe.
Korzystając z danych wierzchołkowych z Vertex Shadera, możemy zacząć generować nowe dane, które są wykonywane za pomocą 2 funkcji Geometry Shadera o nazwie
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
}
Za każdym razem, gdy wywołujemy
Teraz, gdy wiesz (trochę), jak działają shadery geometrii, możesz prawdopodobnie zgadnąć, co robi ten shader geometrii. Ten Geometry Shader przyjmuje jako element wejściowy prymityw punktu i tworzy łamaną poziomą z wejściowym wierzchołkiem jako środkiem. Jeśli to wyrenderujemy, to będzie to wyglądać tak:
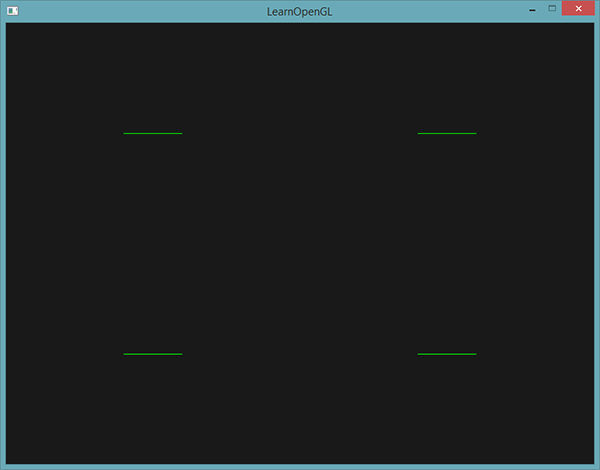
Niezbyt imponujące, ale warto wziąć pod uwagę, że dane wyjściowe zostały wygenerowane za pomocą następującego wywołania:
glDrawArrays(GL_POINTS, 0, 4);
Chociaż jest to stosunkowo prosty przykład, pokazuje, w jaki sposób możemy używać shaderów geometrii do (dynamicznego) generowania nowych kształtów w locie. W dalszej części tego samouczka omówimy kilka interesujących efektów, które możemy osiągnąć za pomocą shaderów geometrii, ale na razie zaczniemy od stworzenia prostego Geometry Shadera.
Używanie Geometry Shader’ów
Aby zademonstrować użycie Geometry Shadera, stworzymy naprawdę prostą scenę, w której po prostu narysujemy 4 punkty na płaszczyźnie Z w NDC. Współrzędne punktów to:
float points[] = {
-0.5f, 0.5f, // lewy górny
0.5f, 0.5f, // prawy górny
0.5f, -0.5f, // prawy dolny
-0.5f, -0.5f // lewy dolny
};
Vertex Shader musi tylko narysować punkty na płaszczyźnie Z, więc potrzebujemy tylko podstawowego Vertex Shadera:
#version 330 core
layout (location = 0) in vec2 aPos;
void main()
{
gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0);
}
Następnie ustawimy kolor zielony dla wszystkich punktów, które mamy wpisane na sztywno w Fragment Shader:
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(0.0, 1.0, 0.0, 1.0);
}
Wygeneruj VAO i VBO dla danych wierzchołków punktów, a następnie narysuj je za pomocą
shader.use();
glBindVertexArray(VAO);
glDrawArrays(GL_POINTS, 0, 4);
Rezultatem jest ciemna scena z 4 (ledwo widocznymi) zielonymi punktami:
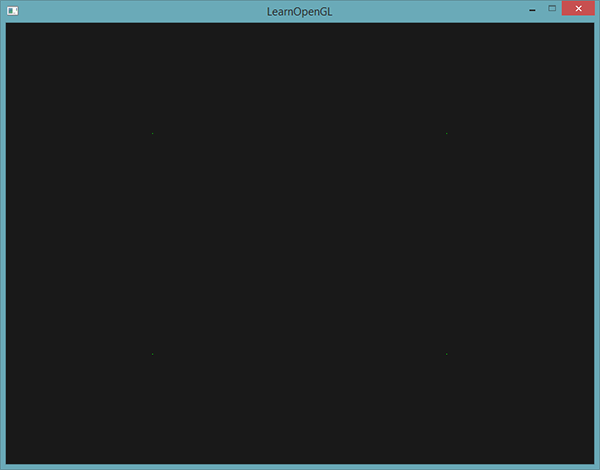
Ale czy nie nauczyliśmy się już tego wszystkiego robić? Tak, ale teraz zamierzamy urozmaicić tę małą scenę, dodając do niej shader geometrii.
Dla celów edukacyjnych stworzymy coś, co nazywa się shaderem geometrii
#version 330 core
layout (points) in;
layout (points, max_vertices = 1) out;
void main() {
gl_Position = gl_in[0].gl_Position;
EmitVertex();
EndPrimitive();
}
W tej chwili ten shader geometrii powinien być dość łatwy do zrozumienia. Po prostu emituje niezmodyfikowaną pozycję wierzchołka, którą odebrał jako dane wejściowe i generuje prymityw punktowy.
Geometry Shader musi zostać skompilowany i połączony z programem podobnie jak Vertex Shader i Fragment Shader, ale tym razem utworzymy shader przy użyciu GL_GEOMETRY_SHADER jako typu shadera:
geometryShader = glCreateShader(GL_GEOMETRY_SHADER);
glShaderSource(geometryShader, 1, &gShaderCode, NULL);
glCompileShader(geometryShader);
...
glAttachShader(program, geometryShader);
glLinkProgram(program);
Kod kompilacji shaderów jest w zasadzie taki sam jak kod Vertex Shader i Fragment Shader. Sprawdź, czy nie występują błędy kompilacji lub linkowania!
Jeśli teraz skompilujesz i uruchomisz aplikację, powinieneś zobaczyć wynik podobny do następującego:

Jest to dokładnie taki sam wynik jak bez Geometry Shadera! To trochę nudne, ale fakt, że wciąż byliśmy w stanie narysować punkty, oznacza, że shader geometrii działa, więc teraz nadszedł czas na ciekawsze efekty!
Zbudujmy kilka domków
Rysowanie punktów i linii nie jest interesujące, więc musimy być trochę kreatywni, korzystając z Geometry Shadera, aby narysować dla nas obiekt w miejscu każdego punktu. Możemy to osiągnąć, ustawiając wyjście Geometry Shadera na
Pasek trójkątów w OpenGL jest bardziej efektywnym sposobem rysowania trójkątów przy użyciu mniejszej liczby wierzchołków. Po narysowaniu pierwszego trójkąta każdy kolejny wierzchołek wygeneruje kolejny trójkąt obok pierwszego trójkąta: co 3 sąsiednie wierzchołki utworzą trójkąt. Jeśli mamy w sumie 6 wierzchołków, które tworzą pasek trójkątów, otrzymalibyśmy następujące trójkąty: (1,2,3), (2,3,4), (3,4,5) i (4,5,6) tworząc w sumie 4 trójkąty. Pasek trójkątów potrzebuje co najmniej 3 wierzchołków i wygeneruje N-2 trójkąty; z 6 wierzchołkami stworzyliśmy 6-2 = 4 trójkąty. Poniższy obraz to ilustruje:
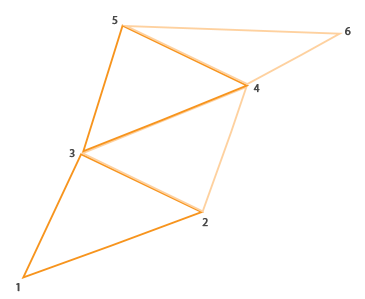
Używając paska trójkątów jako wyjścia z Geometry Shadera, możemy z łatwością stworzyć kształt domu, generując 3 sąsiednie trójkąty we właściwej kolejności. Poniższy obrazek pokazuje, w jakiej kolejności musimy narysować wierzchołki, aby uzyskać trójkąty, których potrzebujemy, gdzie niebieska kropka to punkt wejściowy:
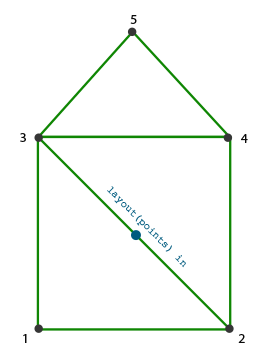
Przekłada się to na następujący kod Geometry Shadera:
#version 330 core
layout (points) in;
layout (triangle_strip, max_vertices = 5) out;
void build_house(vec4 position)
{
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1:lewy dolny
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2:prawy dolny
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3:lewy górny
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4:prawy górny
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5:górny
EmitVertex();
EndPrimitive();
}
void main() {
build_house(gl_in[0].gl_Position);
}
Ten Geometry Shader generuje 5 wierzchołków, przy czym każdy wierzchołek jest pozycją punktu plus przesunięcie, tworząc jeden duży pasek trójkątów. Wynikowy prymityw jest następnie rasteryzowany, a Fragment Shader działa na całym pasku trójkąta, co daje zielony dom dla każdego narysowanego punktu:
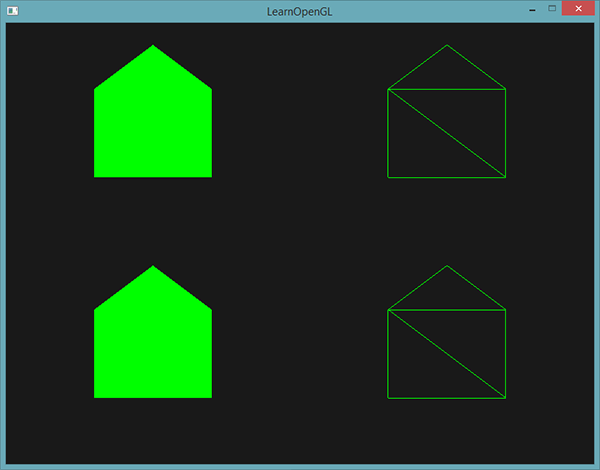
Możesz zobaczyć, że każdy dom rzeczywiście składa się z 3 trójkątów - wszystkie rysowane za pomocą tylko jednego punktu w przestrzeni. Zielone domy wyglądają trochę nudno, więc nadajmy każdemu niepowtarzalny kolor. W tym celu dodamy dodatkowy atrybut wierzchołków z informacją o kolorze na wierzchołek w Vertex Shaderze, a następnie przekażemy go do Geometry Shadera, który przekaże go dalej do Fragment Shadera.
Zaktualizowane dane wierzchołków podano poniżej:
float points[] = {
-0.5f, 0.5f, 1.0f, 0.0f, 0.0f, // lewy górny
0.5f, 0.5f, 0.0f, 1.0f, 0.0f, // prawy górny
0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // prawy dolny
-0.5f, -0.5f, 1.0f, 1.0f, 0.0f // lewy dolny
};
Następnie aktualizujemy Vertex Shader, aby przesłać atrybut koloru do Geometry Shadera za pomocą bloku interfejsu:
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;
out VS_OUT {
vec3 color;
} vs_out;
void main()
{
gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0);
vs_out.color = aColor;
}
Następnie musimy zadeklarować ten sam blok interfejsu (z inną nazwą interfejsu) w Geometry Shaderze:
in VS_OUT {
vec3 color;
} gs_in[];
Ponieważ Geometry Shader działa na zbiorze wierzchołków jako dane wejściowe, dane wejściowe z Vertex Shadera są zawsze reprezentowane jako tablice danych, mimo że mamy teraz tylko jeden wierzchołek.
Nie musimy koniecznie używać bloków interfejsu do przesyłania danych do Geometry Shadera. Mogliśmy również napisać to jako:
in vec3 vColor[];
Jeśli Vertex Shader przekazał wektor koloru jako out vec3 vColor. Bloki interfejsów są jednak o wiele łatwiejsze w obsłudze w shaderach, takich jak Geometry Shader. W praktyce wejścia Geometry Shadera mogą być dość duże, a grupowanie ich w jeden duży blok interfejsu ma dużo większy sens.
Następnie powinniśmy zadeklarować wektor koloru wyjściowego dla Fragment Shadera:
out vec3 fColor;
Ponieważ Fragment Shader oczekuje tylko jednego (interpolowanego) koloru, nie ma sensu przekazywać wielu kolorów. Wektor fColor nie jest zatem tablicą, ale pojedynczym wektorem. Podczas emitowania wierzchołka każdy wierzchołek przechowuje ostatnią przechowywaną wartość w fColor dla wykonania Fragment Shadera. W przypadku domów możemy w ten sposób wypełnić tylko fColor jednym kolorem z Vertex Shadera przed wyemitowaniem pierwszego wierzchołka, aby pokolorować cały dom:
fColor = gs_in[0].color; // gs_in[0] ponieważ istnieje tylko jeden wierzchołek wejściowy
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1:lewy dolny
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2:prawy dolny
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3:lewy górny
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4:prawy górny
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5:górny
EmitVertex();
EndPrimitive();
Wszystkie wyemitowane wierzchołki będą miały ostatnią zapisaną wartość w fColor osadzoną w ich danych, która jest równa kolorowi wierzchołka, którą zdefiniowaliśmy w ich atrybutach. Wszystkie domy będą teraz miały własny kolor:
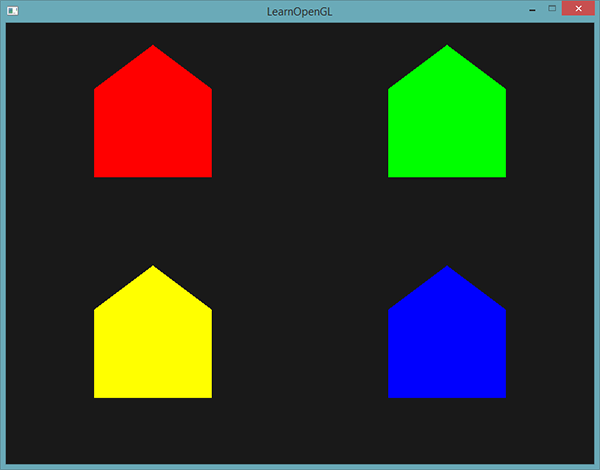
Dla zabawy mogliśmy również udawać, że jest zima i dać dachowi trochę śniegu, nadając ostatniemu wierzchołkowi własny kolor: biały.
fColor = gs_in[0].color;
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1:lewy dolny
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2:prawy dolny
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3:lewy górny
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4:prawy górny
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5:górny
fColor = vec3(1.0, 1.0, 1.0);
EmitVertex();
EndPrimitive();
Wynik wygląda teraz tak:
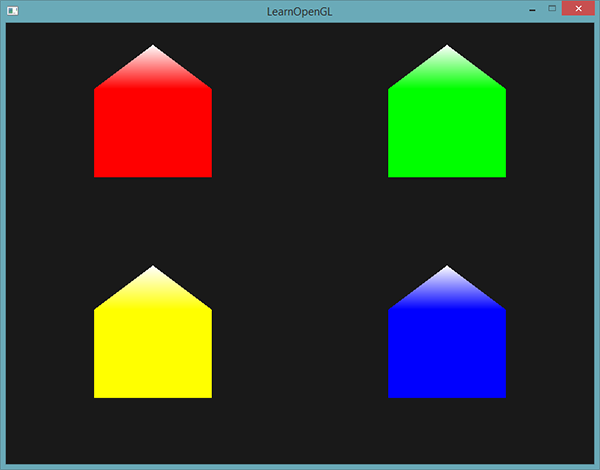
Możesz porównać swój kod źródłowy z kodem tutaj.
Widać, że za pomocą shaderów geometrii można uzyskać całkiem ciekawe rezultaty nawet z najprostszymi prymitywami. Ponieważ kształty są generowane dynamicznie na ultraszybkim sprzęcie GPU, jest to o wiele bardziej wydajne niż definiowanie tych kształtów w buforze wierzchołków. Bufory geometrii są zatem doskonałym narzędziem do optymalizacji prostych, często powtarzających się kształtów, takich jak sześciany w świecie wokseli lub liści trawy na dużej, otwartej scenie.
Wybuchające obiekty
Podczas gdy rysowanie domów jest zabawne, nie jest to coś, z czego będziemy korzystać często. Właśnie dlatego zamierzamy sprawić by obiekty eksplodowały! Jest to również coś, czego prawdopodobnie nie będziemy używać, ale pokazuje niektóre z możliwości shaderów geometrii.
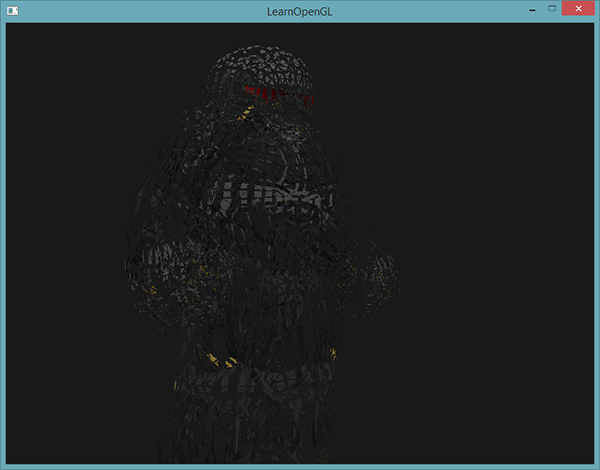
Wspaniałą cechą takiego efektu Geometry Shadera jest to, że działa na wszystkich obiektach, niezależnie od ich złożoności.
Ponieważ zamierzamy przesunąć każdy wierzchołek w kierunku wektora normalnego trójkąta, najpierw musimy obliczyć ten wektor normalny. To, co musimy zrobić, to obliczyć wektor prostopadły do powierzchni trójkąta, używając tylko 3 wierzchołków, do których mamy dostęp. Możesz pamiętać z tutoriala transformacje, że możemy pobrać wektor prostopadły do dwóch innych wektorów za pomocą funkcji
vec3 GetNormal()
{
vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
return normalize(cross(a, b));
}
Tutaj pobieramy dwa wektory a i b, które są równoległe do powierzchni trójkąta. Odejmowanie dwóch wektorów od siebie powoduje, że wektor jest różnicą dwóch wektorów, a ponieważ wszystkie 3 punkty leżą na płaszczyźnie trójkąta, odjęcie dowolnego z jego wektorów od siebie powoduje, że wektor jest równoległy do płaszczyzny. Zwróć uwagę, że jeśli zamienimy miejscami a z b w funkcji
Teraz, gdy wiemy, jak obliczyć wektor normalny, możemy utworzyć funkcję
vec4 explode(vec4 position, vec3 normal)
{
float magnitude = 2.0;
vec3 direction = normal * ((sin(time) + 1.0) / 2.0) * magnitude;
return position + vec4(direction, 0.0);
}
Sama funkcja nie powinna być zbyt skomplikowana. Funkcja -1.0 a 1.0. Ponieważ nie chcemy aby obiekt się naprawiał obcinamy wartości sin do zakresu [0,1]. Wynikowa wartość jest następnie mnożona przez wektor normal, a powstały wektor direction jest dodawany do wektora pozycji.
Pełny Geometry Shader efektu
#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices = 3) out;
in VS_OUT {
vec2 texCoords;
} gs_in[];
out vec2 TexCoords;
uniform float time;
vec4 explode(vec4 position, vec3 normal) { ... }
vec3 GetNormal() { ... }
void main() {
vec3 normal = GetNormal();
gl_Position = explode(gl_in[0].gl_Position, normal);
TexCoords = gs_in[0].texCoords;
EmitVertex();
gl_Position = explode(gl_in[1].gl_Position, normal);
TexCoords = gs_in[1].texCoords;
EmitVertex();
gl_Position = explode(gl_in[2].gl_Position, normal);
TexCoords = gs_in[2].texCoords;
EmitVertex();
EndPrimitive();
}
Zwróć uwagę, że przed wysłaniem wierzchołka wyprowadzamy również odpowiednie współrzędne tekstury.
Nie zapomnij także ustawić zmiennej time w kodzie OpenGL:
shader.setFloat("time", glfwGetTime());
Rezultatem jest model 3D, który zdaje się nieustannie eksplodować swoje wierzchołki w czasie, po czym znów wraca do normy. Chociaż nie jest to bardzo przydatne, pokazuje bardziej zaawansowane wykorzystanie Geometry Shadera. Możesz porównać swój kod źródłowy z pełnym kodem źródłowym tutaj.
Wizualizacja wektorów normalnych
W tej sekcji przedstawimy przykład użycia Geometry Shadera, który jest rzeczywiście użyteczny: wizualizacja wektorów normalnych dowolnego obiektu. Podczas programowania shaderów w końcu natrafisz na dziwne efekty wizualne, których przyczyna jest trudna do ustalenia. Częstą przyczyną błędów oświetlenia są nieprawidłowe wektory normalne spowodowane niepoprawnym ładowaniem danych wierzchołków, niewłaściwym określeniem ich jako atrybutów wierzchołków lub nieprawidłowym zarządzaniem nimi w shaderach. To, czego chcemy, to sposób na wykrycie, czy dostarczane przez nas wektory normalne są poprawne. Doskonałym sposobem sprawdzenia, czy twoje wektory normalne są poprawne, jest ich wizualizacja i tak się składa, że Geometry Shader jest niezwykle przydatnym narzędziem do tego celu.
Pomysł jest następujący: najpierw narysujemy scenę normalnie bez Geometry Shadera, a następnie narysujemy scenę po raz drugi, ale tym razem wyświetlimy jedynie wektory normalne, które generujemy za pomocą shadera geometrii. Shader geometrii przyjmuje jako dane wejściowe prymitywy trójkąta i generujemy z nich 3 linie w kierunku wektora normalnego - jeden wektor normalny dla każdego wierzchołka. W pseudokodzie będzie wyglądało to mniej więcej tak:
shader.use();
DrawScene();
normalDisplayShader.use();
DrawScene();
Tym razem tworzymy Geometry Shader, który używa wektorów normalnych dostarczonych przez model zamiast generować je samodzielnie. Aby dostosować się do skalowania i rotacji (ze względu na macierz widoku i macierz modelu) najpierw przekształcimy wektory normalne za pomocą macierzy normalnych przed przekształceniem ich na współrzędne w przestrzeni obcinania (Geometry Shader otrzymuje wektory pozycji jako współrzędne przestrzeni obcinania, więc powinniśmy również przekształcić wektory normalne do tej samej przestrzeni). Wszystko to można zrobić w Vertex Shader:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
out VS_OUT {
vec3 normal;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
mat3 normalMatrix = mat3(transpose(inverse(view * model)));
vs_out.normal = normalize(vec3(projection * vec4(normalMatrix * aNormal, 0.0)));
}
Przekształcony wektor normalny w przestrzeni obcinania jest następnie przekazywany do następnego etapu cieniowania za pośrednictwem bloku interfejsu. Następnie Geometry Shader pobiera każdy wierzchołek (z pozycją i wektorem normalnym) i rysuje wektor normalny z każdego wektora położenia:
#version 330 core
layout (triangles) in;
layout (line_strip, max_vertices = 6) out;
in VS_OUT {
vec3 normal;
} gs_in[];
const float MAGNITUDE = 0.4;
void GenerateLine(int index)
{
gl_Position = gl_in[index].gl_Position;
EmitVertex();
gl_Position = gl_in[index].gl_Position + vec4(gs_in[index].normal, 0.0) * MAGNITUDE;
EmitVertex();
EndPrimitive();
}
void main()
{
GenerateLine(0); // first vertex normal
GenerateLine(1); // second vertex normal
GenerateLine(2); // third vertex normal
}
Zawartość Geometry Shadera powinna już teraz być oczywista. Zwróć uwagę, że mnożymy normalny wektor przez wektor MAGNITUDE, aby ograniczyć rozmiar wyświetlanych wektorów normalnych (w przeciwnym razie byłyby zbyt duże).
Ponieważ wizualizacja wektorów normalnych jest najczęściej używana do celów debugowania, możemy po prostu wyświetlić je jako linie jedno-kolorowe (lub super-fantazyjne linie, jeśli masz na to ochotę) za pomocą Fragment Shadera:
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(1.0, 1.0, 0.0, 1.0);
}
Teraz renderując swój model za pomocą shadera normalnych, a następnie za pomocą specjalnego shadera wizualizującego wektory normalne, zobaczysz coś takiego:
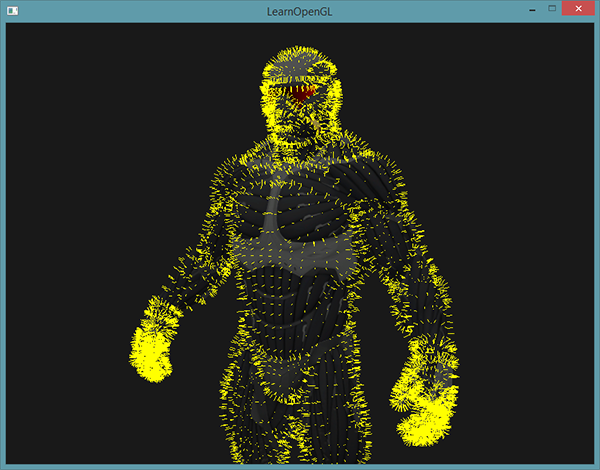
Oprócz tego, że nasz nanokombinezon wygląda teraz jak futerko, daje nam naprawdę przydatną metodę określania, czy wektory normalne modelu są rzeczywiście poprawne. Możesz sobie wyobrazić, że takie shadery geometrii są również często używane do dodawania
Możesz znaleźć pełny kod źródłowy tutaj.