This is the Polish translation of Advanced-OpenGL/Instancing article of learnopengl.com tutorial series.
Załóżmy, że masz scenę, na której rysujesz wiele modeli, w których większość z tych modeli zawiera ten sam zestaw danych wierzchołków, ale z różnymi transformacjami. Pomyśl o scenie wypełnionej liśćmi trawy: każdy liść trawy to mały model składający się tylko z kilku trójkątów. Prawdopodobnie będziesz chciał narysować ich całkiem sporo, a twoja scena może skończyć z tysiącami, a może dziesiątkami tysięcy liści traw, które musisz wyrenderować w każdej klatce. Ponieważ każdy liść składa się tylko z kilku trójkątów, liść jest renderowany niemal natychmiast, ale wszystkie te tysiące wywołań renderowania, które będziesz musiał wykonać, drastycznie zmniejszą wydajność.
Gdybyśmy faktycznie renderowali tak dużą liczbę obiektów, będzie wyglądać to mniej więcej tak:
for(unsigned int i = 0; i < amount_of_models_to_draw; i++)
{
DoSomePreparations(); // podepnij VAO, podepnij teksturę, ustaw uniformy, itp.
glDrawArrays(GL_TRIANGLES, 0, amount_of_vertices);
}
Podczas rysowania wielu
Byłoby znacznie wygodniej, gdybyśmy mogli jednorazowo wysłać dane do GPU, a następnie powiedzieć OpenGL, aby narysował wiele obiektów za pomocą jednego wywołania renderującego z wykorzystaniem tych danych. Powitajmy
Instancjonowanie to technika, w której rysujemy wiele obiektów naraz za pomocą jednego wywołania renderowania, oszczędzając nam całą komunikację CPU -> GPU za każdym razem, gdy potrzebujemy renderować obiekt; to trzeba zrobić tylko raz. Aby renderować za pomocą instancji, wystarczy zmienić wywołania renderowania
Funkcja sama w sobie jest nieco bezużyteczna. Renderowanie tego samego obiektu tysiąc razy nie ma dla nas żadnego znaczenia, ponieważ każdy z renderowanych obiektów jest dokładnie taki sam, a więc również ma tą samą transformację; widzielibyśmy tylko jeden obiekt! Z tego powodu GLSL posiada inną wbudowaną zmienną w Vertex Shader o nazwie gl_InstanceID.
Podczas rysowania za pośrednictwem jednego z wywołań renderowania instancjonowanego, gl_InstanceID jest zwiększany dla każdej renderowanej instancji począwszy od 0. Gdybyśmy mieli na przykład renderować 43-cią instancję, gl_InstanceID miałoby wartość 42 w Vertex Shader. Posiadanie unikalnej wartości dla każdej instancji oznacza, że możemy teraz na przykład indeksować dużą tablicę wartości pozycji, aby ustawić każdą instancję w innym miejscu na scenie.
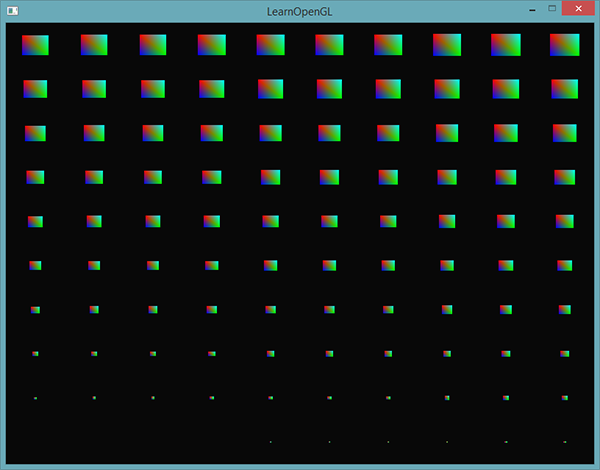
Aby uzyskać wrażenie renderowania instancjonowanego, przedstawimy prosty przykład, który renderuje sto dwuwymiarowych kwadratów w znormalizowanych współrzędnych urządzenia za pomocą tylko jednego wywołania renderowania. Osiągamy to, dodając małe przesunięcie do każdego instancjonowanego kwadratu, indeksując tablicę uniform za pomocą 100 wektorów przesunięcia. Rezultatem jest zgrabnie zorganizowana siatka kwadratów wypełniająca całe okno:

Każdy z kwadratów składa się z 2 trójkątów o łącznej liczbie 6 wierzchołków. Każdy wierzchołek zawiera wektor położenia 2D w NDC i wektor koloru. Poniżej przedstawiono dane wierzchołków używane w tym przykładzie - trójkąty są dość małe, aby zmieścić tak je na ekranie w tak dużej ilości:
float quadVertices[] = {
// pozycje // kolory
-0.05f, 0.05f, 1.0f, 0.0f, 0.0f,
0.05f, -0.05f, 0.0f, 1.0f, 0.0f,
-0.05f, -0.05f, 0.0f, 0.0f, 1.0f,
-0.05f, 0.05f, 1.0f, 0.0f, 0.0f,
0.05f, -0.05f, 0.0f, 1.0f, 0.0f,
0.05f, 0.05f, 0.0f, 1.0f, 1.0f
};
Kolory kwadratów są kolorowane za pomocą Fragment Shadera, który odbiera wektor koloru z Vertex Shadera:
#version 330 core
out vec4 FragColor;
in vec3 fColor;
void main()
{
FragColor = vec4(fColor, 1.0);
}
Nic nowego jak dotąd, ale w Vertex Shader zaczyna się dziać coś interesującego:
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;
out vec3 fColor;
uniform vec2 offsets[100];
void main()
{
vec2 offset = offsets[gl_InstanceID];
gl_Position = vec4(aPos + offset, 0.0, 1.0);
fColor = aColor;
}
Tutaj zdefiniowaliśmy tablicę uniformów o nazwie offsets, która zawiera łącznie 100 wektorów przesunięcia. Wewnątrz Vertex Shadera pobieramy wektor przesunięcia dla każdej instancji, indeksując tablicę offsets, używając parametru gl_InstanceID. Gdybyśmy narysowali 100 kwadratów za pomocą instancjonowanego wywołania renderowania, otrzymalibyśmy 100 kwadratów znajdujących się w różnych miejscach.
Musimy właściwie ustawić pozycje przesunięcia, które obliczamy w zagnieżdżonej pętli for przed wejściem do pętli gry:
glm::vec2 translations[100];
int index = 0;
float offset = 0.1f;
for(int y = -10; y < 10; y += 2)
{
for(int x = -10; x < 10; x += 2)
{
glm::vec2 translation;
translation.x = (float)x / 10.0f + offset;
translation.y = (float)y / 10.0f + offset;
translations[index++] = translation;
}
}
Tutaj tworzymy zestaw 100 wektorów translacji, które zawierają wektor translacji dla wszystkich pozycji w siatce 10x10. Oprócz generowania tablicy translations musimy również przesłać dane do tablicy uniformów w Vertex Shader:
shader.use();
for(unsigned int i = 0; i < 100; i++)
{
stringstream ss;
string index;
ss << i;
index = ss.str();
shader.setVec2(("offsets[" + index + "]").c_str(), translations[i]);
}
W tym fragmencie kodu przekształcamy licznik pętli for i na
Po zakończeniu wszystkich przygotowań możemy rozpocząć renderowanie kwadratów. Aby narysować za pomocą instancjonowanego wywołania renderowania, wywołujemy
glBindVertexArray(quadVAO);
glDrawArraysInstanced(GL_TRIANGLES, 0, 6, 100);
Parametry 100 kwadratów w siatce 10x10, ustawiamy ją na 100. Uruchomienie kodu powinno dać ci znajomy obraz 100 kolorowych kwadratów.
Tablice instancji
Chociaż poprzednia implementacja działa dobrze w tym konkretnym przypadku użycia, ilekroć renderujemy o wiele więcej niż 100 instancji (co jest dość powszechne), ostatecznie osiągniemy limit o ilości uniformów, które możemy wysłać do shaderów. Inną alternatywą są
W przypadku atrybutów wierzchołków każdy przebieg Vertex Shadera spowoduje, że GLSL pobierze następny zestaw atrybutów wierzchołków należących do bieżącego wierzchołka. Jednak podczas definiowania atrybutu wierzchołków jako tablicy instancji Vertex Shader aktualizuje tylko zawartość atrybutu wierzchołków dla każdej instancji zamiast dla każdego wierzchołka. To pozwala nam używać standardowych atrybutów wierzchołków dla danych wierzchołków i używać tablicy instancji do przechowywania danych, które są unikalne dla każdej instancji.
Aby podać przykład tablicy instancji, weźmiemy poprzedni przykład. Reprezentujemy tablicę uniformów przesunięć jako tablicę instancji. Będziemy musieli zaktualizować Vertex Shader, dodając kolejny atrybut wierzchołków:
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;
layout (location = 2) in vec2 aOffset;
out vec3 fColor;
void main()
{
gl_Position = vec4(aPos + aOffset, 0.0, 1.0);
fColor = aColor;
}
Nie używamy już gl_InstanceID i możemy bezpośrednio używać atrybutu offset bez wcześniejszego indeksowania dużej tablicy uniformów.
Ponieważ tablica instancji jest atrybutem wierzchołkowym, podobnie jak zmienne position i color, musimy również przechowywać jego zawartość w obiekcie bufora wierzchołków i skonfigurować jego wskaźnik atrybutu. Najpierw zapiszemy tablicę translations (z poprzedniej sekcji) do nowego obiektu bufora:
unsigned int instanceVBO;
glGenBuffers(1, &instanceVBO);
glBindBuffer(GL_ARRAY_BUFFER, instanceVBO);
glBufferData(GL_ARRAY_BUFFER, sizeof(glm::vec2) * 100, &translations[0], GL_STATIC_DRAW);
glBindBuffer(GL_ARRAY_BUFFER, 0);
Następnie musimy ustawić jego wskaźnik atrybutu wierzchołka i go włączyć:
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, instanceVBO);
glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 2 * sizeof(float), (void*)0);
glBindBuffer(GL_ARRAY_BUFFER, 0);
glVertexAttribDivisor(2, 1);
To, co czyni ten kod interesującym, to ostatnia linijka, w której wywołujemy funkcję 0, co oznacza, że OpenGL aktualizuje zawartość atrybutu wierzchołka w każdej inwokacji Vertex Shadera. Ustawiając ten atrybut na 1, mówimy OpenGL, że chcemy zaktualizować zawartość atrybutu wierzchołka, gdy zaczniemy renderować nową instancję. Przez ustawienie 2 aktualizujemy zawartość co 2 instancje i tak dalej. Ustawiając dzielnik atrybutów na 1, efektywnie mówimy OpenGL, że atrybut wierzchołka o lokalizacji atrybutu 2 jest tablicą instancji.
Jeśli mamy teraz ponownie renderować kwadraty za pomocą

Jest to dokładnie to samo, co poprzedni przykład, ale tym razem został on wygenerowany za pomocą tablic instancji, co pozwala nam przekazać dużo więcej danych (tyle, ile pozwala na to nam pamięć) do Vertex Shadera dla instancjonowanego renderowania.
Dla zabawy moglibyśmy również powoli zmniejszać skalę każdego kwadratu od prawego górnego rogu aż do dolnego lewego rogu, ponownie używając gl_InstanceID.
void main()
{
vec2 pos = aPos * (gl_InstanceID / 100.0);
gl_Position = vec4(pos + aOffset, 0.0, 1.0);
fColor = aColor;
}
Powoduje to, że pierwsze instancje kwadratów są bardzo małe i im dalej rysujemy instancje, tym bliżej gl_InstanceID jest wartości 100 i tym samym więcej kwadratów odzyskuje swoje pierwotne rozmiary. Używanie tablic instancji razem z gl_InstanceID jest całkowicie legalne.
Jeśli nadal nie masz pewności, jak działa renderowanie instancjonowane lub chcesz zobaczyć, jak wszystko pasuje do siebie, możesz znaleźć pełny kod źródłowy aplikacji tutaj.
Chociaż jest to zabawne i w ogóle, ten przykład nie jest naprawdę dobrym przykładem wykorzystania instancji. Tak, dają one prosty przegląd tego, jak działają instancje, ale ta technika jest niezwykle przydatna przy rysowaniu ogromnej ilości podobnych obiektów, czego tak naprawdę do tej pory nie robiliśmy. Z tego powodu zamierzamy zapuścić się w kosmos w następnej sekcji, aby zobaczyć prawdziwą moc renderowania instancjonowanego.
Pole asteroid
Wyobraźmy sobie scenę, w której mamy jedną wielką planetę, która znajduje się w centrum dużego pierścienia asteroid. Taki pierścień asteroid może zawierać tysiące lub dziesiątki tysięcy formacji skalnych i szybko staje się niemożliwy do renderowania na jakiejkolwiek przyzwoitej karcie graficznej. Ten scenariusz okazuje się szczególnie przydatny do renderowania instancyjnego, ponieważ wszystkie asteroidy można reprezentować za pomocą jednego modelu. Każda pojedyncza asteroida zawiera następnie niewielkie zmiany za pomocą macierzy transformacji, które są unikalne dla każdej asteroidy.
Aby zademonstrować wpływ renderowania instancyjnego, będziemy renderować scenę z asteroidami latającymi wokół planety bez renderowania instancyjnego. Scena będzie zawierała duży model planety, który można pobrać z tutaj oraz duży zestaw asteroidalnych skał, które właściwie ustawiamy wokół planety. Model asteroidy można pobrać tutaj.
W próbkach kodu ładujemy modele za pomocą modułu ładującego, który wcześniej zdefiniowaliśmy w tutorialach o ładowaniu modeli.
Aby uzyskać efekt, którego szukamy, wygenerujemy macierz transformacji dla każdej asteroidy, której użyjemy jako macierzy modelu. Macierz transformacji jest tworzona przez translacje skały gdzieś w pierścieniu asteroidalnym - dodamy także małą wartość losowego przemieszczenia dla tego przesunięcia, aby pierścień wyglądał bardziej naturalnie. Następnie stosujemy losową skalę i losową rotację wokół wektora obrotu. Rezultatem jest macierz transformacji, która przemieszcza każdą asteroidę gdzieś wokół planety, jednocześnie nadając jej bardziej naturalny i niepowtarzalny wygląd w porównaniu do innych asteroid. Rezultatem jest pierścień pełen asteroid, gdzie każda asteroida wygląda inaczej.
unsigned int amount = 1000;
glm::mat4 *modelMatrices;
modelMatrices = new glm::mat4[amount];
srand(glfwGetTime()); // zainicjuj losowe ziarno
float radius = 50.0;
float offset = 2.5f;
for(unsigned int i = 0; i < amount; i++)
{
glm::mat4 model;
// 1. translacja: przesuwaj po okręgu o "promieniu" w zakresie [-offset, offset]
float angle = (float)i / (float)amount * 360.0f;
float displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
float x = sin(angle) * radius + displacement;
displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
float y = displacement * 0.4f; // keep height of field smaller compared to width of x and z
displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
float z = cos(angle) * radius + displacement;
model = glm::translate(model, glm::vec3(x, y, z));
// 2. Skala: przeskaluj od 0.05 do 0.25f
float scale = (rand() % 20) / 100.0f + 0.05;
model = glm::scale(model, glm::vec3(scale));
// 3. rotation: dodaj losową rotację wokół (pół) losowo wybranego wektora osi obrotu
float rotAngle = (rand() % 360);
model = glm::rotate(model, rotAngle, glm::vec3(0.4f, 0.6f, 0.8f));
// 4. teraz dodaj do listy macierzy
modelMatrices[i] = model;
}
Ten fragment kodu może wyglądać trochę zniechęcająco, ale w zasadzie przekształcamy położenie x i z asteroidy wzdłuż okręgu o promieniu określonym przez radius i losowo przemieszczamy każdą asteroidę po okręgu o wartość z zakresu -offset i offset. Dajemy mniejsze przesunięcie y, aby stworzyć bardziej płaski pierścień asteroid. Następnie stosujemy transformacje skalowania i rotacji i przechowujemy wynikową macierz transformacji w modelMatrices, która ma rozmiar amount. Tutaj generujemy w sumie 1000 macierzy modelu, po jednej na asteroidę.
Po załadowaniu modeli planety i skał oraz kompilacji zestawu shaderów kod renderujący wygląda tak:
// narysuj Planet
shader.use();
glm::mat4 model;
model = glm::translate(model, glm::vec3(0.0f, -3.0f, 0.0f));
model = glm::scale(model, glm::vec3(4.0f, 4.0f, 4.0f));
shader.setMat4("model", model);
planet.Draw(shader);
// narysuj meteoryty
for(unsigned int i = 0; i < amount; i++)
{
shader.setMat4("model", modelMatrices[i]);
rock.Draw(shader);
}
Najpierw rysujemy model planety, który przesuwamy i skalujemy, aby dopasować go do sceny, a następnie rysujemy kilka modeli skał o ilości równej wartości amount obliczonych przez nas transformacji. Zanim jednak narysujemy każdy kamień, najpierw ustawiamy odpowiednią macierz transformacji modelu wewnątrz shadera.
Rezultatem jest scena przypominająca kosmos, w której widzimy naturalnie wyglądający pierścień asteroidalny wokół planety:
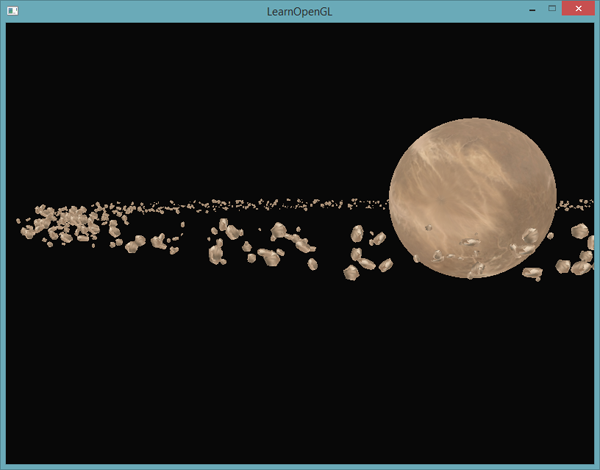
Ta scena zawiera w sumie wywołania renderujące w liczbie 1001 na klatkę, z których 1000 to model asteroidy. Możesz znaleźć kod źródłowy tej sceny tutaj.
Gdy tylko zaczniemy zwiększać tę liczbę, szybko zauważymy, że scena przestaje działać płynnie, a liczba ramek, które możemy renderować na sekundę, drastycznie maleje. Gdy tylko ustawimy amount na 2000 scena renderuje się tak wolno, że trudno jest się poruszać.
Spróbujmy teraz wyrenderować tę samą scenę, ale tym razem za pomocą renderowania instancyjnego. Najpierw musimy zaadaptować do tego Vertex Shader:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in mat4 instanceMatrix;
out vec2 TexCoords;
uniform mat4 projection;
uniform mat4 view;
void main()
{
gl_Position = projection * view * instanceMatrix * vec4(aPos, 1.0);
TexCoords = aTexCoords;
}
Nie używamy już zmiennej modelu, ale zamiast niej deklarujemy 3, kolumny macierzy będą miały położenia atrybutów wierzchołka 3, 4, 5 i 6.
Następnie musimy ustawić każdy z wskaźników tych 4 atrybutów wierzchołków i skonfigurować je jako tablice instancji:
// vertex Buffer Object
unsigned int buffer;
glGenBuffers(1, &buffer);
glBindBuffer(GL_ARRAY_BUFFER, buffer);
glBufferData(GL_ARRAY_BUFFER, amount * sizeof(glm::mat4), &modelMatrices[0], GL_STATIC_DRAW);
for(unsigned int i = 0; i < rock.meshes.size(); i++)
{
unsigned int VAO = rock.meshes[i].VAO;
glBindVertexArray(VAO);
// Atrybuty wierzchołków
GLsizei vec4Size = sizeof(glm::vec4);
glEnableVertexAttribArray(3);
glVertexAttribPointer(3, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)0);
glEnableVertexAttribArray(4);
glVertexAttribPointer(4, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(vec4Size));
glEnableVertexAttribArray(5);
glVertexAttribPointer(5, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(2 * vec4Size));
glEnableVertexAttribArray(6);
glVertexAttribPointer(6, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(3 * vec4Size));
glVertexAttribDivisor(3, 1);
glVertexAttribDivisor(4, 1);
glVertexAttribDivisor(5, 1);
glVertexAttribDivisor(6, 1);
glBindVertexArray(0);
}
Zauważ, że trochę oszukiwaliśmy, deklarując zmienną VAO w klasie
Następnie ponownie bierzemy VAO siatki i tym razem rysujemy ją za pomocą
// rysuj meteoryty
instanceShader.use();
for(unsigned int i = 0; i < rock.meshes.size(); i++)
{
glBindVertexArray(rock.meshes[i].VAO);
glDrawElementsInstanced(
GL_TRIANGLES, rock.meshes[i].indices.size(), GL_UNSIGNED_INT, 0, amount
);
}
W tym przykładzie narysujemy tę samą amount (ilość) asteroid jak we wcześniejszym przykładzie, ale tym razem za pomocą renderowania instancyjnego. Wyniki powinny być podobne, ale zaczniesz naprawdę widzieć efekt renderowania instancyjnego, gdy zaczniemy zwiększać tę zmienną amount. Bez instancji renderowania mogliśmy płynnie renderować od 1000 do 1500 asteroid. Przy renderowaniu instancyjnym możemy teraz ustawić tę wartość na 100000, która z modelem skały mającym 576 wierzchołków jest równa około 57 miliona wierzchołków narysowanych w każdej klatce bez spadku wydajności!

Ten obraz został wyrenderowany z 100000 asteroid o promieniu 150.0f i przesunięciem równym 25.0f. Możesz znaleźć kod źródłowy przykładowego renderowania tutaj.
Na różnych maszynach liczba asteroid na poziomie 100000 może być trochę za duża, więc spróbuj poprawić wartości, aż osiągniesz akceptowalną ilość klatek na sekundę.
Jak widać, w odpowiednim typie środowiska renderowanie instancyjne może ogromnie zmienić możliwości renderowania karty graficznej. Z tego powodu renderowanie instancyjne jest powszechnie używane w przypadku trawy, flory, cząstek i scen podobnych do tego - w zasadzie każda scena z wieloma powtarzającymi się kształtami może odnieść korzyści z renderowania instancyjnego.