This is the Polish translation of PBR/Theory article of learnopengl.com tutorial series.

PBR, lub bardziej powszechnie znany jako rendering oparty na fizyce (ang. physically based rendering) jest zbiorem technik renderowania, które są mniej lub bardziej oparte na tej samej podstawowej teorii, która jest bardziej podobna do tej z fizycznego świata. Ponieważ rendering oparty na fizyce ma na celu naśladować światło w sposób fizycznie wiarygodny, to wygląda on bardziej realistycznie w porównaniu do naszych oryginalnych algorytmów oświetleniowych, takich jak Phong i Blinn-Phong. Nie tylko wygląda lepiej, ponieważ zbliża się do rzeczywistej fizyki, a my (a szczególnie artyści) możemy tworzyć materiały powierzchniowe w oparciu o parametry fizyczne bez konieczności uciekania się do tanich hacków i poprawek, aby oświetlenie wyglądało dobrze. Jedną z większych zalet materiałów autorskich opartych na parametrach fizycznych jest to, że te materiały będą wyglądały poprawnie bez względu na warunki oświetleniowe; nie jest to prawdą w algorytmach innych niż PBR.

Rendering oparty na fizyce jest nadal przybliżeniem rzeczywistości (opartej na zasadach fizyki), dlatego nie nazywa się cieniowaniem fizycznym, ale bazującym na fizyce. Aby model oświetlenia PBR mógł być uważany za bazujący na fizyce, musi spełniać następujące 3 warunki (nie martw się, niedługo je omówimy):

1. Opieraj się na modelu powierzchniowym mikrościanek.
2. Podlega zasadzie zachowania energii.
3. Używa fizycznego modelu funkcji BRDF.

W tej serii tutoriali o PBR skupimy się na podejściu PBR, pierwotnie zbadanym przez Disneya i przyjętym do renderingu w czasie rzeczywistym przez Epic Games. Ich podejście oparte na metalicznym przepływie pracy (ang. metallic workflow) jest przyzwoicie udokumentowane, powszechnie przyjęte w najpopularniejszych silnikach i wygląda niesamowicie. Pod koniec serii będziemy mieli coś, co wygląda tak:

Należy pamiętać, że tematy z tej serii samouczków są raczej zaawansowane, dlatego zaleca się, aby dobrze rozumieć OpenGL i algorytmy oświetlenia/cieniowania. Niektóre z bardziej zaawansowanych tematów, których będziesz potrzebować w tej serii, to: framebuffery, cubemaps, korekcja gamma, HDR, i mapy normalnych. Będziemy również zagłębić się w zaawansowaną matematykę, ale dołożę wszelkich starań, aby wyjaśnić pojęcia tak jasno, jak to tylko możliwe.

Model mikrościanek

Wszystkie techniki PBR oparte są na teorii mikrościanek. Teoria opisuje, że każda powierzchnia w skali mikroskopowej może być opisana przez małe lusterka doskonale odbijające światło, zwane mikrościankami (ang. microfacets). W zależności od szorstkości powierzchni, ułożenie tych drobnych małych lusterek może się bardzo różnić:

Im bardziej szorstka (ang. rough) jest powierzchnia, tym bardziej chaotycznie ułożona jest każda mikrościanka na powierzchni. Efektem tych drobnych zwierciadeł jest to, że gdy mówimy o oświetleniu zwierciadlanym/odbiciu światła, przychodzące promienie światła są bardziej podatne na rozproszenie wzdłuż zupełnie różnych kierunków na szorstkich powierzchniach, co skutkuje bardziej rozprzestrzenionym odbiciem lustrzanym. W przeciwieństwie do tego, na gładkiej (ang. smooth) powierzchni, promienie świetlne z większym prawdopodobieństwem odbijają się, w przybliżeniu, w tym samym kierunku, dając nam mniejsze i ostrzejsze odbicia:

Żadna powierzchnia nie jest całkowicie gładka na poziomie mikroskopowym, ale widząc, że te mikrościanki są na tyle małe, że nie możemy rozróżnić ich na poziomie pikselowym, statystycznie przybliżamy chropowatość mikrościanek na powierzchni za pomocą parametru roughness (ang. chropowatość). W zależności od chropowatości powierzchni możemy obliczyć stosunek mikrościanek z grubsza dopasowanych do wektora $h$ (wektor połowiczny, który znajduje się w połowie odległości między wektorem światła $l$ a wektorem patrzenia $v$). Omówiliśmy już wektor połowiczny w tutorialu zaawansowane oświetlenie, który jest obliczany jako suma $l$ i $v$ podzielona przez jego długość:

\[h = \frac{l + v}{\|l + v\|}\]

Im bardziej mikrościanki są wyrównane do wektora połowicznego, tym ostrzejsze i silniejszy rozbłysk. Wraz z parametrem chropowatości, który waha się między 0 a 1, możemy statystycznie określić wyrównanie mikrościanek:

Widzimy, że wyższe wartości chropowatości wykazują znacznie większy kształt odbicia lustrzanego, w przeciwieństwie do mniejszego i ostrzejszego odbicia lustrzanego gładkich powierzchni.

Zachowanie energii

Aproksymacja mikrościanek wykorzystuje zasadę zachowania energii: energia światła wychodzącego nigdy nie powinna przekraczać przychodzącej energii światła (z wyłączeniem powierzchni emisyjnych). Patrząc na powyższy obraz widzimy wzrost lustrzanego obszaru odbicia, ale również jego jasność maleje wraz ze wzrostem poziomu chropowatości. Gdyby intensywność zwierciadła była taka sama w każdym pikselu, niezależnie od wielkości kształtu zwierciadła, szorstkie powierzchnie emitowałyby znacznie więcej energii, naruszając zasadę zachowania energii. Właśnie dlatego widzimy odbicia zwierciadlane bardziej intensywne na gładkich powierzchniach i słabsze na szorstkich powierzchniach.

Aby utrzymać zasadę zachowania energii, musimy wyraźnie rozróżnić światło rozproszone od zwierciadlanego. W momencie, gdy promień światła trafi na powierzchnię, zostaje podzielony na część refrakcyjną (ang. refraction) i część odbitą (ang. reflection). Część odbita jest światłem, które bezpośrednio odbija się i nie wchodzi w powierzchnię; to jest to, co znamy jako oświetlenie lustrzane. Częścią refrakcyjną jest pozostała część światła, która wchodzi w powierzchnię i zostaje wchłonięta; to jest to, co znamy jako oświetlenie rozproszone.

Jest tu kilka niuansów, ponieważ załamane światło nie jest natychmiast absorbowane przez dotknięcie powierzchni. Z fizyki wiemy, że światło można uznać za wiązkę energii, która porusza się naprzód, dopóki nie straci całej swojej energii; sposób, w jaki wiązka światła traci energię nazywa się kolizją. Każdy materiał składa się z maleńkich cząstek, które mogą kolidować z promieniem świetlnym, jak pokazano poniżej. Cząstki pochłaniają część lub całość energii światła podczas każdej kolizji, która zamienia się w ciepło.

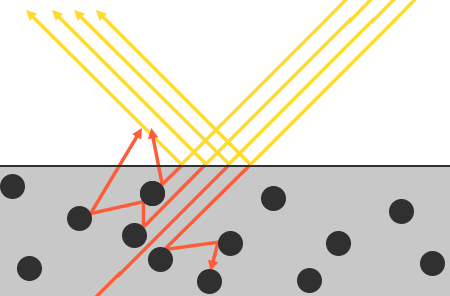
Zasadniczo nie cała energia jest pochłaniana, a światło będzie nadal rozpraszane (ang. scatter) w (w większości) przypadkowych kierunkach, gdzie znowu zderzy się z innymi cząstkami, dopóki jego energia nie zostanie wyczerpana lub ponownie opuści powierzchnię. Promienie światła wychodzące z powierzchni przyczyniają się do zaobserwowanego (rozproszonego) koloru powierzchni. W renderingu opartym na fizyce zakładamy jednak pewne uproszczenie, że całe załamane światło zostaje pochłonięte i rozproszone na bardzo małym obszarze, ignorując efekt rozproszonych promieni świetlnych, które wyszłyby z powierzchni. Konkretne techniki cieniowania, które biorą to pod uwagę, są znane jako techniki podpowierzchniowego rozpraszania (ang. subsurface scattering), które znacznie poprawiają jakość wizualną materiałów takich jak skóra, marmur czy wosk, ale mają one swoją cenę wydajności.

Dodatkową subtelnością, jeśli chodzi o odbicie i załamanie światła, są powierzchnie metaliczne. Powierzchnie metaliczne reagują różnie na światło w porównaniu do powierzchni niemetalicznych (znanych również jako dielektryki). Powierzchnie metalowe podlegają pod te same zasady odbicia i załamania, ale całe załamane światło jest bezpośrednio pochłaniane bez rozpraszania, pozostawiając jedynie rozbłysk lub odbijają światło; powierzchnie metalowe nie wykazują kolorów rozproszenia. Z powodu wyraźnego rozróżnienia, metale i dielektryki traktowane są inaczej w PBR, co omówimy w dalszej części artykułu.

Rozróżnienie światła odbitego i załamanego prowadzi nas do kolejnej obserwacji dotyczącej zachowania energii: wzajemnie się wykluczają. Jakakolwiek energia światła zostanie odbita, nie zostanie już absorbowana przez materiał. Tak więc energia, która została i chce wejść w głąb powierzchni materiału jako światło załamane jest bezpośrednim wynikiem energii po tym, jak uwzględnimy odbicie światła.

Zachowujemy tę relację zachowania energii, najpierw obliczając element odbicia światła, która stanowi procent, jaki przychodzący promień światła oddaje swoją energię. Element światła załamanego jest następnie obliczana bezpośrednio z elementu odbicia jako:

    float kS = calculateSpecularComponent(...); // odbicie światła/komponent specular
    float kD = 1.0 - kS;                        // załamanie światła/komponent diffuse

W ten sposób znamy zarówno ilość światła wchodzącego, która jest odbijana, jak i ilość światła wchodzącego, która jest załamywana, przy jednoczesnym zachowaniu zasady zachowania energii. Biorąc pod uwagę to podejście, nie jest możliwe, aby suma światła załamanego/rozproszonego i odbitego przekroczyła wartość 1.0, zapewniając w ten sposób, że suma ich energii nigdy nie przekracza wejściowej energii światła; coś, czego nie braliśmy pod uwagę w poprzednich tutorialach o oświetleniu.

Równanie odbicia światła

To prowadzi nas do czegoś zwanego równaniem renderowania, które jest dosyć rozbudowanym równaniem, które wymyślili bardzo inteligentni ludzie, który jest obecnie najlepszym modelem do symulowania światła. Rendering oparty na fizyce oparty jest na bardziej wyspecjalizowanej wersji równania renderingu znanego jako równanie odbicia światła (ang. reflectance equation). Aby właściwie zrozumieć PBR, ważne jest, aby najpierw solidnie zrozumieć równanie odbicia:

\[L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]

Równanie odbicia wydaje się początkowo zniechęcające, ale gdy będziemy je powoli analizować to zobaczysz, że powoli zaczyna mieć ono sens. Aby zrozumieć równanie, musimy zagłębić się w teorii radiometrii. Radiometria to pomiar promieniowania elektromagnetycznego (w tym światła widzialnego). Istnieje kilka radiometrycznych wielkości, które możemy wykorzystać do pomiaru światła, ale omówimy tylko jedną, która jest odpowiednia dla równania odbicia zwana jako radiancja (ang. radiance), oznaczonego tutaj jako $L$. Radiancja służy do kwantyfikacji wielkości lub siły światła pochodzącego z jednego kierunku. Z początku trochę trudno to zrozumieć, ponieważ radiancja jest kombinacją wielu fizycznych wielkości, więc skupimy się na tych pierwszych:

Strumień promieniowania: oznaczony jako $\Phi$ jest przesyłaną energią źródła światła mierzoną w watach. Światło jest zbiorczą sumą energii o wielu różnych długościach fal, przy czym każda długość fali jest powiązana z określonym (widzialnym) kolorem. Emitowana energia źródła światła może być zatem uważana za funkcję wszystkich jej różnych długości fal. Długości fal od 390 nm do 700 nm (nanometry) są uważane za część widma światła widzialnego, tj. długości fal, które ludzkie oko jest w stanie odbierać. Poniżej znajduje się obraz różnych energii na długość fali światła dziennego:

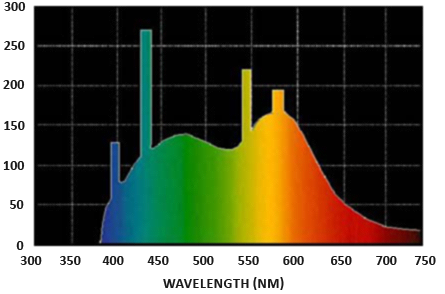
Strumień promieniowania mierzy całkowity obszar tej funkcji o różnych długościach fal. Bezpośrednie przyjmowanie tej długości fal jako danych wejściowych w grafice komputerowej jest nieco niepraktyczne, dlatego często upraszczamy przedstawianie strumienia promieniowania nie jako funkcji o różnej mocy fal, ale jako trójkolorowy kolor światła zakodowany jako RGB (lub jak powszechnie to nazywają: kolor światła). Przez kodowanie tracimy dużą część informacji, ale w przypadku aspektów wizualnych jest to zazwyczaj nieistotne.

Kąt bryłowy: oznaczony jako $\omega$ mówi nam o wielkości lub obszarze kształtu rzutowanego na jednostkową sferę. Obszar rzutowanego kształtu na tę jednostkową sferę jest znany jako kąt bryłowy; możesz zwizualizować kąt bryłowy jako kierunek z objętością:

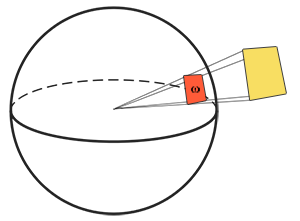
Pomyśl o byciu obserwatorem w centrum tej jednostkowej sfery i patrzysz w kierunku tego kształtu; rozmiar zarysu, który zrobisz z tego kształtu jest kątem bryłowym.

Natężenie promieniowania: intensywność promieniowania mierzy ilość strumienia promieniowania na kąt bryłowy lub inaczej: siłę źródła światła nad rzutowanym obszarem na jednostkowej sferze. Na przykład, biorąc pod uwagę punktowe źródło światła, które promieniuje jednakowo we wszystkich kierunkach, natężenie promieniowania może dać nam swoją energię na określonym obszarze (kąt bryłowy):

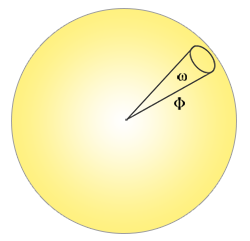
Równanie opisujące intensywność promieniowania definiuje się następująco:

\[I = \frac{d\Phi}{d\omega}\]

Gdzie $I$ to strumień promieniowania $\Phi$ podzielony przez kąt bryłowy $\omega$.

Znając pojęcia strumienia promieniowania, intensywności promieniowania i kąta bryłowego, możemy ostatecznie opisać równanie radiancji, które jest opisane jako całkowita obserwowana energia na obszarze $A$ na kąt bryłowy $\omega$ światła o intensywności promieniowania $\Phi$:

\[L=\frac{d^2\Phi}{ dA d\omega \cos\theta}\]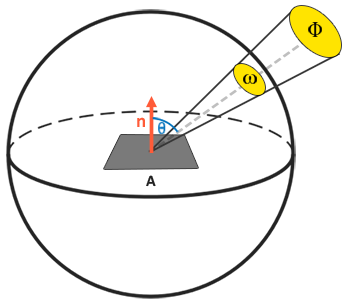

Radiancja jest radiometryczną miarą ilości światła na powierzchni skalowanej przez przychodzący (ang. incident) kąt $\theta$ światła do względem wektora normalnego powierzchni jako $\cos\theta$: światło jest słabsze im mniej promieniuje bezpośrednio na powierzchnię i jest najsilniejsze, gdy jest bezpośrednio prostopadłe do ​​powierzchni. Jest to podobne do naszego rozumienia oświetlenia rozproszonego z serii tutoriali o podstawach oświetlenia, ponieważ $\cos\theta$ bezpośrednio odpowiada iloczynowi skalarnemu między wektorem kierunku światła i wektora normalnego powierzchni:

    float cosTheta = dot(lightDir, N);  

Równanie radiancji jest całkiem użyteczne, ponieważ składa się w większości z fizycznych wielkości, którymi jesteśmy zainteresowani. Jeśli uznamy, że kąt bryłowy $\omega$ i obszar $A$ są nieskończenie małe, możemy użyć radiancji do zmierzenia strumienia promieniowania pojedynczego promienia światła trafiającego w pojedynczy punkt w przestrzeni. Ta zależność pozwala nam obliczyć promieniowanie pojedynczego promienia światła oddziałującego na pojedynczy punkt (fragment); zmieniamy nazewnictwo kąta bryłowego $\omega$ na wektor kierunku $\omega$, a $A$ na punkt $p$. W ten sposób możemy bezpośrednio wykorzystywać radiancję w naszych shaderach do obliczania kontrybucji pojedynczego promienia światła dla fragmentu.

W rzeczywistości, jeśli chodzi o radiancję, ogólnie dbamy o całe padające światło na punkt $p$, który jest sumą wszystkich radiancji, co jest znane jako irradiancja (natężenie promieniowania). Dzięki znajomości zarówno radiancji, jak i natężenia promieniowania możemy wrócić do równania odbicia:

\[L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]

Teraz wiemy, że $L$ w równaniu renderowania reprezentuje radiancję jakiegoś punktu $p$ i jakiegoś nadchodzącego, nieskończenie małego kąta bryłowego $\omega_i$, który można uważać za wektor kierunku $\omega_i$. Pamiętaj, że $\cos\theta$ skaluje energię w oparciu o kąt padania światła na powierzchnię, którą odnajdujemy w równaniu odbicia jako $n \cdot\omega_i$. Równanie odbicia oblicza sumę odbijanego promieniowania $L_o (p, \omega_o)$ punktu $p$ w kierunku $\omega_o$, który jest wychodzącym kierunkiem do kamery. Lub inaczej: $L_o$ mierzy odbitą sumę irradiancji świateł na punkt $p$ oglądany z $\omega_o$.

Ponieważ równanie odbicia jest oparte na natężeniu promieniowania, które jest sumą wszystkich napływających promieni, mierzymy światło nie tylko w jednym kierunku światła, ale we wszystkich kierunkach światła padającego w obrębie półkuli $\Omega$ wokół punktu $p$. Półkulę (ang. hemisphere) można opisać jako połówkę kuli wyrównaną do wektora normalnego powierzchni $n$:

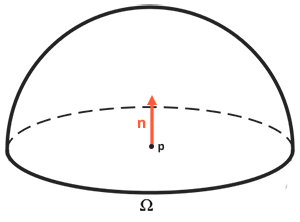
Aby obliczyć sumę wartości wewnątrz obszaru lub, w przypadku półkuli, objętość, używamy konstrukcji matematycznej zwanej całką oznaczoną w równaniu odbicia jako $\int$ we wszystkich nadchodzących kierunkach $d\omega_i$ w obrębie półkuli $\Omega$. Całka mierzy powierzchnię pod wykresem funkcji, który można obliczyć analitycznie lub numerycznie. Ponieważ nie ma analitycznego rozwiązania zarówno dla równania renderowania, jak i równania odbicia, będziemy chcieli numerycznie rozwiązać całkę. Przekłada się to na przyjmowanie wyniku małych dyskretnych kroków równania odbicia na półkuli $\Omega$ i uśrednianie ich wyników w stosunku do wielkości kroku. Jest to znane jako suma Riemanna, którą możemy z grubsza zwizualizować w kodzie w następujący sposób:

    int steps = 100;
    float sum = 0.0f;
    vec3 P    = ...;
    vec3 Wo   = ...;
    vec3 N    = ...;
    float dW  = 1.0f / steps;
    for(int i = 0; i < steps; ++i) 
    {
        vec3 Wi = getNextIncomingLightDir(i);
        sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW;
    }

Przez skalowanie kroków przez dW suma będzie równa całkowitej powierzchni lub objętości funkcji całkowej. dW do skalowania każdego dyskretnego kroku można uważać za $d\omega_i$ w równaniu odbicia. Matematycznie $d\omega_i$ jest symbolem ciągłym, po którym obliczamy całkę i chociaż nie odnosi się bezpośrednio do dW w kodzie (ponieważ jest to dyskretny krok sumy Riemanna), pomaga myśleć w ten sposób. Pamiętaj, że podejmowanie dyskretnych kroków zawsze da nam przybliżenie całkowitego obszaru funkcji. Uważny czytelnik zauważy, że możemy zwiększyć dokładność sumy Riemanna, zwiększając liczbę kroków.

Równanie odbicia sumuje radiancję ze wszystkich nadchodzących kierunków światła $\omega_i$ na półkuli $\omega_i$ skalowaną przez $f_r$, które uderzyły punkt $p$ i zwraca sumę odbitego światła $L_o$ w kierunku widza. Przychodząca radiancja może pochodzić ze źródeł światła, tak jak jesteśmy zaznajomieni lub z mapy otoczenia mierzącej radiancję z każdego nadchodzącego kierunku, co omówimy w tutorialu o IBL (ang. Image Based Lighting).

Teraz jedyną niewiadomą jaka nam została jest $f_r$ znany jako BRDF lub dwukierunkowa funkcja rozkładu odbicia (ang. bidirectional reflective distribution function), która skaluje lub waży nadchodzącą radiancję w oparciu o właściwości materiału powierzchni.

BRDF

BRDF lub dwukierunkowa funkcja rozkładu odbicia (ang. bidirectional reflective distribution function) jest funkcją, która przyjmuje jako wejście kierunek światła $\omega_i$, kierunek patrzenia $\omega_o$, wektor normalny powierzchni $n$ oraz parametr powierzchni $a$, który reprezentuje chropowatość mikropowierzchni. BRDF przybliża, w jakim stopniu każdy poszczególny promień światła $\omega$ przyczynia się do końcowego odbitego światła nieprzezroczystej powierzchni, biorąc pod uwagę jego właściwości materiałowe. Na przykład, jeśli powierzchnia ma idealnie gładką powierzchnię (jak ​​lustro), funkcja BRDF zwróci 0.0 dla wszystkich przychodzących promieni światła $\omega_i$ z wyjątkiem jednego promienia, który ma ten sam kąt (odbicia) jak wychodzący promień $\omega_o$, dla którego funkcja zwraca 1.0.

BRDF przybliża właściwości odbijające i refrakcyjne materiału w oparciu o wcześniej omawianą teorię mikrościanek. Aby BRDF był oparty na fizyce, musi przestrzegać prawa zachowania energii, tj. suma odbitego światła nigdy nie powinna przekraczać ilości światła przychodzącego. Technicznie rzecz biorąc, Blinn-Phong jest uważany za BRDF przy tych samych danych wejściowych $\omega_i$ i $\omega_o$. Jednak Blinn-Phong nie jest uważany za fizycznie poprawny, ponieważ nie przestrzega zasady zachowania energii. Istnieje kilka fizycznych BRDF, które pozwalają na przybliżenie reakcji powierzchni ze światłem. Jednak prawie wszystkie potoki renderowania w czasie rzeczywistym używają BRDF znanego jako Cook-Torrance BRDF.

BRDF Cook-Torrance zawiera zarówno część rozproszoną (diffuse), jak i lustrzaną (specular):

\[f_r = k_d f_{lambert} + k_s f_{cook-torrance}\]

Tutaj $k_d$ jest wspomnianym wcześniej współczynnikiem przychodzącej energii światła, która zostaje załamana, gdzie $k_s$ jest współczynnikiem, który określa ilość załamanego światła. Lewa strona BRDF wskazuje rozproszoną część równania, oznaczoną tutaj jako $f_{lambert}$. Jest to znane jako rozproszenie Lamberta (ang. Lambertian diffuse) podobne do tego, którego używaliśmy do cieniowania diffuse, która jest stałą oznaczoną jako:

\[f_{lambert} = \frac{c}{\pi}\]

Gdzie $c$ określa albedo/kolor powierzchni (pomyśl o teksturze diffuse powierzchni). Dzielenie przez pi ma na celu znormalizowanie rozproszonego światła, ponieważ wcześniej oznaczona całka zawierająca BRDF jest skalowana przez $\pi$ (dojdziemy do tego samouczku o IBL).

Możesz się zastanawiać, w jaki sposób to rozproszenie Lamberta wiąże się z terminem diffuse, którego używaliśmy wcześniej: kolor powierzchni pomnożony przez iloczyn skalarny pomiędzy wektorem normalnym i kierunkiem światła. Iloczyn skalarny wciąż tam jest, ale został usunięty z BRDF i możemy $n \cdot \omega_i$ na końcu całki $L_o$.

Istnieją różne równania dla rozproszonej części BRDF, które wydają się bardziej realistyczne, ale są również bardziej kosztowne obliczeniowo. Jednakże, jak stwierdził Epic Games, rozproszenie Lamberta jest wystarczające dla większości przypadków renderowania w czasie rzeczywistym.

Lustrzana część BRDF jest nieco bardziej zaawansowana i jest opisana jako:

\[f_{cook-torrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}\]

Specular Cook-Torrance BRDF składa się z trzech funkcji i współczynnika normalizacji w mianowniku. Każdy z symboli D, F i G reprezentuje typ funkcji, która przybliża (aproksymuje) określoną części właściwości odbijających powierzchni. Są one zdefiniowane jako funkcja rozkładu wektorów normalnych (ang. normal Distribution function), równanie Fresnel’a (ang. Fresnel equation) i funkcja Geometrii (ang. Geometry function):

• Normal distribution function: przybliża to w jaki sposób mikrościanki na powierzchni są wyrównane do wektora połowicznego (ang. halfway vector), na który wpływa chropowatość powierzchni; jest to podstawowa funkcja przybliżania mikrościanek.
• Geometry function: opisuje właściwość samo-zacieniania mikrościanek. Kiedy powierzchnia jest stosunkowo szorstka, mikrościanki powierzchni mogą rzucać cień na inne mikrościanki, zmniejszając w ten sposób światło, które jest odbijane przez powierzchnię.
• Fresnel equation: Równanie Fresnel’a opisuje współczynnik odbicia powierzchni przy różnych kątach.

Każda z tych funkcji jest przybliżeniem ich odpowiedników z fizyki i znajdziesz więcej niż jedną wersję każdego z tych równań, które mają na celu przybliżenie fizcznych równań; niektóre są bardziej realistyczne, inne bardziej wydajne. Dozwolone jest wybranie dowolnej wersji tych funkcji, których chcesz użyć. Brian Karis z Epic Games przeprowadził wiele badań nad różnymi typami aproksymacji tutaj. Wybieramy te same funkcje, które są używane przez Unreal Engine 4 Epic Games, czyli Trowbridge-Reitz GGX dla D, przybliżenie Fresnela-Schlicka dla F i Smitha-Schlicka-GGX dla G.

Normal distribution function

Funkcja dystrybucji wektorów normalnych $D$ statystycznie przybliża względną powierzchnię mikrościanek dokładnie wyrównanych do wektora (połowicznego) $h$. Istnieje wiele zdefiniowanych funkcji NDF, które statystycznie przybliżają ogólne wyrównanie mikrościanek przy danym parametrze chropowatości, a ta, której będziemy używać, jest znana jako funkcja Trowbridge-Reitz GGX:

\[NDF_{GGX TR}(n, h, \alpha) = \frac{\alpha^2}{\pi((n \cdot h)^2 (\alpha^2 - 1) + 1)^2}\]

Tutaj $h$ jest wektorem połowicznym do porównania z mikrościanką powierzchni, przy czym $a$ jest miarą chropowatości powierzchni. Jeśli weźmiemy $h$ jako wektor w połowie drogi między wektorem normalnym powierzchni i kierunkiem światła przy różnych parametrach chropowatości, otrzymamy następujący efekt wizualny:

Kiedy chropowatość jest niska (a więc powierzchnia jest gładka), wysoko skoncentrowana liczba mikrościanek jest dopasowywana do wektorów połowicznych w małym promieniu. Ze względu na to wysokie zagęszczenie NDF wyświetla bardzo jasny punkt. Jednak na chropowatej powierzchni, gdzie mikrościanki są ustawione w znacznie bardziej losowych kierunkach, znajdziesz znacznie większą liczbę wektorów połowicznych $h$ wyrównanych do mikrościanek, ale mniej zagęszczonych co daje nam bardziej szare wyniki.

W kodzie GLSL funkcja rozkładu wektorów normalnych Trowbridge-Reitz GGX wyglądałaby mniej więcej tak:

    float DistributionGGX(vec3 N, vec3 H, float a)
    {
        float a2     = a*a;
        float NdotH  = max(dot(N, H), 0.0);
        float NdotH2 = NdotH*NdotH;

        float nom    = a2;
        float denom  = (NdotH2 * (a2 - 1.0) + 1.0);
        denom        = PI * denom * denom;

        return nom / denom;
    }

Geometry function

Funkcja geometrii jest statystycznie przybliża względne pole powierzchni, gdzie mikrościanki przesłaniają się nawzajem, powodując zasłonięcie promieni świetlnych.

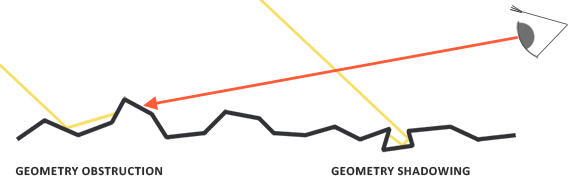
Podobnie jak w przypadku NDF, funkcja Geometrii przyjmuje parametr chropowatości materiału jako dane wejściowe, gdzie bardziej szorstkie powierzchnie mają większe prawdopodobieństwo zacieniania mikrościanek. Funkcja geometrii, której użyjemy, jest połączeniem aproksymacji GGX i Schlick-Beckmann’a znanego jako Schlick-GGX:

\[G_{SchlickGGX}(n, v, k) = \frac{n \cdot v} {(n \cdot v)(1 - k) + k }\]

Tutaj $k$ jest mapowaniem $\alpha$ w oparciu o to, czy używamy funkcji geometrii dla oświetlenia bezpośredniego, czy IBL:

\[k_{direct} = \frac{(\alpha + 1)^2}{8}\] \[k_{IBL} = \frac{\alpha^2}{2}\]

Zauważ, że wartość $\alpha$ może się różnić w zależności od tego, jak twój silnik mapuje chropowatość na $\alpha$. W poniższych samouczkach obszernie omówimy, jak i gdzie to ponowne mapowanie staje się istotne.

Aby skutecznie przybliżyć geometrię, musimy wziąć pod uwagę zarówno kierunek patrzenia (zasłonięcie geometrii), jak i wektor kierunku światła (cienie geometrii). Możemy wziąć obie rzeczy pod uwagę używając metody Smith'a:

\[G(n, v, l, k) = G_{sub}(n, v, k) G_{sub}(n, l, k)\]

Użycie metody Smitha z Schlick-GGX jako $G_{sub}$ daje następujący efekt wizualny ze zmienną szorstkością R:

Funkcja geometrii jest mnożnikiem pomiędzy [0.0, 1.0], gdzie 1.0 oznacza brak rzucania cieni przez mikrościanki i 0.0 oznaczającym kompletne zacienienie mikrościanki.

W GLSL funkcja geometrii przekłada się na następujący kod:

    float GeometrySchlickGGX(float NdotV, float k)
    {
        float nom   = NdotV;
        float denom = NdotV * (1.0 - k) + k;

        return nom / denom;
    }

    float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
    {
        float NdotV = max(dot(N, V), 0.0);
        float NdotL = max(dot(N, L), 0.0);
        float ggx1 = GeometrySchlickGGX(NdotV, k);
        float ggx2 = GeometrySchlickGGX(NdotL, k);

        return ggx1 * ggx2;
    }

Fresnel equation

Równanie Fresnela (wymawiane jako Freh-nel) opisuje stosunek światła, które jest odbijane do światła, które ulega załamaniu, które zmienia się w zależności od tego pod jakim kątem patrzymy na powierzchnię. Moment uderzenia światła w powierzchnię, w oparciu o kąt wektora patrzenia do powierzchni, równanie Fresnela mówi nam o procentowym odbiciu światła. Z tego stosunku odbicia i zasady zachowania energii możemy bezpośrednio uzyskać załamaną część światła z jego pozostałej energii.

Każda powierzchnia lub materiał ma poziom podstawowego współczynnika odbicia (ang. base reflectivity) podczas patrzenia prosto na jego powierzchnię, ale podczas patrzenia na powierzchnię pod kątem wszystkie odbicia stają się bardziej widoczne w porównaniu do podstawowego współczynnika odbicia powierzchni. Możesz to sprawdzić samodzielnie, patrząc na swoje prawdopodobnie drewniane/metalowe biurko o pewnym współczynniku odbicia z prostopadłego kierunku patrzenia, ale patrząc na biurko pod kątem prawie 90 stopni zobaczysz, że odbicia stają się znacznie bardziej widoczne. Wszystkie powierzchnie teoretycznie w pełni odbijają światło, jeśli widzimy je pod idealnym kątem 90 stopni. Zjawisko to znane jest jako Fresnel i jest opisane równaniem Fresnela.

Równanie Fresnela jest dość złożonym równaniem, ale na szczęście można je przybliżać za pomocą aproksymacji Fresnel-Schlick'a:

\[F_{Schlick}(h, v, F_0) = F_0 + (1 - F_0) ( 1 - (h \cdot v))^5\]

$F_0$ reprezentuje podstawowy współczynnik odbicia powierzchni, który obliczamy za pomocą tak zwanych współczynników refrakcji (ang. indices of refraction) lub IOR i jak widać na powierzchni sfery, im bardziej patrzymy w kierunku kątów prostopadłych do powierzchni tym silniejszy jest efekt Fresnela, a tym samym odbicia:

Istnieje kilka subtelności związanych z równaniem Fresnela. Po pierwsze, przybliżenie Fresnela-Schlicka jest zdefiniowane tylko dla dielektryków lub powierzchni niemetalowych. Dla przewodników (metale) obliczając podstawowy współczynnik odbicia za pomocą ich współczynników refrakcji to nie zachowują się one poprawnie i musimy użyć innego równania Fresnela dla przewodników. Ponieważ jest to niewygodne, dodatkowo aproksymujemy tę funkcję przez wstępne obliczenie $F_0$ (pod kątem 0 stopni, tak jakbyśmy patrzyli bezpośrednio na powierzchnię) i interpolujemy te wartości w oparciu o kąt patrzenia, tak że możemy użyć tego samego równania dla metali i niemetali.

Podstawowe współczynniki odbicia powierzchni można znaleźć w dużych bazach danych, takich jak ta, z niektórymi bardziej powszechnymi wartościami wymienionymi poniżej, zaczerpniętymi z notatek kursu Naty’ego Hoffmana:

Materiał	$F_0$ (Liniowy)	$F_0$ (sRGB)	Kolor
Woda	(0.02, 0.02, 0.02)	(0.15, 0.15, 0.15)
Plastik / Szkło (niski)	(0.03, 0.03, 0.03)	(0.21, 0.21, 0.21)
Plastik (wysoki)	(0.05, 0.05, 0.05)	(0.24, 0.24, 0.24)
Szkło (wysoki) / Rubin	(0.08, 0.08, 0.08)	(0.31, 0.31, 0.31)
Diament	(0.17, 0.17, 0.17)	(0.45, 0.45, 0.45)
Żelazo	(0.56, 0.57, 0.58)	(0.77, 0.78, 0.78)
Miedź	(0.95, 0.64, 0.54)	(0.98, 0.82, 0.76)
Złoto	(1.00, 0.71, 0.29)	(1.00, 0.86, 0.57)
Aluminium	(0.91, 0.92, 0.92)	(0.96, 0.96, 0.97)
Srebro	(0.95, 0.93, 0.88)	(0.98, 0.97, 0.95)

Interesujące jest to, że dla wszystkich powierzchni dielektrycznych współczynnik odbicia podstawowego nigdy nie jest wyższy niż 0.17, co jest raczej wyjątkiem niż regułą, podczas gdy dla przewodników współczynnik odbicia podstawowego zaczyna się znacznie wyżej i (w większości) waha się między 0.5 a 1.0. Ponadto, dla przewodników lub powierzchni metalicznych współczynnik odbicia podstawowego jest zabarwiony, dlatego też $F_0$ prezentowane jest jako trójka RGB (współczynnik odbicia przy normalnej częstotliwości może się różnić w zależności od długości fali); to jest coś, co tylko widzimy na metalicznych powierzchniach.

Te specyficzne cechy powierzchni metalicznych w porównaniu z powierzchniami dielektrycznymi spowodowały coś, co nazwano metalicznym przepływem pracy (ang. metallic workflow), w którym wprowadzamy dodatkowy parametr znany jako metalness, który opisuje czy powierzchnia jest powierzchnią metaliczną czy niemetaliczną.

Teoretycznie metaliczność powierzchni jest binarna: jest albo metalem, albo nie; to nie może być jedno i drugie. Jednak większość potoków renderowania umożliwia konfigurację metaliczności powierzchni ustawianą liniowo między 0.0 a 1.0. Wynika to głównie z braku precyzji tekstury materiału, aby opisać na przykład powierzchnię mającą małe cząstki/rysy kurzu/piasku na metalicznej powierzchni. Poprzez zbilansowanie wartości metaliczności wokół tych małych niemetalicznych cząstek/zadrapań otrzymujemy wizualnie przyjemne wyniki.

Poprzez wstępne obliczenie $F_0$ dla dielektryków i przewodników możemy użyć tego samego przybliżenia Fresnela-Schlicka dla obu typów powierzchni, ale musimy ustawić współczynnik odbicia podstawowego, jeśli mamy metaliczną powierzchnię. Zwykle osiągamy to w następujący sposób:

    vec3 F0 = vec3(0.04);
    F0      = mix(F0, surfaceColor.rgb, metalness);

Definiujemy podstawowy współczynnik odbicia, który jest przybliżony dla większości powierzchni dielektrycznych. Jest to kolejna aproksymacja, ponieważ $F_0$ jest uśredniane dla najbardziej powszechnych dielektryków. Podstawowy współczynnik odbicia wynoszący 0.04 stosuje się dla większości dielektryków i daje fizycznie wiarygodne wyniki bez konieczności tworzenia dodatkowego parametru powierzchni. Następnie, bazując na tym, jak metaliczna jest powierzchnia, odbieramy współczynnik odbicia od dielektryka lub przyjmujemy kolor $F_0$ jako kolor powierzchni. Ponieważ metalowe powierzchnie pochłaniają całe załamane światło, nie mają one rozproszonych odbić i możemy bezpośrednio użyć tekstury koloru powierzchni jako ich współczynnika odbicia podstawowego.

W kodzie przybliżenie Fresnela Schlicka przekłada się na:

    vec3 fresnelSchlick(float cosTheta, vec3 F0)
    {
        return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
    }

Gdzie cosTheta jest wynikiem iloczynu skalarnego między wektorem normalnym powierzchni $n$ a kierunkiem patrzenia $v$.

Równanie odbicia Cook-Torrance’a

Z każdym komponentem opisanym przez BRDF Cook-Torrance możemy włączyć fizyczny BRDF do końcowego równania odbicia:

\[L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]

To równanie nie jest jednak w pełni matematycznie poprawne. Być może pamiętasz, że wyrażenie Fresnela $F$ reprezentuje stosunek światła, które jest odbijane na powierzchni. Jest to efektywnie nasz stosunek $k_s$, co oznacza, że ​​część lustrzana równań lustrzanych domyślnie zawiera współczynnik odbicia $k_s$. Biorąc to pod uwagę, nasze końcowe równanie odbicia staje się:

\[L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]

Równanie teraz całkowicie opisuje fizycznie oparty model renderowania, który jest powszechnie uznawany za to, co powszechnie rozumiemy jako rendering fizyczny lub PBR. Nie martw się, jeśli jeszcze nie do końca rozumiesz, w jaki sposób będziemy musieli dopasować całą omawianą matematykę do kodu. W kolejnych samouczkach omówimy, w jaki sposób wykorzystać równanie odbicia, aby uzyskać znacznie bardziej wiarygodne wyniki w naszym renderowanym oświetleniu, a wszystkie elementy powinny powoli dopasowywać się do siebie.

Tworzenie materiałów PBR

Wiedząc o podstawowym modelu matematycznym PBR, sfinalizujemy dyskusję, opisując, w jaki sposób artyści na ogół tworzą fizyczne właściwości powierzchni, którą możemy bezpośrednio wprowadzić do równań PBR. Każdy z parametrów powierzchni, których potrzebujemy do potoku PBR, można zdefiniować lub modelować za pomocą tekstur. Używanie tekstur daje nam kontrolę per-fragment nad tym, jak każdy konkretny punkt powierzchni powinien reagować na światło: czy ten punkt jest metaliczny, szorstki lub gładki, czy też powierzchnia reaguje na różne długości fali światła.

Poniżej znajduje się lista tekstur, które często znajdują się w potoku PBR wraz z jego wizualnym wynikiem, jeśli są dostarczane do renderera PBR:

Albedo: tekstura albedo określa dla każdego teksela kolor powierzchni lub współczynnik odbicia podstawowego, jeśli ten teksel jest metaliczny. Jest to w dużej mierze podobne do tego, co wcześniej używaliśmy jako tekstury rozproszonej, ale wszystkie informacje o oświetleniu są pobierane z tekstury. Rozproszone tekstury często mają nieznaczne cienie lub zaciemnione szczeliny wewnątrz obrazu, czego nie chcemy w teksturach albedo; powinna zawierać tylko kolor (lub załamane współczynniki absorpcji) powierzchni.

Normal: tekstura mapy normalnych jest dokładnie taka sama jak poprzednio w samouczku Mapy normalnych. Mapy normalnych pozwalaja nam określić dla każdego fragmentu unikalny wektor normalny, aby dać iluzję, że powierzchnia jest bardziej wyboista niż jej płaski odpowiednik.

Metallic: mapa metaliczności określa per teksel, czy jest metaliczny, czy nie. Na podstawie tego, jak skonfigurowany jest silnik PBR, artyści mogą tworzyć mapy metaliczności jako wartości w skali szarości lub jako binarną czerń lub biel.

Roughness: mapa szorstkości określa, jak szorstka jest powierzchnia na podstawie teksela. Próbkowana wartość chropowatości mapy chropowatości wpływa na orientację mikrościanek na powierzchni. Chropowata powierzchnia staje się szersza i bardziej rozmyta, a gładka powierzchnia skupia światło i wyraźnie je odbija. Niektóre silniki PBR oczekują mapy smoothness zamiast mapy szorstkości, którą niektórzy artyści uważają za bardziej intuicyjną, ale wartości te zostają przekształcone (1.0 - smoothness) w mapę szorstkości w chwili, gdy są próbkowane.

AO: Mapa ambient occlusion lub AO określa dodatkowy współczynnik cieniowania powierzchni i potencjalnie otaczającej geometrii. Jeśli mamy na przykład ceglaną powierzchnię, tekstura albedo nie powinna zawierać żadnych informacji o cieniach wewnątrz szczelin cegły. Mapa AO określa jednak te przyciemnione krawędzie, ponieważ mniej światła dociera w te szczeliny. Uwzględnienie ambient occlusion na końcu etapu oświetlenia może znacznie poprawić jakość wizualną sceny. Mapa ambient occlusion siatki/powierzchni jest albo ręcznie generowana, albo wstępnie obliczana w programach do modelowania 3D.

Artyści ustawiają i dostosowują te fizyczne wartości wejściowe per teksel i mogą opierać swoje wartości tekstury na fizycznych właściwościach powierzchni materiałów rzeczywistych. Jest to jedna z największych zalet potoku renderowania PBR, ponieważ te fizyczne właściwości powierzchni pozostają takie same, niezależnie od ustawień środowiska i oświetlenia, co ułatwia artystom uzyskanie wiarygodnych wyników. Powierzchnie utworzone w potoku PBR mogą z łatwością być współdzielone między różnymi silnikami PBR. Będą wyglądały poprawnie, niezależnie od środowiska, w którym się znajdują, a co za tym idzie wyglądają bardziej naturalnie.

Więcej informacji

• Tło: Fizyka i matematyka cieniowania autorstwa Naty’ego Hoffmanna: jest zbyt dużo teorii do pełnego jej omówienia w jednym artykule, więc teoria przedstawiona w tym tutorialu to bardzo krótki wstęp; jeśli chcesz dowiedzieć się więcej o fizyce światła i jego związku z teorią PBR to jest to zasób, który chcesz przeczytać.
• Real shading in Unreal Engine 4: omawia model PBR przyjęty przez Epic Games w ich czwartej wersji Unreal Engine. System PBR, na którym skoncentrujemy się w tych samouczkach, oparty jest na tym modelu PBR.
• Marmoset: PBR Theory: wprowadzenie do PBR w większości przeznaczone dla artystów, ale mimo to jest to dobra lektura.
• Coding Labs: Physically based rendering: wprowadzenie do równania renderowania i jego związku z PBR.
• Coding Labs: Physically Based Rendering - Cook–Torrance: wprowadzenie do BRDF Cook-Torrance.
• Wolfire Games - Physically based rendering: wprowadzenie do PBR przez Lukasa Orsvärna.
• [SH17C] Physically Based Shading: świetny interaktywny przykład shadertoy (uwaga: może zająć trochę czasu, aby się załadował) autorstwa Krzysztofa Narkowi pokazujący interakcję światła z materiałem w stylu PBR.