This is the Polish translation of PBR/Lighting article of learnopengl.com tutorial series.
W poprzednim tutorialu omówiliśmy podstawy renderingu opartego na fizyce. W tym samouczku skupimy się na dodaniu omówionej wcześniej teorii do rzeczywistego renderera, który wykorzystuje bezpośrednie (lub analityczne) źródła światła: mowa o światłach punktowych, światłach kierunkowych i/lub reflektorowych.
Zacznijmy od przypomnienia końcowego równania odbicia z poprzedniego samouczka:
\[L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]Teraz wiemy już co się mniej więcej dzieje, ale wciąż pozostaje nieznane, jak dokładnie będziemy reprezentować natężenie promieniowania, całkowitą radiancję $L$ sceny, itp. Wiemy, że radiancja $L$ (zgodnie z interpretacją grafiki komputerowej) mierzy strumień promieniowania $\phi$ lub energię światła źródła światła o danym kącie bryłowym $\omega$. W naszym przypadku przyjęliśmy, że kąt bryłowy $\omega$ jest nieskończenie mały, w takim przypadku radiancja mierzy strumień źródła światła dla pojedynczego promienia światła lub wektora kierunkowego.
Biorąc pod uwagę tę wiedzę, to w jaki sposób możemy to odnieść do części wiedzy na temat oświetlenia, którą zgromadziliśmy na podstawie poprzednich samouczków? Wyobraźmy sobie, że mamy pojedyncze światło punktowe (źródło światła, które świeci tak samo jasno we wszystkich kierunkach) ze strumieniem promieniowania (23.47, 21.31, 20.79) reprezentowany jako trójka RGB. Natężenie promieniowania tego źródła światła jest równe jego promieniowaniu we wszystkich kierunkach. Jednakże, gdy cieniujemy określony punkt $p$ na powierzchni, ze wszystkich możliwych kierunków światła na półkuli $\Omega$ tylko jeden przychodzący wektor kierunku $w_i$ bezpośrednio pochodzi z punktu źródła światła. Ponieważ mamy tylko jedno źródło światła w naszej scenie, zakładając, że znajduje się w jednym miejscu w przestrzeni, wszystkie inne możliwe kierunki światła mają zerową jasność obserwowaną na powierzchni punktu $p$:
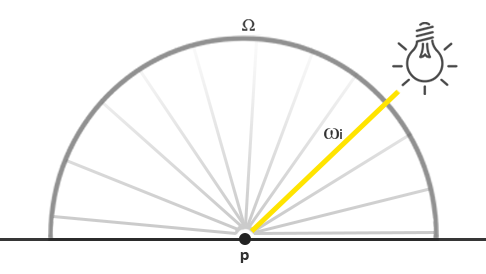
Jeśli na początku założymy, że tłumienie światła (przyciemnianie światła na odległość) nie ma wpływu na punktowe źródło światła, promieniowanie przychodzącego promienia światła jest takie samo niezależnie od tego, gdzie umieścimy światło (wyłączając skalowanie radiancji przez kąt padania $\cos\theta$). To dlatego, że światło punktowe ma taką samą intensywność promieniowania niezależnie od kąta, z którego patrzymy, efektywnie modelując jego natężenie promieniowania jako strumień promieniowania: wektor stały (23,47, 21,31, 20,79).
Radiancja również przyjmuje pozycję $p$ jako parametr, a ponieważ każde realistyczne punktowe źródło światła uwzględnia tłumienie (ang. attenuation), intensywność radiancji punktowego źródła światła jest skalowana za pomocą jakiejś odległości między punktem $p$ a źródłem światła. Następnie, w wyniku wyodrębnienia z pierwotnego równania radiancji, wynik jest skalowany przez iloczyn skalarny między wektorem normalnym powierzchni $n$ i kierunkiem światła $w_i$.
Mówiąc bardziej praktycznie: w przypadku bezpośredniego światła punktowego funkcja radiancji $L$ mierzy kolor światła, tłumionego wraz z odległością aż do $p$ i skalowaną przez $n \cdot w_i$, ale tylko dla pojedynczego promienia światła $w_i$, który trafia w $p$, który jest równy wektorowi kierunkowemu światła od $p$. To przekłada się na kod:
vec3 lightColor = vec3(23.47, 21.31, 20.79);
vec3 wi = normalize(lightPos - fragPos);
float cosTheta = max(dot(N, Wi), 0.0);
float attenuation = calculateAttenuation(fragPos, lightPos);
float radiance = lightColor * attenuation * cosTheta;
Poza inną terminologią, ten fragment kodu powinien być dla ciebie strasznie znajomy: tak właśnie robiliśmy (rozproszone/diffuse) oświetlenie do tej pory. Jeśli chodzi o oświetlenie bezpośrednie, luminancja jest obliczana podobnie do tego, jak obliczaliśmy oświetlenie, ponieważ tylko pojedynczy kierunek światła przyczynia się do radiancji powierzchni.
Zauważ, że to założenie jest prawdziwe, ponieważ światło punktowe jest nieskończenie małe i jest to tylko jeden punkt w przestrzeni. Gdybyśmy mieli modelować światło, które ma objętość, jego radiancja byłaby niezerowa w więcej niż jednym kierunku światła.
W przypadku innych rodzajów źródeł światła pochodzących z pojedynczego punktu, podobnie obliczamy radiancję. Na przykład, kierunkowe źródło światła ma stałą $w_i$ bez żadnego współczynnika tłumienia, a reflektor nie miałby stałej intensywności radiancji, ale byłby skalowany przez wektor kierunku reflektora.
Powoduje to również powrót do całki $\int$ po półkuli $\Omega$. Jak wiemy, pojedyncze pozycje wszystkich źródeł światła, które mają wpływ, podczas cieniowania pojedynczego punktu powierzchni, nie są wymagane, aby rozwiązać całkę. Możemy bezpośrednio wziąć (znaną) liczbę źródeł światła i obliczyć całkowite natężenie promieniowania, biorąc pod uwagę, że każde źródło światła ma tylko jeden kierunek światła, który wpływa na radiancję powierzchni. To sprawia, że PBR na bezpośrednich źródłach światła jest stosunkowo prosty, ponieważ musimy tylko iterować po źródłach światła, które mają w tym swój udział. Kiedy później uwzględnimy oświetlenie środowiskowe w tutorialach IBL, musimy wziąć pod uwagę całkę, ponieważ światło może pochodzić z dowolnego kierunku.
Model powierzchniowy PBR
Zacznijmy od napisania Fragment Shadera, który zaimplementuje wcześniej opisane modele PBR. Najpierw musimy zdefiniować odpowiednie dane wejściowe PBR wymagane do cieniowania powierzchni:
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;
uniform vec3 camPos;
uniform vec3 albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;
Przyjmujemy standardowe dane wejściowe obliczone z ogólnego Vertex Shadera i zestawu stałych właściwości materiału na powierzchni obiektu.
Następnie na początku Fragment Shadera wykonujemy zwykłe obliczenia wymagane dla dowolnego algorytmu oświetlenia:
void main()
{
vec3 N = normalize(Normal);
vec3 V = normalize(camPos - WorldPos);
[...]
}
Bezpośrednie oświetlenie
W przykładzie demonstracyjnym tego tutoriala mamy w sumie 4-punktowe światła, które bezpośrednio reprezentują natężenie oświetlenia sceny. Aby spełnić równanie odbicia, iterujemy po każdym źródle światła, obliczamy jego indywidualną radiancję i sumujemy jego udział, który zostaje przeskalowany przez BRDF i kąt padania światła. Możemy myśleć o pętli jako o rozwiązaniu całki $\int$ po $\Omega$ dla bezpośrednich źródeł światła. Najpierw obliczamy odpowiednie zmienne dla każdego światła:
vec3 Lo = vec3(0.0);
for(int i = 0; i < 4; ++i)
{
vec3 L = normalize(lightPositions[i] - WorldPos);
vec3 H = normalize(V + L);
float distance = length(lightPositions[i] - WorldPos);
float attenuation = 1.0 / (distance * distance);
vec3 radiance = lightColors[i] * attenuation;
[...]
Podczas obliczania oświetlenia w przestrzeni liniowej (będziemy poprawiać wartości gamma na końcu shadera) tłumimy źródła światła bardziej fizycznie poprawnie poprzez
Choć fizycznie poprawne, nadal możesz chcieć użyć wartości stałej, liniowej i kwadratowej równania tłumienia, które (choć nie jest poprawne fizycznie) może zaoferować ci znacznie większą kontrolę nad spadkiem energii światła.
Następnie, dla każdego światła, chcemy obliczyć pełny termin specular/lustrzany BRDF Cook-Torrance:
\[\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}\]Pierwszą rzeczą, którą chcemy zrobić, to obliczyć proporcję między odbiciem lustrzanym i rozproszonym, lub ile powierzchnia odbija światła w porównaniu z tym, jak bardzo załamuje światło. Wiemy z poprzedniego tutoriala, że równanie Fresnela obliczane jest tak:
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}
Przybliżenie Fresnela-Schlicka oczekuje parametru F0, który jest znany jako odbicie powierzchniowe przy zerowym kącie padania lub ile powierzchnia odbija światła, patrząc bezpośrednio na powierzchnię. F0 różni się w zależności od materiału i jest zabarwiony na metalach, tak jak to widać w dużych bazach materiałowych. W metalicznym potoku pracy PBR zakładamy, że większość powierzchni dielektrycznych wygląda wizualnie poprawnie ze stałą F0 równą 0.04, podczas gdy my określamy F0 dla powierzchni metalicznych, jak wtedy podawaliśmy przez wartość albedo. Przekłada się to na kod w następujący sposób:
vec3 F0 = vec3(0.04);
F0 = mix(F0, albedo, metallic);
vec3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);
Jak widać, dla powierzchni niemetalicznych F0 wynosi zawsze 0.04, podczas gdy my zmieniamy F0 na podstawie metaliczności powierzchni poprzez liniową interpolację między oryginalną wartością F0 i wartość albedo z uwzględnieniem właściwości metallic.
Biorąc pod uwagę $F$, pozostałe warunki do obliczenia to funkcja rozkładu normalnych $D$ i funkcja geometrii $G$.
W bezpośrednim Fragment Shaderze PBR ich odpowiednikami są:
float DistributionGGX(vec3 N, vec3 H, float roughness)
{
float a = roughness*roughness;
float a2 = a*a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH*NdotH;
float num = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return num / denom;
}
float GeometrySchlickGGX(float NdotV, float roughness)
{
float r = (roughness + 1.0);
float k = (r*r) / 8.0;
float num = NdotV;
float denom = NdotV * (1.0 - k) + k;
return num / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx2 = GeometrySchlickGGX(NdotV, roughness);
float ggx1 = GeometrySchlickGGX(NdotL, roughness);
return ggx1 * ggx2;
}
Należy zauważyć, że w przeciwieństwie do poprzedniego tutoriala, przekazujemy parametr chropowatości bezpośrednio do tych funkcji; w ten sposób możemy wprowadzić specyficzne dla danego terminu modyfikacje pierwotnej wartości szorstkości. Na podstawie obserwacji dokonanych przez firmę Disney i przyjętych przez Epic Games oświetlenie wydaje się bardziej poprawne zarówno pod względem geometrii, jak i rozkładu normalnych.
Po zdefiniowaniu obu funkcji obliczanie NDF i G-term w pętli odbicia jest proste:
float NDF = DistributionGGX(N, H, roughness);
float G = GeometrySmith(N, V, L, roughness);
Daje nam to wystarczająco dużo, aby obliczyć Cook-Torrance BRDF:
vec3 numerator = NDF * G * F;
float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0);
vec3 specular = numerator / max(denominator, 0.001);
Zwróć uwagę, że ograniczamy mianownik do 0.001, aby zapobiec dzieleniu przez zero w przypadku, gdy iloczyn skalarny zwróci wartość 0.0.
Teraz możemy w końcu obliczyć udział każdego światła w równaniu odbicia. Ponieważ wartość Fresnela odpowiada bezpośrednio $k_S$, możemy użyć $F$ do oznaczenia kontrybucji światła, które dociera do powierzchni. Z $k_S$ możemy następnie bezpośrednio obliczyć współczynnik załamania $k_D$:
vec3 kS = F;
vec3 kD = vec3(1.0) - kS;
kD *= 1.0 - metallic;
Jako, że kS reprezentuje energię światła, która zostaje odbita, pozostały stosunek energii światła jest światłem, które ulega załamaniu, które przechowujemy jako kD. Ponadto, ponieważ powierzchnie metalowe nie załamują światła, a zatem nie mają odbić rozproszonych, wymuszamy tę właściwość przez zerowanie kD, jeśli powierzchnia jest metaliczna. Daje nam to ostateczne dane potrzebne do obliczenia wyjściowej wartości współczynnika odbicia dla każdego światła:
const float PI = 3.14159265359;
float NdotL = max(dot(N, L), 0.0);
Lo += (kD * albedo / PI + specular) * radiance * NdotL;
}
Otrzymana wartość Lo, czyli wychodząca radiancja, jest faktycznie wynikiem całkowania równania odbicia $\int$ po $\Omega$. Tak naprawdę nie musimy próbować rozwiązywać całki dla wszystkich możliwych kierunków światła, ponieważ dokładnie znamy 4 kierunki światła, które mogą wpłynąć na fragment. Z tego powodu możemy bezpośrednio iterować po tych przychodzące kierunkach światła, określonych np. za pomocą liczby świateł na scenie.
Pozostało tylko dodać (improwizowane) pojęcie ambientu do wyniku oświetlenia bezpośredniego Lo i mamy finalny kolor oświetlonego fragmentu:
vec3 ambient = vec3(0.03) * albedo * ao;
vec3 color = ambient + Lo;
Renderowanie liniowe i HDR
Do tej pory założyliśmy, że wszystkie nasze obliczenia są w liniowej przestrzeni barw i musimy to uwzględnić poprzez korekcję gamma na końcu shadera. Obliczanie oświetlenia w przestrzeni liniowej jest niezwykle ważne, ponieważ PBR wymaga, aby wszystkie dane wejściowe były liniowe, nieuwzględnienie tego spowoduje nieprawidłowe oświetlenie. Dodatkowo, chcemy, aby parametry wejściowe światła były zbliżone do ich fizycznych odpowiedników, tak aby ich radiancja lub wartości kolorów mogły się znacznie różnić w szerokim spektrum wartości. W rezultacie Lo może szybko osiągać duże wartości, a następnie zostaje obcięte do wartości między 0.0 a 1.0 z powodu domyślnego wyjścia LDR (Low Dynamic Range). Naprawimy to, przyjmując wartość Lo, a ton lub ekspozycję prawidłowo odwzorowujemy w HDR (High Dynamic Range) na LDR przed korektą gamma:
color = color / (color + vec3(1.0));
color = pow(color, vec3(1.0/2.2));
W tym miejscu mapujemy kolor HDR za pomocą operatora Reinharda, zachowując HDR możliwie silnie zmieniającego się natężenia promieniowania, po którym poprawiamy gammę koloru. Nie mamy oddzielnego bufora ramki ani etapu post-processingu, więc możemy bezpośrednio zastosować zarówno krok tone mappingu, jak i krok korekcji gamma bezpośrednio na końcu Fragment Shadera.

Uwzględnienie zarówno liniowej przestrzeni barw, jak i HDR jest niezwykle ważne w procesie PBR. Bez nich nie można poprawnie uchwycić szczegółów o różnym natężeniu światła, a obliczenia są niepoprawne, a zatem nieprzyjemne wizualnie.
Pełny kod shadera oświetlenia PBR
Pozostaje nam tylko przekazać końcowy kolor HDR do Fragment Shadera. Dla kompletności pełna funkcja
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;
// parametry materiałowe
uniform vec3 albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;
// światła
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];
uniform vec3 camPos;
const float PI = 3.14159265359;
float DistributionGGX(vec3 N, vec3 H, float roughness);
float GeometrySchlickGGX(float NdotV, float roughness);
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness);
void main()
{
vec3 N = normalize(Normal);
vec3 V = normalize(camPos - WorldPos);
vec3 F0 = vec3(0.04);
F0 = mix(F0, albedo, metallic);
// równanie odbicia
vec3 Lo = vec3(0.0);
for(int i = 0; i < 4; ++i)
{
// obliczy radiancję per-światło
vec3 L = normalize(lightPositions[i] - WorldPos);
vec3 H = normalize(V + L);
float distance = length(lightPositions[i] - WorldPos);
float attenuation = 1.0 / (distance * distance);
vec3 radiance = lightColors[i] * attenuation;
// cook-torrance brdf
float NDF = DistributionGGX(N, H, roughness);
float G = GeometrySmith(N, V, L, roughness);
vec3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);
vec3 kS = F;
vec3 kD = vec3(1.0) - kS;
kD *= 1.0 - metallic;
vec3 numerator = NDF * G * F;
float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0);
vec3 specular = numerator / max(denominator, 0.001);
// dodaj do wynikowej radiancji Lo
float NdotL = max(dot(N, L), 0.0);
Lo += (kD * albedo / PI + specular) * radiance * NdotL;
}
vec3 ambient = vec3(0.03) * albedo * ao;
vec3 color = ambient + Lo;
color = color / (color + vec3(1.0));
color = pow(color, vec3(1.0/2.2));
FragColor = vec4(color, 1.0);
}
Mam nadzieję, że dzięki teorii z poprzedniego samouczka i znajomości równania odbicia ten shader nie powinien już być tak zniechęcający. Jeśli weźmiemy ten shader, 4-punktowe światła i całkiem sporo sfer, w których odpowiednio zmieniamy ich wartości metaliczne i chropowatości odpowiednio na pionowej i poziomej osi, otrzymamy coś takiego:

Od dołu do góry wartość metaliczna mieści się w zakresie od 0.0 do 1.0, a chropowatość wzrasta od lewej do prawej od 0.0 do 1.0. Widać, że zmieniając tylko te dwa proste do zrozumienia parametry, możemy już wyświetlić szeroką gamę różnych materiałów.
Możesz znaleźć pełny kod źródłowy demo tutaj.
Teksturowane PBR
Rozszerzając system tak, by akceptował jego parametry powierzchniowe jako tekstury zamiast wartości uniform dają nam kontrolę na poziomie fragmentów nad właściwościami materiału powierzchni:
[...]
uniform sampler2D albedoMap;
uniform sampler2D normalMap;
uniform sampler2D metallicMap;
uniform sampler2D roughnessMap;
uniform sampler2D aoMap;
void main()
{
vec3 albedo = pow(texture(albedoMap, TexCoords).rgb, 2.2);
vec3 normal = getNormalFromNormalMap();
float metallic = texture(metallicMap, TexCoords).r;
float roughness = texture(roughnessMap, TexCoords).r;
float ao = texture(aoMap, TexCoords).r;
[...]
}
Zauważ, że tekstury albedo, które pochodzą od artystów są generalnie tworzone w przestrzeni sRGB, dlatego najpierw przekształcamy je w przestrzeń liniową przed użyciem albedo w naszych obliczeniach oświetlenia. W oparciu o system, którego artyści używają do generowania map okluzji otoczenia, możesz również przekonwertować te z sRGB do przestrzeni liniowej. Mapy metaliczne i chropowatości są prawie zawsze tworzone w przestrzeni liniowej.
Zastąpienie właściwości materiałowych poprzedniego zestawu sfer za pomocą tekstur, pokazuje już znaczną poprawę wizualną w stosunku do poprzednich algorytmów oświetleniowych, z których korzystaliśmy:

Możesz znaleźć pełny kod źródłowy oteksturowanej wersji demonstracyjnej tutaj oraz zestaw tekstur, którego użyłem tutaj (z białą mapą AO). Należy pamiętać, że powierzchnie metalowe wydają się zbyt ciemne w warunkach bezpośredniego oświetlenia, ponieważ nie mają odbicia rozproszonego. Wyglądają bardziej poprawnie, gdy uwzględnimy lustrzane światło otoczenia, na czym skupimy się w następnych tutorialach.
Chociaż nie jest to tak imponujące wizualnie, jak niektóre z dem PBR, które możesz znaleźć w Internecie, zważywszy, że nie mamy jeszcze oświetlenia opartego na obrazie (IBL) zaimplementowanego w naszym systemie, to wciąż jest on rendererem opartym na fizyce, a nawet bez IBL zobaczysz, że twoje oświetlenie wygląda o wiele bardziej realistycznie.