This is the Polish translation of PBR/IBL/Diffuse-irradiance article of learnopengl.com tutorial series.
IBL lub
Ponieważ algorytmy oświetlenia opartego na obrazie wychwytują oświetlenie niektórych (globalnych) środowisk, jego wejście jest uważane za bardziej precyzyjną formę oświetlenia otoczenia, nawet z grubsza przybliżoną orientację globalnego oświetlenia. To sprawia, że IBL jest interesujący dla PBR, ponieważ obiekty wyglądają znacznie lepiej, gdy uwzględnimy oświetlenie otoczenia.
Aby rozpocząć wprowadzanie IBL do naszego systemu PBR, ponownie przyjrzyjmy się równaniu odbicia:
\[L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]Jak opisano wcześniej, naszym głównym celem jest rozwiązanie całki dla wszystkich kierunków światła $w_i$ na półkuli $\Omega$. Rozwiązanie całki w poprzednim tutorialu było łatwe, ponieważ znaliśmy wcześniej dokładnie kilka kierunków światła $w_i$. Tym razem jednak każdy kierunek światła $w_i$ pochodzący z otaczającego środowiska może potencjalnie mieć nieco radiancji, co sprawia, że rozwiązanie problemu nie jest takie proste. Daje nam to dwa główne wymagania dotyczące rozwiązania całki:
- Potrzebujemy jakiegoś sposobu na pobranie radiancji sceny z dowolnego wektora kierunku $w_i$.
- Rozwiązanie całki musi być szybkie i realizowane w czasie rzeczywistym.
Pierwszy wymóg jest stosunkowo łatwy. Wspomnieliśmy już o tym, ale jednym ze sposobów reprezentacji oświetlenia otoczenia lub sceny jest forma (przetworzonej) mapa środowiska. Biorąc pod uwagę taką cubemapę, możemy zwizualizować każdy teksel mapy jako jedno źródło światła. Poprzez próbkowanie tej cubemapy z dowolnym wektorem kierunku $w_i$ otrzymujemy radiancję sceny z tego kierunku.
Otrzymanie radiancji sceny z dowolnego wektora kierunku $w_i$ jest wtedy tak proste, jak:
vec3 radiance = texture(_cubemapEnvironment, w_i).rgb;
Mimo to, rozwiązanie całki wymaga od nas spróbkowania mapy środowiska nie tylko z jednego kierunku, ale ze wszystkich możliwych kierunków $w_i$ na półkuli $\Omega$, co jest zbyt drogie dla każdego wywołania Fragment Shadera. Aby rozwiązać problem w bardziej skuteczny sposób, będziemy chcieli pre-processować lub
Przyjrzawszy się równaniu odbicia, stwierdzamy, że komponenty diffuse $k_d$ i specular $k_s$ BRDF są niezależne od siebie i możemy podzielić całkę na dwie części:
\[L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i + \int\limits_{\Omega} (k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]Dzieląc całkę na dwie części możemy indywidualnie skupić się zarówno na komponencie diffuse, jak i specular; główny temat tego samouczka dotyczy całki diffuse.
Przyjrzyjmy się bliżej całce diffuse, stwierdzając, że termin diffuse lamberta jest terminem stałym (kolor $c$, współczynnik załamania $k_d$ i $\pi$ są stałe względem całki) i nie zależy od żadnej ze zmiennych całkowych. Biorąc to pod uwagę, możemy przenieść stały termin na zewnątrz całki diffuse:
\[L_o(p,\omega_o) = k_d\frac{c}{\pi} \int\limits_{\Omega} L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]Daje nam to całkę, która zależy tylko od $w_i$ (zakładając, że $p$ znajduje się w centrum mapy środowiska). Dzięki tej wiedzy możemy obliczyć lub wstępnie obliczyć nową cubemapę, która przechowuje dla każdego kierunku próbkowania (lub tekselu) $w_o$ wynikiem całki diffuse przez
Konwolucja stosuje pewne obliczenia do każdego wpisu w zbiorze danych, biorąc pod uwagę wszystkie inne wpisy w zbiorze danych; zestaw danych będący radiancją sceny lub mapą otoczenia. W związku z tym dla każdego kierunku próbkowania w cubemapie uwzględniamy wszystkie inne kierunki próbkowania na półkuli $\Omega$.
Aby wykonać splot na mapie środowiska, rozwiązujemy całkę dla każdego wyjściowego kierunku próbkowania $w_o$ poprzez dyskretne próbkowanie dużej liczby kierunków $w_i$ na półkuli $\Omega$ i uśrednianie ich radiancji. Półkula, na bazie której budujemy kierunki próbkowania $w_i$ jest zorientowana w stronę wyjściowego kierunku próbkowania $w_o$, na którym wykonujemy splot.
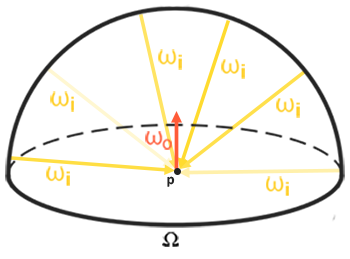
Ta wstępnie obliczona cubemapa, która dla każdego kierunku próbkowania $w_o$ przechowuje wynik całkowy, może być uważana za wstępnie obliczoną sumę wszystkich pośrednich rozproszonych świateł sceny uderzającej w pewną powierzchnię ustawioną wzdłuż kierunku $w_o$. Taka mapa jest znana jako
Równanie radiancji zależy również od położenia $p$, które, jak zakładaliśmy, znajduje się w centrum mapy irradiancji. Oznacza to, że całe rozproszone światło pośrednie musi pochodzić z pojedynczej mapy środowiska, która może zakłócić iluzję rzeczywistości (szczególnie w pomieszczeniu). Silniki renderujące rozwiązują to poprzez umieszczanie
Poniżej znajduje się przykład mapy środowiskowej i wynikającej z niej mapy irradiancji (dzięki uprzejmości wave engine), uśredniającej radiancję sceny dla każdego kierunku $w_o$.

Przechowując wynik splotu w każdym tekselu cubemapy (w kierunku $w_o$), mapa irradiancji wyświetla coś jak uśredniony kolor lub oświetlenie mapy otoczenia. Próbkowanie w dowolnym kierunku z tej mapy otoczenia da nam irradiancję sceny z tego konkretnego kierunku.
PBR i HDR
Krótko omówiliśmy to w samouczku oświetlenie PBR: uwzględnienie HDR dla oświetlenia Twojej sceny w potoku PBR jest niezwykle ważne. Ponieważ PBR opiera większość danych wejściowych na rzeczywistych właściwościach fizycznych i pomiarach, ma sens dopasowanie wejściowych danych światła do ich fizycznych odpowiedników. Bez względu na to, czy sami wybieramy wartość strumienia promieniowania każdego światła, czy używamy jego bezpośredniego odpowiednika fizycznego, różnica pomiędzy zwykłą żarówką a słońcem jest znacząca. Bez pracy w HDR nie można poprawnie określić intensywności każdego światła z osobna.
Zatem PBR i HDR idą w parze, ale jak to wszystko ma związek z oświetleniem opartym na obrazie? Widzieliśmy w poprzednim tutorialu, że stosunkowo łatwo jest uzyskać PBR działający w HDR. Jednakże, patrząc na oświetlenie oparte na obrazie, opieramy średnią intensywność światła otoczenia na wartościach kolorów mapy środowiska. Potrzebujemy w jakiś sposób, aby zapisać wartości oświetlenia HDR w mapie środowiska.
Mapy środowiskowe, których używaliśmy do tej pory dla cubemap (używane jako skyboxy) mają wartości LDR. Bezpośrednio użyliśmy ich wartości kolorów z poszczególnych obrazów ścianek, w zakresie od 0.0 do 1.0, i przetwarzaliśmy je w niezmienionej postaci. Chociaż może to działać dobrze, to przy przyjmowaniu ich jako fizycznych parametrów wejściowych nie będzie to dawać dobrych rezultatów.
Format plików HDR radiancji
Format pliku radiancji (z rozszerzeniem .hdr) przechowuje pełną mapę środowiska z wszystkimi 6 ściankami jako danymi zmiennoprzecinkowymi, pozwalając każdemu określić wartości kolorów poza zakresem 0.0 do 1.0, aby nadać światłom poprawne natężenie kolorów. Format pliku wykorzystuje również sprytny trik do przechowywania każdej wartości zmiennoprzecinkowej nie jako 32-bitową wartość na kanał, ale 8 bitów na kanał przy użyciu kanału alfa jako wykładnika (to przynosi utratę precyzji). Działa to całkiem dobrze, ale wymaga, aby program parsujący ponownie przekonwertował każdy kolor na ich odpowiednik zmiennoprzecinkowy.
Istnieje wiele map środowiska HDR radiancji, dostępnych za darmo ze źródeł takich jak archiwum sIBL, z którego można zobaczyć przykład poniżej:

Może to nie być dokładnie to, czego się spodziewałeś, ponieważ obraz wydaje się zniekształcony i nie pokazuje żadnej z 6 pojedynczych ścianek cubemapy, które widzieliśmy wcześniej. Ta mapa środowiskowa jest projekcją ze sfery na płaszczyznę, dzięki czemu możemy łatwiej zapisać środowisko w jednym obrazie zwanym
HDR i stb_image.h
Ładowanie obrazów HDR bezpośrednio wymaga pewnej wiedzy na temat format pliku, co nie jest zbyt trudne, ale uciążliwe. Na szczęście dla nas, popularna biblioteka stb_image.h obsługuje ładowanie obrazów HDR bezpośrednio jako tablicę wartości zmiennoprzecinkowych, która doskonale pasuje do naszych potrzeb. Z dodanym do projektu stb_image ładowanie obrazu HDR jest teraz proste:
#include "stb_image.h"
[...]
stbi_set_flip_vertically_on_load(true);
int width, height, nrComponents;
float *data = stbi_loadf("newport_loft.hdr", &width, &height, &nrComponents, 0);
unsigned int hdrTexture;
if (data)
{
glGenTextures(1, &hdrTexture);
glBindTexture(GL_TEXTURE_2D, hdrTexture);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, width, height, 0, GL_RGB, GL_FLOAT, data);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
stbi_image_free(data);
}
else
{
std::cout << "Failed to load HDR image." << std::endl;
}
stb_image.h automatycznie mapuje wartości HDR do listy wartości zmiennoprzecinkowych: domyślnie 32 bity na kanał i 3 kanały na kolor. Jest to wszystko, czego potrzebujemy, aby zapisać mapę środowiska w kształcie prostokąta HDR w teksturę zmiennoprzecinkową 2D.
Od Equirectangular do Cubemapy
Możliwe jest bezpośrednie wykorzystanie mapy equirectangular do próbkowania mapy środowiska, ale operacje te mogą być stosunkowo kosztowne, w takim przypadku bezpośrednie próbkowanie z cubemapy jest bardziej wydajne. W związku z tym, w tym samouczku najpierw przekształcimy obraz equirectangular w cubemapę w celu dalszego przetwarzania. Zwróć uwagę, że w tym procesie pokazujemy również, jak próbkować mapę equirectangular tak, jakby była mapą środowiska 3D, w którym to przypadku możesz wybrać dowolny sposób.
Aby przekonwertować obraz equirectangular na cubemapę, musimy wyrenderować sześcian (jednostkowy) i rzutować mapę equirectangular na wszystkie powierzchnie sześcianu od wewnątrz i wykonać 6 zdjęć każdej ściance sześcianu. Vertex Shader tej kostki po prostu renderuje kostkę taką jaka jest i przekazuje jej lokalne pozycje do Fragment Shadera jako wektora próbkowania 3D:
#version 330 core
layout (location = 0) in vec3 aPos;
out vec3 localPos;
uniform mat4 projection;
uniform mat4 view;
void main()
{
localPos = aPos;
gl_Position = projection * view * vec4(localPos, 1.0);
}
W przypadku Fragment Shadera kolorujemy każdą część sześcianu, tak jakbyśmy starannie nakleili mapę equirectangular na każdej ściance sześcianu. Aby to osiągnąć, bierzemy przykładowy kierunek próbkowania fragmentu, interpolowany z położenia lokalnego sześcianu, a następnie używamy wektora kierunku i pewnej magii trygonometrii do spróbkowania mapy equirectangular, tak jakby była cubemapą. Bezpośrednio zapisujemy wynik na fragmencie sześcianu:
#version 330 core
out vec4 FragColor;
in vec3 localPos;
uniform sampler2D equirectangularMap;
const vec2 invAtan = vec2(0.1591, 0.3183);
vec2 SampleSphericalMap(vec3 v)
{
vec2 uv = vec2(atan(v.z, v.x), asin(v.y));
uv *= invAtan;
uv += 0.5;
return uv;
}
void main()
{
vec2 uv = SampleSphericalMap(normalize(localPos)); // upewnij się, że normalizujesz localPos
vec3 color = texture(equirectangularMap, uv).rgb;
FragColor = vec4(color, 1.0);
}
Jeśli wyrenderujesz sześcian na środku sceny, biorąc pod uwagę mapę equirectangular HDR, otrzymasz coś, co wygląda tak:

To pokazuje, że zmapowaliśmy obraz equirectangular na kształt sześcienny, ale nie pomaga nam on jeszcze w przekształceniu źródłowego obrazu HDR w teksturę cubemapy. Aby to osiągnąć, musimy wyrenderować tę samą kostkę 6 razy, patrząc na każdą pojedynczą ściankę sześcianu podczas rejestrowania efektu wizualnego za pomocą obiektu framebuffer:
unsigned int captureFBO, captureRBO;
glGenFramebuffers(1, &captureFBO);
glGenRenderbuffers(1, &captureRBO);
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, captureRBO);
Oczywiście, następnie generujemy również odpowiednią cubemapę, wstępnie alokującą pamięć dla każdej z jej 6 ścianek:
unsigned int envCubemap;
glGenTextures(1, &envCubemap);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
for (unsigned int i = 0; i < 6; ++i)
{
// note that we store each face with 16 bit floating point values
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F,
512, 512, 0, GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
Pozostało tylko przekonwertować teksturę equirectangular 2D na ścianki cubemapy.
Nie będę omawiać szczegółów, ponieważ szczegóły kodu zostały omówione wcześniej w tutorialach Framebuffer i Cienie Świateł Punktowych, ale sprowadza się to wszystko do ustawienia 6 różnych macierzy widoku dla każdej ścianki sześcianu, biorąc pod uwagę macierz projekcji o FoV 90 stopni, aby uchwycić całą ściankę i renderujemy sześcian 6 razy przechowując wyniki w zmiennoprzecinkowym framebufferze:
glm::mat4 captureProjection = glm::perspective(glm::radians(90.0f), 1.0f, 0.1f, 10.0f);
glm::mat4 captureViews[] =
{
glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 1.0f, 0.0f, 0.0f), glm::vec3(0.0f, -1.0f, 0.0f)),
glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(-1.0f, 0.0f, 0.0f), glm::vec3(0.0f, -1.0f, 0.0f)),
glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, 1.0f, 0.0f), glm::vec3(0.0f, 0.0f, 1.0f)),
glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, -1.0f, 0.0f), glm::vec3(0.0f, 0.0f, -1.0f)),
glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, 0.0f, 1.0f), glm::vec3(0.0f, -1.0f, 0.0f)),
glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, 0.0f, -1.0f), glm::vec3(0.0f, -1.0f, 0.0f))
};
// przekonwertuj mapę środowiskową equirectangular HDR na odpowiednik cubemapy
equirectangularToCubemapShader.use();
equirectangularToCubemapShader.setInt("equirectangularMap", 0);
equirectangularToCubemapShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, hdrTexture);
glViewport(0, 0, 512, 512); // nie zapomnij skonfigurować viewportu do wymiarów ścianki cubemapy.
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
for (unsigned int i = 0; i < 6; ++i)
{
equirectangularToCubemapShader.setMat4("view", captureViews[i]);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,
GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, envCubemap, 0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
renderCube(); // renderuje kostkę 1x1
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);
Bierzemy załącznik koloru bufora ramki i zmieniamy jej docelowy teksturę dla każdej powierzchni cubemapy, bezpośrednio renderując scenę do jednej ze ścianek cubemapy. Po zakończeniu tej procedury (co musimy zrobić tylko raz), mapa cubemap envCubemap powinna być zmodyfikowaną wersją naszego oryginalnego obrazu HDR.
Przetestujmy tę cubemapę, pisząc bardzo prosty Fragment Shader skyboxa, aby wyświetlić mapę wokół nas:
#version 330 core
layout (location = 0) in vec3 aPos;
uniform mat4 projection;
uniform mat4 view;
out vec3 localPos;
void main()
{
localPos = aPos;
mat4 rotView = mat4(mat3(view)); // remove translation from the view matrix
vec4 clipPos = projection * rotView * vec4(localPos, 1.0);
gl_Position = clipPos.xyww;
}
Zwróć uwagę na sztuczkę z xyww, która zapewnia, że wartość głębi wyrenderowanych fragmentów kostki zawsze będzie miała wartości 1.0, co jest maksymalną wartością głębi opisaną w tutorialu Cubemap. Zauważ, że musimy zmienić funkcję porównania głębokości na GL_LEQUAL:
glDepthFunc(GL_LEQUAL);
Następnie Fragment Shader bezpośrednio pobiera mapę środowiska, używając położenia lokalnego fragmentu kostki:
#version 330 core
out vec4 FragColor;
in vec3 localPos;
uniform samplerCube environmentMap;
void main()
{
vec3 envColor = texture(environmentMap, localPos).rgb;
envColor = envColor / (envColor + vec3(1.0));
envColor = pow(envColor, vec3(1.0/2.2));
FragColor = vec4(envColor, 1.0);
}
Próbkujemy mapę środowiska za pomocą interpolowanych pozycji wierzchołków sześcianu, które bezpośrednio odpowiadają wektorowi kierunku próbkowania. Widząc, że komponenty translacji kamery są ignorowane, renderowanie kostki za pomocą tego shadera powinno zapewnić, że mapa środowiska będzie nieruchomym tłem. Zwróć też uwagę, że kiedy bezpośrednio wysyłamy wartości HDR mapy środowiska do domyślnego bufora ramki LDR, chcemy odpowiednio odwzorować wartości kolorów. Co więcej, prawie wszystkie mapy HDR są domyślnie w liniowej przestrzeni kolorów, więc przed zapisaniem do domyślnego bufora ramki musimy zastosować korekcję gamma.
Teraz renderowanie mapy środowiska powinno wyglądać mniej więcej tak:

Cóż… jest tego trochę do konfiguracji, ale udało nam się odczytać mapę środowiska HDR, przekonwertować ją z jej mapowania equirectangular do cubemapy i przekształcić ją w skybox. Ponadto ustawiliśmy mały system do renderowania wszystkich 6 ścianek cubemapy, którego będziemy potrzebować, gdy ponownie będziemy chcieli wykonać
Konwolucja cubemapy
Zgodnie z opisem z początku samouczka, naszym głównym celem jest rozwiązanie całki dla wszystkich pośredniego oświetlenia diffuse, biorąc pod uwagę natężenie oświetlenia sceny w postaci mapy środowiska. Wiemy, że możemy uzyskać radiancję sceny $L(p, w_i)$ w określonym kierunku poprzez próbkowanie mapy środowiska HDR w kierunku $w_i$. Aby rozwiązać całkę, musimy pobrać radiancję sceny ze wszystkich możliwych kierunków w obrębie półkuli $\Omega$ dla każdego fragmentu.
Jest to jednak niemożliwe do obliczenia, by spróbkować oświetlenia otoczenia z każdego możliwego kierunku w $\Omega$, liczba możliwych kierunków jest teoretycznie nieskończona. Możemy jednak przybliżyć liczbę kierunków, biorąc skończoną liczbę kierunków lub próbek, rozmieszczonych równomiernie lub wylosowanych z półkuli, aby uzyskać dość dokładne przybliżenie irradiancji, rozwiązując całkę $\int$ dyskretnie.
Jednak wciąż jest to zbyt kosztowne, aby zrobić to dla każdego fragmentu w czasie rzeczywistym, ponieważ liczba próbek wciąż musi być znacznie duża, aby uzyskać przyzwoite wyniki, dlatego chcemy to wstępnie obliczyć. Ponieważ orientacja półkuli decyduje o tym, gdzie będziemy przechwytywać irradiancję, możemy wstępnie obliczyć irradiancję dla każdej możliwej orientacji półkuli zorientowanej wokół wszystkich wychodzących kierunków $w_o$:
\[L_o(p,\omega_o) = k_d\frac{c}{\pi} \int\limits_{\Omega} L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]Biorąc pod uwagę dowolny wektor kierunkowy $w_i$, możemy następnie pobrać wstępnie obliczoną mapę irradiancji w celu uzyskania całkowitej irradiancji diffuse z kierunku $w_i$. Aby określić ilość pośredniego światła rozproszonego (irradiantowego) na powierzchni fragmentu, pobieramy całkowitą irradiancje z półkuli zorientowanej wokół jej wektora normalnego powierzchni. Uzyskanie irradiancji sceny jest wtedy tak proste, jak:
vec3 irradiance = texture(irradianceMap, N);
Teraz, aby wygenerować mapę irradiancji, musimy wykonać splot na oświetleniu otoczenia jakby było one przekształcone w cubemapę. Biorąc pod uwagę, że dla każdego fragmentu półkula powierzchni jest zorientowana zgodnie z wektorem normalnym $N$, konwolucja cubemapy równa się obliczeniu całkowitej uśrednionej radiancji każdego kierunku $w_i$ w półkuli $\Omega$ zorientowanej wzdłuż $N$.
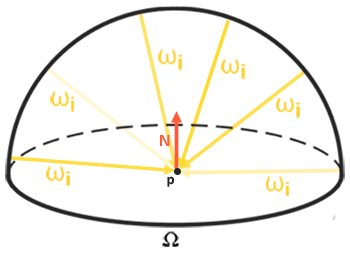
Na szczęście wszystkie kłopotliwe ustawienia w tym samouczku nie poszły na marne, ponieważ możemy teraz bezpośrednio wziąć przekształconą cubemapę, wykonać na niej splot w Fragment Shaderze i przechwycić jej wynik jako nową cubemapę, używając bufora ramki, który renderuje do wszystkich 6 ścianek. Jak już ustaliliśmy, aby konwertować mapę środowiska equirectangular na cubemapę, możemy podejść do problemu dokładnie tak samo, ale użyć innego Fragment Shadera:
#version 330 core
out vec4 FragColor;
in vec3 localPos;
uniform samplerCube environmentMap;
const float PI = 3.14159265359;
void main()
{
// kierunek próbki jest równy orientacji półkuli
vec3 normal = normalize(localPos);
vec3 irradiance = vec3(0.0);
[...] // kod splotu
FragColor = vec4(irradiance, 1.0);
}
Z environmentMap będącą cubemapą HDR konwertowaną z mapy środowiska equirectangular HDR.
Istnieje wiele sposobów konwolucji mapy środowiska, ale w tym samouczku wygenerujemy ustaloną liczbę wektorów próbkowania dla każdego teksela cubemapy wzdłuż półkuli $\Omega$ zorientowanej wokół kierunku próbkowania i uśrednimy wyniki. Ustalona ilość wektorów próbkowania będzie równomiernie rozłożona wewnątrz półkuli. Zauważ, że całka jest funkcją ciągłą i dyskretnie próbkując jej funkcję z ustaloną ilością wektorów próbkowania będzie jej przybliżeniem. Im więcej używanych wektorów próbkowania, tym lepiej przybliżamy całkę.
Całka $\int$ równania odbicia obraca się wokół kąta bryłowego $dw$, z którym trudno jest pracować. Zamiast całkowania za pomocą kąta bryłowego $dw$ całkujemy z odpowiednimi współrzędnymi sferycznymi $\theta$ i $\phi$.
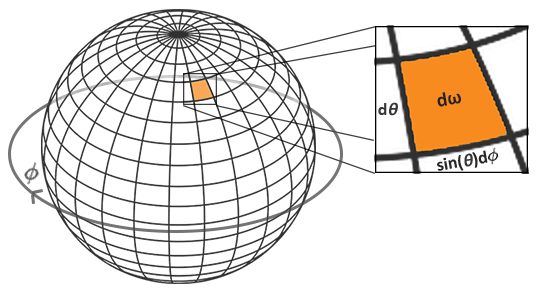
Używamy kąta polarnego azymutu $\phi$ do próbkowania wokół pierścienia półkuli między $0$ a $2 \pi$, i używamy kąta nachylenia zenitu $\theta$ od $0$ do $\frac{1}{2} \pi$ do próbkowania rosnących pierścieni półkuli. To da nam zaktualizowaną całkę odbicia:
\[L_o(p,\phi_o, \theta_o) = k_d\frac{c}{\pi} \int_{\phi = 0}^{2\pi} \int_{\theta = 0}^{\frac{1}{2}\pi} L_i(p,\phi_i, \theta_i) \cos(\theta) \sin(\theta) d\phi d\theta\]Rozwiązanie całki wymaga od nas pobrania określonej liczby dyskretnych próbek w obrębie półkuli $\Omega$ i uśrednienia ich wyników. Przekłada się to na następującą wersję dyskretną całki na podstawie sumy Riemanna, podając odpowiednio dyskretne próbki $n1$ i $n2$ dla każdej współrzędnej sferycznej:
\[L_o(p,\phi_o, \theta_o) = k_d\frac{c}{\pi} \frac{1}{n1 n2} \sum_{\phi = 0}^{n1} \sum_{\theta = 0}^{n2} L_i(p,\phi_i, \theta_i) \cos(\theta) \sin(\theta) d\phi d\theta\]Ponieważ dyskretnie próbkujemy obie wartości sferyczne, każda próbka będzie przybliżać lub uśredniać obszar na półkuli, jak pokazuje powyższy obraz. Zauważ, że (ze względu na ogólne właściwości kształtu sferycznego) dyskretny obszar próbki hemisfery staje się mniejszy, im wyższy jest kąt zenitu $\theta$, ponieważ obszary próbki zbiegają się w kierunku górnego środkowego wierzchołka. Aby zrekompensować mniejsze obszary, ważymy jego wkład, skalując obszar przez $\sin \theta$, wyjaśniając dodaną funkcję $\sin$.
Dyskretne próbkowanie półkuli z uwzględnieniem sferycznych współrzędnych całki dla każdego wywołania Fragment Shadera przekłada się na następujący kod:
vec3 irradiance = vec3(0.0);
vec3 up = vec3(0.0, 1.0, 0.0);
vec3 right = cross(up, normal);
up = cross(normal, right);
float sampleDelta = 0.025;
float nrSamples = 0.0;
for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
{
for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
{
// sferyczne wsp. do kartezjańskich (w przestrzeni stycznych - tangent space)
vec3 tangentSample = vec3(sin(theta) * cos(phi), sin(theta) * sin(phi), cos(theta));
// przestrzeń stycznych do przestrzeni świata
vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N;
irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta);
nrSamples++;
}
}
irradiance = PI * irradiance * (1.0 / float(nrSamples));
Określamy stałą wielkość delty sampleDelta, aby przejść po półkuli; zmniejszenie lub zwiększenie delty próbki zwiększy lub zmniejszy odpowiednio dokładność.
Z obu pętli bierzemy obie współrzędne sferyczne, aby przekształcić je w trójwymiarowy kartezjański wektor próbkowania, przekształcić próbkę z przestrzeni stycznych do przestrzeni świata i użyć tego wektora próbkowania do bezpośredniego pobrania próbki z mapy środowiska HDR. Każdy wynik próbkowania dodajemy do zmiennej irradiance, którą na koniec dzielimy przez całkowitą liczbę próbek, co daje nam średnią spróbkowaną irradiancję. Zwróć uwagę, że skalujemy próbkowaną wartość koloru przez cos(theta), ponieważ światło jest słabsze pod większymi kątami i przez sin(theta), aby uwzględnić mniejsze obszary próbek w wyższych obszarach półkuli.
Teraz pozostaje tylko ustawić kod renderujący OpenGL, abyśmy mogli wykonywać operację splotu na wcześniej przechwyconej envCubemap. Najpierw tworzymy cubemapę irradiancji (ponownie, musimy zrobić to tylko raz przed pętlą renderowania):
unsigned int irradianceMap;
glGenTextures(1, &irradianceMap);
glBindTexture(GL_TEXTURE_CUBE_MAP, irradianceMap);
for (unsigned int i = 0; i < 6; ++i)
{
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 32, 32, 0,
GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
Ponieważ mapa irradiancji uśrednia równomiernie całą otaczającą radiancję, nie ma wielu szczegółów o wysokiej częstotliwości, więc możemy przechowywać mapę w niskiej rozdzielczości (32x32) i pozwolić na jej liniowe filtrowanie. Następnie przeskalujemy bufor ramki do nowej rozdzielczości:
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 32, 32);
Za pomocą Fragment Shadera do obliczania splotu, konwolujemy mapę środowiska w podobny sposób, w jaki przechwyciliśmy mapę środowiska:
irradianceShader.use();
irradianceShader.setInt("environmentMap", 0);
irradianceShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glViewport(0, 0, 32, 32); // nie zapomnij skonfigurować veiwportu do wymiarów przechwytywania.
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
for (unsigned int i = 0; i < 6; ++i)
{
irradianceShader.setMat4("view", captureViews[i]);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,
GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, irradianceMap, 0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
renderCube();
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);
Teraz po tej funkcji powinniśmy mieć obliczoną mapę irradiancji, którą możemy bezpośrednio wykorzystać do oświetlenia rozproszonego opartego na obrazie. Aby sprawdzić, czy pomyślnie spletliśmy mapę środowiska, zamieńmy mapę środowiska na mapę irradiancji jako sampler skyboxa:

Jeśli wygląda na mocno zamazaną wersję mapy środowiska, udało ci się spleść mapę środowiska.
PBR i pośrednia irradiancja
Mapa irradiancji przedstawia rozproszoną część całki funkcji odbicia, zakumulowaną ze wszystkich otaczających świateł pośrednich. Widząc, że światło nie pochodzi z żadnych bezpośrednich źródeł światła, ale z otaczającego środowiska, traktujemy zarówno rozproszone, jak i lustrzane oświetlenie pośrednie jako oświetlenie otoczenia, zastępując wcześniej ustaloną stałą.
Najpierw należy dodać wstępnie obliczoną mapę irradiancji jako samplerCube:
uniform samplerCube irradianceMap;
Biorąc pod uwagę mapę irradiancji, która zawiera wszystkie pośrednie rozproszone światło sceny, odzyskanie irradiancji wpływającej na fragment jest tak proste, jak pojedyncze próbkowanie tekstury, biorąc pod uwagę wektor normalny powierzchni:
// vec3 ambient = vec3(0.03);
vec3 ambient = texture(irradianceMap, N).rgb;
Ponieważ oświetlenie pośrednie zawiera zarówno część rozproszoną, jak i lustrzaną, jak widzieliśmy w podzielonej wersji równania odbicia, musimy odpowiednio zważyć część rozproszoną. Podobnie do tego, co zrobiliśmy w poprzednim tutorialu, używamy równania Fresnela do określenia pośredniego współczynnika odbicia powierzchni, z którego uzyskujemy współczynnik załamania lub rozproszenia:
vec3 kS = fresnelSchlick(max(dot(N, V), 0.0), F0);
vec3 kD = 1.0 - kS;
vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse = irradiance * albedo;
vec3 ambient = (kD * diffuse) * ao;
Ponieważ światło otoczenia pochodzi ze wszystkich kierunków w obrębie półkuli zorientowanej wokół wektora normalnego N, nie ma jednego wektora połówkowego do określenia wartości Fresnela. Aby nadal symulować Fresnela, obliczamy Fresnela za pomocą kąta między wektorem normalnym a wektorem patrzenia. Jednak wcześniej użyliśmy wektora połówkowego mikrościanki, pod wpływem chropowatości powierzchni, jako parametru dla równania Fresnela. Ponieważ obecnie nie bierzemy pod uwagę żadnej szorstkości, współczynnik odbicia powierzchni zawsze będzie stosunkowo wysoki. Pośrednie światło ma takie same właściwości światło bezpośrednie, więc spodziewamy się, że szorstkie powierzchnie rzadziej odbijają światło na krawędziach powierzchni. Ponieważ nie uwzględniamy chropowatości powierzchni, pośrednia siła odbicia Fresnela wygląda blado na szorstkich powierzchniach niemetalowych (nieco przesadzone dla celów demonstracyjnych):

Możemy rozwiązać ten problem, wstrzykując pojęcie szorstkości do równania Fresnela-Schlicka jak opisał to Sébastien Lagarde:
vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness)
{
return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - cosTheta, 5.0);
}
Biorąc pod uwagę szorstkość powierzchni podczas obliczania Fresnela, kod oświetlenia otoczenia wygląda tak:
vec3 kS = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);
vec3 kD = 1.0 - kS;
vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse = irradiance * albedo;
vec3 ambient = (kD * diffuse) * ao;
Jak widać, rzeczywiste obliczenia oświetlenia oparte na obrazie są dość proste i wymagają tylko pojedynczego próbkowania tekstury; większość pracy polega na wstępnym obliczeniu lub splocie mapy środowiska na mapę irradiancji.
Jeśli weźmiemy pierwszą scenę z tutoriala oświetlenie PBR, gdzie każda kulka ma pionowo rosnącą metaliczność i poziomo rosnącą wartość chropowatości i dodamy rozproszone oświetlenie oparte na obrazie, to będzie to wyglądało mniej więcej tak:

Wciąż wygląda to trochę dziwnie, ponieważ bardziej metalowe kule wymagają jakiejś formy odbicia światła, aby zaczęły wyglądać jak metalowe powierzchnie (ponieważ metalowe powierzchnie nie odbijają rozproszonego światła), które w tej chwili (ledwo) dochodzi od punktowych źródeł światła. Niemniej jednak możesz już powiedzieć, że sfery pasują bardziej do otoczenia (szczególnie jeśli przełączasz się pomiędzy mapami środowiska), ponieważ powierzchnia reaguje odpowiednio na oświetlenie otoczenia.
Możesz znaleźć kompletny kod źródłowy omawianych tematów tutaj. W następnym samouczku dodamy pośrednią, lustrzaną część całki funkcji odbicia, gdzie zobaczymy prawdziwą moc PBR.
Więcej informacji
- Coding Labs: Physically based rendering: wprowadzenie do PBR oraz jak i dlaczego wygenerować mapę irradiancji.
- The Mathematics of Shading: krótkie wprowadzenie na temat kilku zagadnień opisywanych w tym kursie, a w szczególności na temat współrzędnych biegunowych i całek.