This is the Polish translation of PBR/IBL/Specular-IBL article of learnopengl.com tutorial series.
W poprzednim samouczku skonfigurowaliśmy PBR w połączeniu z oświetleniem opartym na obrazie poprzez wstępne obliczenie mapy irradiancji jako pośredniego oświetlenia rozproszonego. W tym samouczku skoncentrujemy się na części lustrzanej/specular równania odbicia:
\[L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]Zauważysz, że część lustrzana/specular Cook-Torrance’a (pomnożona przez $kS$) nie jest stałą w całce i jest zależna od kierunku światła, ale również od kierunku patrzenia. Próba rozwiązania całki dla wszystkich kierunków światła, w tym wszystkich możliwych kierunków patrzenia, jest przeciążeniem kombinatorycznym i jest to zbyt drogie do obliczenia w czasie rzeczywistym. Epic Games zaproponowało rozwiązanie, w którym udało im się pre-konwolować część lustrzaną w czasie rzeczywistym, biorąc pod uwagę kilka kompromisów, zwanych
Aproksymacja rozdzielonych sum dzieli część lustrzaną równania odbicia na dwie oddzielne części, które możemy konwolować pojedynczo, a następnie połączyć w shaderze PBR dla oświetlenia specular opartego na obrazie. Podobnie do tego, jak konwolowaliśmy mapę irradiancji, przybliżenie w postaci rozdzielonych sum wymaga mapy środowiska HDR jako wejścia do operatora splotu. Aby zrozumieć aproksymację rozdzielonych sum, ponownie przyjrzymy się równaniu odbicia, ale tym razem skupimy się tylko na części lustrzanej (wyodrębniliśmy część rozproszoną w poprzednim samouczku):
\[L_o(p,\omega_o) = \int\limits_{\Omega} (k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} L_i(p,\omega_i) n \cdot \omega_i d\omega_i = \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\]Z tych samych powodów (wydajnościowych), jak dla konwolucji irradiancji, nie możemy rozwiązać całki lustrzanej w czasie rzeczywistym i oczekiwać rozsądnej wydajności. Tak więc najlepiej byłoby wstępnie obliczyć tę całkę, by uzyskać coś w rodzaju mapy specular IBL i spróbkować tę mapę za pomocą wektora normalnego fragmentu. Jednak w tym przypadku robi się to nieco trudne. Udało nam się wstępnie obliczyć mapę irradiancji, jako że całka zależała tylko od $\omega_i$ i mogliśmy przenieść stałą albedo poza całkę. Tym razem całka zależy od czegoś więcej niż tylko $\omega_i$, jak wynika to z BRDF:
\[f_r(p, w_i, w_o) = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}\]Tym razem całka również zależy od $w_o$ i nie możemy tak naprawdę spróbkować wcześniej obliczonej cubemapy z dwoma wektorami kierunkowymi. Pozycja $p$ jest tutaj nieistotna, jak opisano to w poprzednim samouczku. Wstępne obliczenie tej całki dla każdej możliwej kombinacji $\omega_i$ i $\omega_o$ nie jest praktyczne w zastosowaniu dla aplikacji czasu rzeczywistego.
Przybliżenie rozdzielonych sum firmy Epic Games rozwiązuje ten problem, dzieląc wstępne obliczenia na dwie osobne części, które możemy później połączyć, aby otrzymać wynik, którego szukamy. Aproksymacja rozdzielonych sum dzieli całkę specular na dwie oddzielne całki:
\[L_o(p,\omega_o) = \int\limits_{\Omega} L_i(p,\omega_i) d\omega_i * \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i\]Pierwsza część (gdy jest spleciona) jest znana jako

Generujemy wektory próbkowania i ich siłę rozpraszania za pomocą funkcji rozkładu wektorów normalnych (NDF) funkcji BRDF Cook-Torrance’a, która przyjmuje jako dane wejściowe zarówno kierunek wektora normalnego, jak i kierunek patrzenia. Ponieważ nie znamy wcześniej kierunku patrzenia podczas splatania mapy środowiska, Epic Games dokonuje dalszego przybliżenia, zakładając, że kierunek patrzenia (a tym samym kierunek odbicia lustrzanego) jest zawsze równy wyjściowemu kierunkowi próbkowania $\omega_o$. Przekłada się to na następujący kod:
vec3 N = normalize(w_o);
vec3 R = N;
vec3 V = R;
W ten sposób konwolucja pre-filtrowania mapy środowiska nie musi być świadoma kierunku patrzenia. Oznacza to, że nie dostaniemy ładnych odbić lustrzanych podczas patrzenia pod kątem na odbicie lustrzane powierzchni, jak widać to na poniższym obrazku (dzięki uprzejmości artykułu Moving Frostbite to PBR); jest to jednak ogólnie uznane za przyzwoity kompromis:

Druga część równania jest równa części BRDF całki zwierciadlanej/specular. Jeśli udamy, że nadchodząca jasność jest całkowicie biała dla każdego kierunku (stąd $L (p, x) = 1.0$), możemy wstępnie obliczyć wartość BRDF z uwzględnieniem szorstkości wejściowej i kąta wejściowego między kierunkiem normalnej $n$ i kierunkiem światła $\omega_i$, lub $n \cdot \omega_i$. Epic Games przechowuje wstępnie obliczoną odpowiedź BRDF na każdą kombinację wektora normalnego i kierunku światła dla różnych wartości chropowatości w teksturach 2D (LUT) znanych jako mapa

Generujemy teksturę LUT, traktując współrzędną poziomą tekstury (w zakresie od 0.0 do 1.0) płaszczyzny jako wartość wejściową BRDF $n \cdot \omega_i$ i jej pionową współrzędną tekstury jako wartość chropowatości wejściowej. Dzięki tej mapie całkowania BRDF i pre-filtrowanej mapie środowiska możemy połączyć obie części, aby uzyskać wynik całki lustrzanej:
float lod = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
vec2 envBRDF = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y)
To powinno dać ci pewien przegląd tego, w jaki sposób aproksymacja dzielonych sum Epic Games z grubsza przybliża wynik części specular równania odbicia. Spróbujmy teraz sami zaimplementować te pre-konwolowane części.
Pre-filtrowanie mapy środowiska HDR
Pre-filtrowanie mapy środowiska jest dość podobne do tego, jak konwolowaliśmy mapę irradiancji. Różnica polega na tym, że obecnie obliczamy chropowatość i przechowujemy sekwencyjnie coraz bardziej ostrzejsze odbicia na kolejnych poziomach mipmap pre-filtrowanej mapy.
Najpierw musimy wygenerować nową cubemapę do przechowywania pre-filtrowanych danych mapy środowiska. Aby upewnić się, że przydzielamy wystarczającą ilość pamięci dla mipmap, wywołujemy funkcję
unsigned int prefilterMap;
glGenTextures(1, &prefilterMap);
glBindTexture(GL_TEXTURE_CUBE_MAP, prefilterMap);
for (unsigned int i = 0; i < 6; ++i)
{
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 128, 128, 0, GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glGenerateMipmap(GL_TEXTURE_CUBE_MAP);
Zauważ, że ponieważ planujemy próbkować mipmapy prefilterMap, musisz upewnić się, że jego filtr minifikacji/pomniejszania jest ustawiony na GL_LINEAR_MIPMAP_LINEAR, aby umożliwić filtrowanie trójliniowe. Przechowujemy wstępnie pre-filtrowane odbicia lustrzane każdej ścianki w rozdzielczości 128x128 jako rozdzielczość bazowej mipmapy. To może wystarczyć dla większości odbić, ale jeśli masz dużo gładkich materiałów (pomyśl o odbiciach samochodu), możesz zwiększyć rozdzielczość.
W poprzednim samouczku splataliśmy mapę środowiska, generując wektory próbkowania równomiernie rozłożone na półkuli $\Omega$ za pomocą współrzędnych sferycznych. Chociaż działa to dobrze dla irradiancji, dla odbić lustrzanych jest to mniej wydajne. Jeśli chodzi o odbicia lustrzane, w oparciu o chropowatość powierzchni, światło odbija się blisko lub w przybliżeniu wokół wektora odbicia $r$ względem wektora normalnego $n$, ale niemniej jednak (o ile powierzchnia nie jest ekstremalnie chropowata) wokół wektora odbicia:

Ogólny kształt możliwych wychodzących odbić światła jest znany jako
Jeśli chodzi o model mikropowierzchniowy, możemy sobie wyobrazić, że płat lustrzany jest orientacją odbicia wokół wektorów połówkowych dla pewnego kierunku światła. Ponieważ większość promieni światła trafia do płata lustrzanego odbijanego wokół wektorów połówkowych mikrościanek, to sensowne jest generowanie wektorów próbkowania w podobny sposób ze względu na to, że i tak większość z nich zostałaby zmarnowana. Ten proces jest znany jako
Całkowanie Monte Carlo i ważność próbkowania
Aby w pełni zrozumieć czym jest ważność próbkowania, najpierw zagłębimy się w konstrukcję matematyczną zwaną
Na przykład, powiedzmy, że chcesz policzyć średni wzrost wszystkich obywateli danego kraju. Aby uzyskać wynik, możesz zmierzyć każdego obywatela i uśrednić ich wzrost, który da dokładną odpowiedź, której szukasz. Ponieważ jednak większość krajów ma znaczną populację, nie jest to podejście realistyczne: wymagałoby to zbyt wiele wysiłku i czasu.
Innym podejściem jest wybór znacznie mniejszego całkowicie losowego (ang. unbiased) podzbioru tej populacji, zmierzenie ich wzrostu i uśrednienie wyników. Ta populacja może być tak mała, jak 100 osób. Chociaż nie jest to tak dokładne jak dokładna odpowiedź, otrzymasz odpowiedź, która jest relatywnie bliska prawdy. Jest to znane jako
Całkowanie Monte Carlo opiera się na prawie wielkich liczb i przyjmuje takie samo podejście do rozwiązywania całek. Zamiast rozwiązywania całki dla wszystkich możliwych (teoretycznie nieskończonych) wartości próbek $x$, po prostu wygeneruj $N$ losowo wybranych przykładowych wartości z całkowitej populacji i je uśrednij. Wraz ze wzrostem $N$ mamy gwarancję uzyskania wyniku bliższego dokładnej wartości całki:
\[O = \int\limits_{a}^{b} f(x) dx = \frac{1}{N} \sum_{i=0}^{N-1} \frac{f(x)}{pdf(x)}\]Aby rozwiązać całkę, pobieramy $N$ losowych próbek z populacji od $a$ do $b$, sumujemy je i dzielimy przez całkowitą liczbę próbek, aby je uśrednić. $Pdf$ oznacza
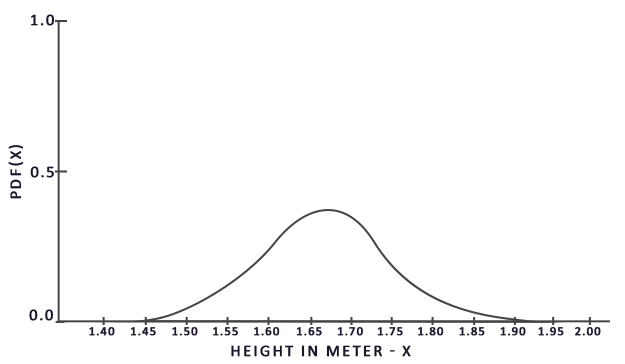
Z tego wykresu widać, że jeśli weźmiemy dowolną losową próbkę populacji, istnieje większa szansa na pobranie próbki osoby o wzroście 1.70, w porównaniu do niższego prawdopodobieństwa, że próbki osoby o wzroście 1.50.
Jeśli chodzi o całkowanie Monte Carlo, niektóre próbki mogą mieć większe prawdopodobieństwo wygenerowania niż inne. Dlatego dla każdego ogólnego oszacowania Monte Carlo dzielimy lub mnożymy próbkowaną wartość przez prawdopodobieństwo próbki zgodnie z pdf. Jak dotąd, w każdym z naszych przypadków oszacowania całki, wygenerowane przez nas próbki były generowane jednolicie, mając taką samą szansę na wygenerowanie. Nasze dotychczasowe szacunki były
Jednak niektóre estymatory Monte Carlo są
Całkowanie Monte Carlo jest dość powszechne w grafice komputerowej, ponieważ jest to dość intuicyjny sposób przybliżania całek ciągłych w dyskretny i wydajny sposób: weź dowolny obszar/objętość, aby pobierać próbki (jak półkula $\Omega$), wygeneruj $N$ losowych próbek w obrębie powierzchni/objętości po czym zsumuj oraz zważ każdy wkład próbki do końcowego wyniku.
Całkowanie Monte Carlo jest obszernym tematem matematycznym i nie będę się dalej zagłębiać w szczegóły, ale wspomnimy, że istnieje również wiele sposobów generowania losowych próbek. Domyślnie każda próbka jest całkowicie (pseudo) losowa, jak jesteśmy do tego przyzwyczajeni, ale wykorzystując pewne właściwości sekwencji pół-losowych, możemy generować wektory próbek, które są nadal losowe, ale mają interesujące właściwości. Na przykład możemy wykonać całkowanie Monte Carlo na czymś, co nazywa się
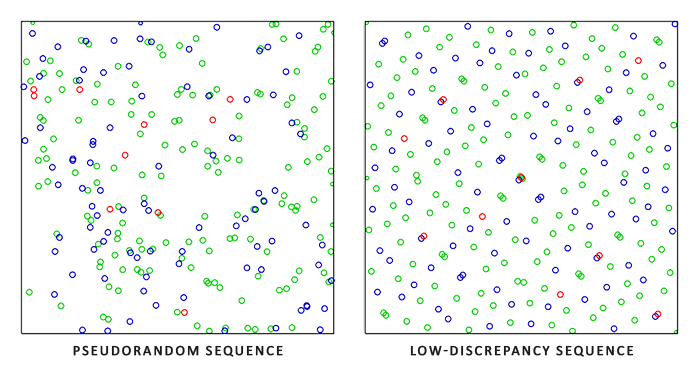
Przy użyciu sekwencji o niskiej rozbieżności do generowania wektorów próbkowania Monte Carlo, proces ten jest znany jako
Biorąc pod uwagę naszą nowo nabytą wiedzę na temat całkowania Monte Carlo i Quasi-Monte Carlo, istnieje interesująca właściwość, którą możemy wykorzystać do uzyskania jeszcze szybszej zbieżności znanej jako
To jest esencja tego jak działa ważność próbkowania: generowanie wektorów próbkowania w niektórych regionach ograniczonych przez chropowatość zorientowaną wokół wektora połowicznego mikrościanki. Łącząc próbkowanie Quasi-Monte Carlo z sekwencją o niskiej rozbieżności i powodowaniu tendencyjności wektorów próbkowania za pomocą ważności próbkowania, uzyskujemy wysoki stopień zbieżności. Ponieważ szybciej docieramy do rozwiązania, potrzebujemy mniej próbek, aby osiągnąć przybliżenie, które jest wystarczające. Dzięki temu, ta kombinacja pozwala nawet aplikacjom graficznym na rozwiązywanie całki zwierciadlanej w czasie rzeczywistym, aczkolwiek wciąż jest to znacznie wolniejsze niż wstępne obliczanie wyników.
Sekwencja o niskiej rozbieżności
W tym samouczku wstępnie obliczymy część lustrzaną równania odbicia pośredniego, korzystając z ważności próbkowania, biorąc pod uwagę losową sekwencję o niskiej rozbieżności w oparciu o metodę Quasi-Monte Carlo. Sekwencja, z której będziemy korzystać, jest określana jako
Biorąc pod uwagę kilka zgrabnych trików, możemy całkiem wydajnie wygenerować sekwencję Van Der Corpus w shaderze, który posłuży nam do uzyskania próbki sekwencji Hammersley’a i dla wszystkich próbek N:
float RadicalInverse_VdC(uint bits)
{
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}
Funkcja
Sekwencja Hammersley bez operatora bitowego
Nie wszystkie sterowniki OpenGL obsługują operatory bitowe (na przykład WebGL i OpenGL ES 2.0). W takim przypadku możesz użyć alternatywnej wersji sekwencji Van Der Corpus, która nie korzysta z operacji bitowych:
float VanDerCorpus(uint n, uint base)
{
float invBase = 1.0 / float(base);
float denom = 1.0;
float result = 0.0;
for(uint i = 0u; i < 32u; ++i)
{
if(n > 0u)
{
denom = mod(float(n), 2.0);
result += denom * invBase;
invBase = invBase / 2.0;
n = uint(float(n) / 2.0);
}
}
return result;
}
// ------------------------------------------------------
vec2 HammersleyNoBitOps(uint i, uint N)
{
return vec2(float(i)/float(N), VanDerCorpus(i, 2u));
}
Zauważ, że ze względu na ograniczenia pętli GLSL na starszym sprzęcie, sekwencja iteruje po wszystkich możliwych 32 bitach. Ta wersja jest mniej wydajna, ale działa na każdym sprzęcie, który nie wspiera operacji bitowych.
Ważność próbkowania GGX
Zamiast jednolitego lub losowego (Monte Carlo) generowania wektorów próbkowania na półkuli całkowania $\Omega$, generujemy wektory próbkowania skierowane w kierunku ogólnej orientacji odbicia mikropowierzchni wektora połowicznego na podstawie chropowatości powierzchni. Proces pobierania próbek będzie podobny do tego, co widzieliśmy wcześniej: rozpoczynamy dużą pętlę, generujemy losową (o niskiej rozbieżności) wartość sekwencji, pobieramy tę wartość sekwencji, aby wygenerować wektor próbkowania w przestrzeni stycznych, przekształcamy ją do przestrzeni świata i próbkujemy radiancję sceny. Różnica polega na tym, że teraz używamy wartości sekwencji o niskiej rozbieżności jako danych wejściowych do wygenerowania wektora próbkowania:
const uint SAMPLE_COUNT = 4096u;
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
Dodatkowo, aby zbudować wektor próbkowania, potrzebujemy jakiegoś sposobu zorientowania i przesunięcia wektora próbkowania w kierunku płata lustrzanego dla pewnej chropowatości powierzchni. Możemy wziąć NDF zgodnie z opisem w tutorialu Teoria PBR i połączyć GGX NDF w procesie sferycznego wektora próbkowania, jak opisało to Epic Games:
vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
{
float a = roughness*roughness;
float phi = 2.0 * PI * Xi.x;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta*cosTheta);
// od współrzędnych sferycznych do współrzędnych kartezjańskich
vec3 H;
H.x = cos(phi) * sinTheta;
H.y = sin(phi) * sinTheta;
H.z = cosTheta;
// od wektora w przestrzeni stycznych do wektora w przestrzeni świata
vec3 up = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
vec3 tangent = normalize(cross(up, N));
vec3 bitangent = cross(N, tangent);
vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
return normalize(sampleVec);
}
Daje nam to wektor próbkowania w pewnym stopniu zorientowany wokół oczekiwanego wektora połówkowego mikropowierzchni na podstawie pewnej szorstkości wejściowej i wartości sekwencji o niskiej rozbieżności Xi. Zauważ, że Epic Games używa chropowatości do kwadratu, aby uzyskać lepsze efekty wizualne, na podstawie oryginalnych badań Disneya dotyczących PBR.
Przy zdefiniowanej sekwencji o niskiej rozbieżności Hammersley’a i generowaniu próbek możemy sfinalizować shader pre-filtrowania:
#version 330 core
out vec4 FragColor;
in vec3 localPos;
uniform samplerCube environmentMap;
uniform float roughness;
const float PI = 3.14159265359;
float RadicalInverse_VdC(uint bits);
vec2 Hammersley(uint i, uint N);
vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness);
void main()
{
vec3 N = normalize(localPos);
vec3 R = N;
vec3 V = R;
const uint SAMPLE_COUNT = 1024u;
float totalWeight = 0.0;
vec3 prefilteredColor = vec3(0.0);
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
vec3 L = normalize(2.0 * dot(V, H) * H - V);
float NdotL = max(dot(N, L), 0.0);
if(NdotL > 0.0)
{
prefilteredColor += texture(environmentMap, L).rgb * NdotL;
totalWeight += NdotL;
}
}
prefilteredColor = prefilteredColor / totalWeight;
FragColor = vec4(prefilteredColor, 1.0);
}
Pre-filtrujemy mapę środowiska, w oparciu o pewną szorstkość wejściową, która zmienia się dla każdego poziomu mipmapy w pre-filtrowanej cubemapie (od 0.0 do 1.0) i zapisuje wynik w prefilteredColor. Wynikowy prefilteredColor jest dzielony przez całkowitą wagę próbki, gdzie próbki o mniejszym wpływie na końcowy wynik (dla małych NdotL) mają mniejszą wagę.
Przechwytywanie pre-filtrowanych poziomów mipmap
Pozostaje tylko pre-filtrować mapę środowiska z różnymi wartościami chropowatości na wielu poziomach mipmap. Jest to dość łatwe do zrobienia dzięki pierwotnej konfiguracji z tutoriala o irradiancji:
prefilterShader.use();
prefilterShader.setInt("environmentMap", 0);
prefilterShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
unsigned int maxMipLevels = 5;
for (unsigned int mip = 0; mip < maxMipLevels; ++mip)
{
// zmień rozmiar bufora ramki zgodnie z rozmiarem mipmapy.
unsigned int mipWidth = 128 * std::pow(0.5, mip);
unsigned int mipHeight = 128 * std::pow(0.5, mip);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, mipWidth, mipHeight);
glViewport(0, 0, mipWidth, mipHeight);
float roughness = (float)mip / (float)(maxMipLevels - 1);
prefilterShader.setFloat("roughness", roughness);
for (unsigned int i = 0; i < 6; ++i)
{
prefilterShader.setMat4("view", captureViews[i]);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,
GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, prefilterMap, mip);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
renderCube();
}
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);
Proces jest podobny do splotu na mapie irradiancji, ale tym razem skalujemy wymiary bufora ramki do odpowiedniego rozmiaru mipmapy, gdzie każdy poziom mipmapy redukuje rozmiar 2-krotnie. Dodatkowo określamy poziom mipmapy, do której renderujemy w ostatnim parametrze
To powinno dać nam odpowiednio pre-filtrowaną mapę środowiska, która zwraca niewyraźne odbicia, im wyższy jest poziom mipmapy, z którego uzyskujemy dostęp. Jeśli wyświetlimy pre-filtrowaną mapę środowiska w shaderze skybox’a i będziemy próbkować nieco powyżej jej pierwszego poziomu mipmapy w shaderze:
vec3 envColor = textureLod(environmentMap, WorldPos, 1.2).rgb;
Otrzymujemy wynik, który rzeczywiście wygląda jak rozmyta wersja oryginalnego środowiska:

Jeśli uzyskałeś nieco podobny wynik, to udało Ci się pre-filtrować mapę środowiska HDR. Pobaw się z różnymi poziomami mipmap, aby zobaczyć, jak mapa pre-filtracji stopniowo zmienia się z ostrych na rozmyte odbicia wraz ze wzrostem poziomów mipmapy.
Artefakty pre-filtracji
Podczas gdy obecna mapa pre-filtracji działa dobrze dla większości celów, prędzej czy później natkniesz się na kilka artefaktów renderowania, które są bezpośrednio związane z konwolucją pre-filtracji. Wymienię najpopularniejsze artefakty tutaj, oraz powiem jak je naprawić.
Szwy (ang. seams) cubemapy dla wysokiej chropowatości
Próbkowanie mapy pre-filtracji na powierzchniach chropowatych oznacza próbkowanie mapy pre-filtracji na niektórych jej niższych poziomach mipmap. Podczas próbkowania cubemap, OpenGL domyślnie nie interpoluje liniowo pomiędzy ściankami cubemapy. Ponieważ niższe poziomy mipmapy mają niższą rozdzielczość, a mapa pre-filtracji jest splatana za pomocą znacznie większego płata próbkowania, brak filtrowania pomiędzy ściankami cubemapy staje się widoczny:

Na szczęście, OpenGL daje nam możliwość prawidłowego filtrowania między ściankami cubemapy poprzez włączenie GL_TEXTURE_CUBE_MAP_SEAMLESS:
glEnable(GL_TEXTURE_CUBE_MAP_SEAMLESS);
Po prostu włącz tę właściwość gdzieś na początku aplikacji, a szwy znikną.
Jasne kropki w mapie pre-filtracji
Ze względu na detale o wysokiej częstotliwości i gwałtownie zmieniające się natężenia światła w odbiciach lustrzanych, konwolucja odbić lustrzanych wymaga dużej liczby próbek, aby odpowiednio uwzględnić zmienny charakter odbić środowiskowych HDR. Pobieramy już bardzo dużą liczbę próbek, ale dla niektórych środowisk może to wciąż nie wystarczać i możesz dostrzec kropki pojawiające się wokół jasnych obszarów:

Jedną z opcji jest zwiększenie liczby próbek, ale to nie wystarczy dla wszystkich środowisk. Zgodnie z opisem Chetan Jags’a możemy zmniejszyć ten artefakt (podczas splotu pre-filtracji) poprzez nie bezpośrednie próbkowanie mapy środowiska, ale próbkowanie z poziomu mipmapy środowiska w oparciu o PDF całki i chropowatość:
float D = DistributionGGX(NdotH, roughness);
float pdf = (D * NdotH / (4.0 * HdotV)) + 0.0001;
float resolution = 512.0; // rozdzielczość źródłowej cubemapy (per ścianka)
float saTexel = 4.0 * PI / (6.0 * resolution * resolution);
float saSample = 1.0 / (float(SAMPLE_COUNT) * pdf + 0.0001);
float mipLevel = roughness == 0.0 ? 0.0 : 0.5 * log2(saSample / saTexel);
Nie zapomnij włączyć filtrowania trójliniowego na mapie środowiska, z której chcesz próbkować mipmapy:
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
I niech OpenGL wygeneruje mipmapy po ustawieniu podstawowej tekstury:
// przekonwertuj mapę środowiskową HDR equirectangular na odpowiednik cubemapy
[...]
// następnie wygeneruj mipmapy
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glGenerateMipmap(GL_TEXTURE_CUBE_MAP);
Działa to zaskakująco dobrze i powinno usunąć większość, jeśli nie wszystkie, kropki w twojej mapie pre-filtracji na chropowatych powierzchniach.
Pre-komputacja BRDF
Z gotowym pre-filtrowanym środowiskiem możemy skoncentrować się na drugiej części aproksymacji rozdzielonych sum: BRDF. Pokrótce przyjrzyjmy się aproksymacji rozdzielonych sum:
\[L_o(p,\omega_o) = \int\limits_{\Omega} L_i(p,\omega_i) d\omega_i * \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i\]Wstępnie obliczyliśmy lewą część aproksymacji rozdzielonych sum na pre-filtrowanej mapie na różnych poziomach chropowatości. Prawa strona wymaga od nas splotu równania BRDF po kącie $n \cdot \omega_o$, chropowatości powierzchni i współczynniku Fresnel’a $F_0$. Jest to podobne do całkowania lustrzanego BRDF ze stałą radiancją $L_i$ równą 1.0. Konwolucja BRDF po 3 zmiennych to trochę dużo, ale możemy przenieść $F_0$ poza równanie BRDF:
Gdzie $F$ jest równaniem Fresnela. Przeniesienie mianownika Fresnela do BRDF daje nam równoważne równanie:
\[\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} F(\omega_o, h) n \cdot \omega_i d\omega_i\]Podstawienie do najbardziej po prawego $F$ przybliżenia Fresnela-Schlicka daje nam:
\[\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0){(1 - \omega_o \cdot h)}^5) n \cdot \omega_i d\omega_i\]Zastąpmy ${(1 - \omega_o \cdot h)}^5$ przez $\alpha$, aby ułatwić rozwiązanie dla $F_0$:
\[\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0)\alpha) n \cdot \omega_i d\omega_i\] \[\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + 1*\alpha - F_0*\alpha) n \cdot \omega_i d\omega_i\] \[\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha) + \alpha) n \cdot \omega_i d\omega_i\]Następnie rozdzielamy funkcję Fresnela $F$ na dwie całki:
\[\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha)) n \cdot \omega_i d\omega_i + \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (\alpha) n \cdot \omega_i d\omega_i\]W ten sposób $F_0$ jest stałą i możemy przenieść $F_0$ poza całkę. Następnie zastępujemy $\alpha$ jej oryginalną formą, dając nam końcowe równanie BRDF:
\[F_0 \int\limits_{\Omega} f_r(p, \omega_i, \omega_o)(1 - {(1 - \omega_o \cdot h)}^5) n \cdot \omega_i d\omega_i + \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) {(1 - \omega_o \cdot h)}^5 n \cdot \omega_i d\omega_i\]Dwie powstałe całki reprezentują odpowiednio skalę i odchylenie dla $F_0$. Zauważ, że ponieważ $f(p, \omega_i, \omega_o)$ zawiera już termin $F$, oba się znoszą, usuwając $F$ z $f$.
W podobny sposób do wcześniejszej splecionej mapy środowiska, możemy spleść równania BRDF na ich danych wejściowych: kąt pomiędzy $n$ a $\omega_o$ i chropowatość, i przechowywać splecione wyniki w teksturze. Przechowujemy splecione wyniki w postaci tekstury 2D (LUT) znanej jako mapa
Shader konwolucji BRDF działa na płaszczyźnie 2D, używając współrzędnych tekstury 2D bezpośrednio jako danych wejściowych do splotu BRDF (NdotV i roughness). Kod splotu jest w dużym stopniu podobny do splotu pre-filtracji, z tą różnicą, że przetwarza teraz wektor próbkowania zgodnie z funkcją geometrii BRDF i aproksymacją Fresnela-Schlicka:
vec2 IntegrateBRDF(float NdotV, float roughness)
{
vec3 V;
V.x = sqrt(1.0 - NdotV*NdotV);
V.y = 0.0;
V.z = NdotV;
float A = 0.0;
float B = 0.0;
vec3 N = vec3(0.0, 0.0, 1.0);
const uint SAMPLE_COUNT = 1024u;
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
vec3 L = normalize(2.0 * dot(V, H) * H - V);
float NdotL = max(L.z, 0.0);
float NdotH = max(H.z, 0.0);
float VdotH = max(dot(V, H), 0.0);
if(NdotL > 0.0)
{
float G = GeometrySmith(N, V, L, roughness);
float G_Vis = (G * VdotH) / (NdotH * NdotV);
float Fc = pow(1.0 - VdotH, 5.0);
A += (1.0 - Fc) * G_Vis;
B += Fc * G_Vis;
}
}
A /= float(SAMPLE_COUNT);
B /= float(SAMPLE_COUNT);
return vec2(A, B);
}
// ----------------------------------------------------------------------------
void main()
{
vec2 integratedBRDF = IntegrateBRDF(TexCoords.x, TexCoords.y);
FragColor = integratedBRDF;
}
Jak widać, splot BRDF jest bezpośrednim tłumaczeniem matematyki na kod. Bierzemy zarówno kąt $\theta$, jak i chropowatość jako dane wejściowe, generujemy wektor próbkowania biorąc pod uwagę ważność próbkowania, przetwarzamy go względem geometrii i terminu BRDF Fresnela i wyprowadzamy zarówno skalę, jak i odchylenie $F_0$ dla każdej próbki, uśredniając wyniki na końcu.
Być może przypominasz sobie z tutoriala Teoria PBR, że termin geometrii BRDF jest nieco inny, gdy używa się go razem z IBL, ponieważ jego zmienna $k$ ma nieco inną interpretację:
\[k_{direct} = \frac{(\alpha + 1)^2}{8}\] \[k_{IBL} = \frac{\alpha^2}{2}\]Ponieważ splot BRDF jest częścią zwierciadlanej całki IBL, użyjemy $k_{IBL}$ dla funkcji geometrii Schlick’a-GGX:
float GeometrySchlickGGX(float NdotV, float roughness)
{
float a = roughness;
float k = (a * a) / 2.0;
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
// ----------------------------------------------------------
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx2 = GeometrySchlickGGX(NdotV, roughness);
float ggx1 = GeometrySchlickGGX(NdotL, roughness);
return ggx1 * ggx2;
}
Zauważ, że podczas gdy $k$ przyjmuje a jako swój parametr, nie podnieśliśmy do kwadratu roughness jako zmiennej a tak, jak pierwotnie robiliśmy dla innych interpretacji a; prawdopodobnie dlatego, że a jest już podniesione do kwadratu. Nie jestem pewien, czy jest to niezgodność ze strony Epic Games, czy oryginalnego artykułu Disneya, ale bezpośrednie przełożenie roughness na a daje mapę integracji BRDF, która jest identyczna z wersją Epic Games.
Na koniec, aby zapisać wynik splotu BRDF, wygenerujemy teksturę 2D o rozdzielczości 512 na 512.
unsigned int brdfLUTTexture;
glGenTextures(1, &brdfLUTTexture);
// wstępnie przydziel wystarczającą ilość pamięci dla tekstury LUT.
glBindTexture(GL_TEXTURE_2D, brdfLUTTexture);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RG16F, 512, 512, 0, GL_RG, GL_FLOAT, 0);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
Zwróć uwagę, że używamy precyzji 16-bitowej typu float zalecanego przez Epic Games. Pamiętaj, aby ustawić tryb zawijania na GL_CLAMP_TO_EDGE, aby zapobiec artefaktom próbkowania krawędzi.
Następnie ponownie użyjemy tego samego obiektu bufora ramki i uruchomimy ten shader kwadracie całoekranowym:
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, brdfLUTTexture, 0);
glViewport(0, 0, 512, 512);
brdfShader.use();
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
RenderQuad();
glBindFramebuffer(GL_FRAMEBUFFER, 0);
Spleciona część BRDF rozdzielonych sum powinna dać następujący wynik:

Zarówno z pre-filtrowaną mapa środowiska, jak i teksturą BRDF 2D LUT, możemy ponownie zbudować pośrednią całkę zwierciadlaną zgodnie z aproksymacją rozdzielonych sum. Połączony wynik działa wówczas jako pośrednie lub ambientowe światło zwierciadlane.
Uzupełnienie współczynnika odbicia IBL
Aby uzyskać pośrednią część lustrzaną równania odbicia, musimy połączyć ze sobą obie części przybliżenia rozdzielonych sum. Zacznijmy od dodania wstępnie obliczonych danych o oświetleniu do górnej części naszego shadera PBR:
uniform samplerCube prefilterMap;
uniform sampler2D brdfLUT;
Najpierw otrzymujemy pośrednie odbicia lustrzane powierzchni poprzez próbkowanie pre-filtrowanej mapy środowiska za pomocą wektora odbicia. Zwróć uwagę, że próbkujemy odpowiedni poziom mipmapy w oparciu o chropowatość powierzchni, dając bardziej chropowatym powierzchniom bardziej rozmyte odbicia lustrzane.
void main()
{
[...]
vec3 R = reflect(-V, N);
const float MAX_REFLECTION_LOD = 4.0;
vec3 prefilteredColor = textureLod(prefilterMap, R, roughness * MAX_REFLECTION_LOD).rgb;
[...]
}
W etapie pre-filtrowania spletliśmy mapę środowiska maksymalnie do 5 poziomów mipmapy (0 do 4), co oznaczamy tutaj jako MAX_REFLECTION_LOD, aby upewnić się, że nie próbkujemy poziomu mipmapy, na której nie ma (odpowiednich) danych.
Następnie próbkujemy z tekstury całkowania BRDF, biorąc pod uwagę chropowatość materiału i kąt między wektorem normalnym a wektorem patrzenia:
vec3 F = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);
vec2 envBRDF = texture(brdfLUT, vec2(max(dot(N, V), 0.0), roughness)).rg;
vec3 specular = prefilteredColor * (F * envBRDF.x + envBRDF.y);
Biorąc pod uwagę skalę i odchylenie $F_0$ (tutaj bezpośrednio używamy pośredniego wyniku Fresnela F) z tekstury BRDF, łączymy to z lewą częścią równania pre-filtracji odbicia IBL i ponownie tworzymy przybliżony wynik całkowy jako specular.
Daje nam to pośrednią lustrzaną część równania odbicia. Teraz połączymy to z rozproszoną częścią równania współczynnika odbicia z ostatniego tutoriala i otrzymujemy pełny wynik IBL PBR:
vec3 F = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);
vec3 kS = F;
vec3 kD = 1.0 - kS;
kD *= 1.0 - metallic;
vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse = irradiance * albedo;
const float MAX_REFLECTION_LOD = 4.0;
vec3 prefilteredColor = textureLod(prefilterMap, R, roughness * MAX_REFLECTION_LOD).rgb;
vec2 envBRDF = texture(brdfLUT, vec2(max(dot(N, V), 0.0), roughness)).rg;
vec3 specular = prefilteredColor * (F * envBRDF.x + envBRDF.y);
vec3 ambient = (kD * diffuse + specular) * ao;
Zwróć uwagę, że nie mnożymy specular z kS, ponieważ mamy tam już mnożenie z Fresnela.
Teraz, uruchamiając ten kod w scenie z serią kulek, które różnią się szorstkością i właściwościami metalicznymi, w końcu widzimy ich prawdziwe kolory w ostatecznym renderze PBR:

Moglibyśmy nawet zaszaleć i użyć fajnych tekstur materiałów PBR:

Lub załadować ten niesamowity darmowy model 3D PBR autorstwa Andrew Maximov:

Jestem pewien, że wszyscy możemy się zgodzić, że nasze oświetlenie wygląda teraz o wiele bardziej przekonująco. Co jest jeszcze lepsze, nasze oświetlenie wygląda fizycznie poprawnie, niezależnie od używanej mapy środowiska. Poniżej przedstawiam kilka różnych wstępnie obliczonych map HDR, całkowicie zmieniających dynamikę oświetlenia, ale wciąż wyglądających fizycznie poprawnie bez zmiany pojedynczej zmiennej oświetlenia!

Ta przygoda z PBR okazała się dość długa. Jest wiele kroków, a zatem wiele może się nie udać, więc ostrożnie porównaj swoją pracę z kodem sceny kulek lub oteksturowanej sceny (w tym porównaj wszystkie shadery), jeśli utknąłeś, lub sprawdź i zapytaj w komentarzach.
Co dalej?
Mamy nadzieję, że na tym etapie tego samouczka powinieneś mieć dość jasne zrozumienie, czym jest PBR, a nawet mieć rzeczywisty renderer PBR. W tych samouczkach wstępnie obliczyliśmy wszystkie odpowiednie dane oświetlenia oparte na obrazie PBR na początku naszej aplikacji, przed pętlą renderowania. To było dobre dla celów edukacyjnych, ale niezbyt dobre do praktycznego wykorzystania PBR. Po pierwsze, obliczenia wstępne muszą być wykonane tylko raz, a nie przy każdym starcie. Po drugie, w momencie, gdy korzystasz z wielu map środowiska, będziesz musiał wstępnie obliczyć każdą z nich przy każdym starcie aplikacji.
Z tego powodu na ogół wstępnie obliczasz mapę środowiska do mapy irradiancji i pre-filtrujesz mapę tylko raz, a następnie przechowujesz ją na dysku (pamiętaj, że mapa całkowania BRDF nie jest zależna od mapy środowiska, więc potrzebujesz tylko obliczyć lub załadować ją tylko raz). Oznacza to, że musisz wymyślić niestandardowy format obrazu, aby przechowywać cubemapy HDR, w tym poziomy mipmap. Możesz też przechowywać (i ładować) go jako jeden z dostępnych formatów (np. .dds, który obsługuje przechowywanie poziomów mipmap).
Ponadto opisaliśmy cały proces w tych samouczkach, w tym generowanie wstępnie obliczonych obrazów IBL, aby pomóc nam lepiej zrozumieć przebieg PBR. Ale będziesz równie dobrze, jeżeli użyjesz kilku świetnych narzędzi, takich jak cmftStudio lub IBLBaker, które mogą wygenerować te wstępnie obliczone mapy za ciebie.
Jeden punkt, który pominęliśmy, to wstępnie obliczone cubemapy jako
Więcej informacji
- Real Shading in Unreal Engine 4: wyjaśnia aproksymację rozdzielonych sum autorstwa Epic Games. Jest to artykuł, na którym oparty jest kod IBL PBR.
- Physically Based Shading and Image Based Lighting: świetny post na blogu Trenta Reeda na temat całkowania części specular IBL w PBR w czasie rzeczywistym.
- Image Based Lighting: bardzo obszerny artykuł Chetan Jags’a o odbiciach lustrzanych opartych na obrazie i kilku jego zastrzeżeniach, w tym interpolacja sond odbić.
- Moving Frostbite to PBR: Szczegółowy opis integracji PBR z silnikiem gry AAA autorstwa Sébastiena Lagarde’a i Charlesa de Rousiersa.
- Physically Based Rendering – Part Three: przegląd oświetlenia IBL i PBR przez zespół JMonkeyEngine.
- Implementation Notes: Runtime Environment Map Filtering for Image Based Lighting: obszerny artykuł Padraic Hennessy’a o pre-filtrowaniu map środowiska HDR i znaczącej optymalizacji procesu próbkowania.