This is the Polish translation of Advanced-Lighting/Gamma-Correction article of learnopengl.com tutorial series.

Jak tylko obliczyliśmy wszystkie końcowe kolory pikseli sceny, będziemy musieli wyświetlić je na monitorze. W dawnych czasach obrazowania cyfrowego większość monitorów to były monitory kineskopowe (CRT). Monitory te miały fizyczną właściwość, że dwukrotność napięcia wejściowego nie powodowało dwukrotnej jasności. Podwojenie napięcia wejściowego doprowadziło do uzyskania jasności równej wykładniczej zależności wynoszącej w przybliżeniu 2.2, znanej również jako gamma monitora. Również (przypadkowo) tak samo ludzie mierzą jasność, ponieważ jasność jest również wyświetlana z podobną (odwrotną) relacją mocy. Aby lepiej zrozumieć, co to oznacza, spójrz na następującą ilustrację:

Liniowe kodowanie wyświetlacza z korekcją gamma i bez niej

Górna linia wygląda jak poprawna skala jasności dla ludzkiego oka, podwajając jasność (na przykład od 0.1 do 0.2) rzeczywiście wygląda tak, jakby była dwa razy jaśniejsza z ładnymi stałymi różnicami. Jednak, gdy mówimy o fizycznej jasności światła, np. ilość fotonów opuszczających źródło światła, dolna skala faktycznie wyświetla prawidłową jasność. W dolnej skali podwojenie jasności zwraca prawidłową jasność fizyczną, ale ponieważ nasze oczy inaczej postrzegają jasność (bardziej podatne na zmiany w ciemnych kolorach), wygląda to dziwnie.

Ponieważ ludzkie oczy wolą widzieć kolory jasności zgodnie z górną skalą, monitory (do dziś) wykorzystują zależność mocy do wyświetlania kolorów wyjściowych, aby oryginalne fizyczne kolory jasności były odwzorowane na nieliniowe kolory jasności w górnej skali; w zasadzie dlatego, że wygląda to lepiej.

To nieliniowe odwzorowanie monitorów rzeczywiście sprawia, że ​​jasność wygląda lepiej w naszych oczach, ale jeśli chodzi o renderowanie grafiki, jest jeden problem: wszystkie kolory i ich jasności, które konfigurujemy w naszych aplikacjach, opierają się na tym, co odbieramy z monitora a zatem wszystkie opcje są faktycznie nieliniowymi opcjami jasności/koloru. Spójrz na poniższy wykres:

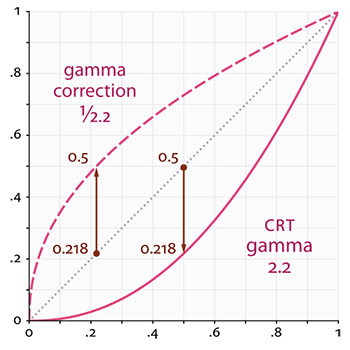
Krzywe gamma

Linia kropkowana przedstawia wartości koloru/światła w przestrzeni liniowej, a linia ciągła reprezentuje przestrzeń barw, którą wyświetla monitor. Jeśli podwoimy kolor w przestrzeni liniowej, jego wynik jest rzeczywiście podwojony. Na przykład, weź wektor barwy światła $\bar{L} = (0.5, 0.0, 0.0)$, który reprezentuje pół-ciemne czerwone światło. Gdybyśmy podwoili to światło w przestrzeni liniowej, dałoby to w wyniku $(1.0, 0.0, 0.0)$, jak widać na wykresie. Ponieważ jednak zdefiniowane przez nas kolory muszą nadal wyświetlać się na monitorze, kolor zostanie wyświetlony na monitorze w postaci $(0.218, 0.0, 0.0)$, jak widać na wykresie. Oto, gdzie zaczynają się pojawiać problemy: kiedy podwoimy ciemnoczerwone światło w liniowej przestrzeni, w rzeczywistości staje się ono prawie 2.5 razy ciemniejsze na monitorze!

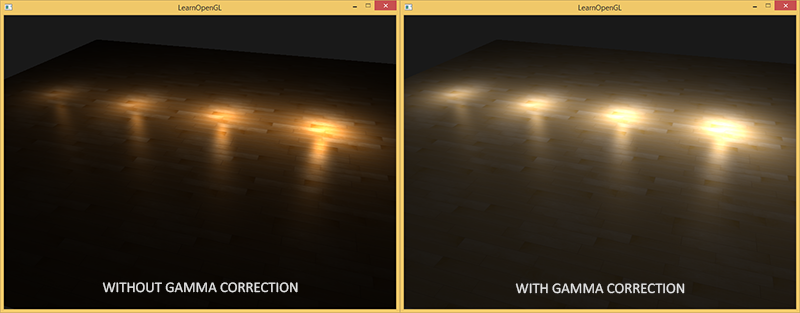
Ponieważ kolory są konfigurowane w oparciu o wyświetlacz monitora, wszystkie obliczenia pośrednie (oświetlenie) w przestrzeni liniowej są niepoprawne fizycznie. Staje się to coraz bardziej oczywiste, ponieważ używa się bardziej zaawansowanych algorytmów oświetleniowych, co widać na poniższym obrazku:

Przykład z i bez korekcji gamma w trybie zaawansowanym

Widać, że z korekcją gamma (zaktualizowane) wartości kolorów działają przyjemniej razem, a ciemniejsze obszary są mniej ciemne, a więc pokazują więcej szczegółów. Ogólnie rzecz biorąc, znacznie uzyskujemy lepszą jakość obrazu przy niewielkich modyfikacjach.

Bez właściwego korygowania gammy monitora oświetlenie wygląda źle, a artyści będą mieli problemy z uzyskaniem realistycznych i dobrze wyglądających wyników. Rozwiązaniem jest zastosowanie korekcji gamma.

Korekcja gamma

Ideą korekcji gamma jest zastosowanie odwrotności gammy monitora do końcowego koloru wyjściowego przed wyświetleniem na monitorze. Patrząc wstecz na poprzedni wykres krzywej gamma, widzimy kolejną przerywaną linię, która jest odwrotnością krzywej gamma monitora. Mnożymy każdy z liniowych kolorów wyjściowych za pomocą tej odwrotnej krzywej gamma (dzięki czemu kolory stają się jaśniejsze) i gdy tylko kolory są wyświetlane na monitorze, krzywa gamma monitora zostaje zastosowana, a uzyskane kolory stają się liniowe. Zasadniczo sprawiamy, że kolory pośrednie są jaśniejsze, więc gdy monitor je przyciemnia, to wszystko jest wyrównywane.

Podajmy inny przykład. Powiedzmy, że znowu mamy ciemno-czerwony kolor $(0.5, 0.0, 0.0)$. Przed wyświetleniem tego koloru na monitorze najpierw zastosujemy krzywą korekcji gamma do wartości koloru. Liniowe kolory wyświetlane przez monitor są z grubsza skalowane za pomocą wykładnika $2.2$, więc odwrotność wymaga skalowania kolorów o wykładniku $1/2.2$. Skorygowany kolor ciemnoczerwony staje się zatem $(0.5, 0.0, 0.0)^{1/2.2} = (0.5, 0.0, 0.0)^{0.45} = (0.73, 0.0, 0.0)$. Skorygowane kolory są następnie podawane do monitora, w wyniku czego kolor jest wyświetlany jako $(0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)$. Widać, że za pomocą korekcji gamma monitor nareszcie wyświetla kolory, tak jak je ustawiamy w aplikacji.

Wartość gamma 2.2 jest domyślną wartością gamma, która z grubsza szacuje średnią gamma większości monitorów. Przestrzeń barw w wyniku tej gammy 2.2 nazywana jest przestrzenią kolorów sRGB. Każdy monitor ma własne krzywe gamma, ale wartość gamma równa 2.2 daje dobre wyniki na większości monitorów. Z tego powodu gry często pozwalają graczom zmieniać ustawienia gamma gry, ponieważ może się nieznacznie różnić w zależności od monitora.

Istnieją dwa sposoby zastosowania korekcji gamma do scen:

  • Korzystając z wbudowanej obsługi framebuffer’ów sRGB w OpenGL.
  • Lub robiąc korektę gamma samemu w Fragment Shader.

Pierwsza opcja jest prawdopodobnie najłatwiejsza, ale daje też mniej kontroli. Włączając GL_FRAMEBUFFER_SRGB, mówisz OpenGL, że każde kolejne polecenie rysowania powinno najpierw poprawić gammę kolorów z przestrzeni kolorów sRGB przed zapisaniem ich w buforach kolorów. sRGB jest przestrzenią barw, która z grubsza odpowiada gammie 2.2 i jest standardem dla większości domowych urządzeń. Po włączeniu GL_FRAMEBUFFER_SRGB OpenGL automatycznie wykona korekcję gamma po uruchomieniu każdego Fragment Shadera do wszystkich kolejnych buforów ramki, w tym domyślnego framebuffera.

Włączenie GL_FRAMEBUFFER_SRGB jest tak proste jak wywołanie glEnable:

    glEnable(GL_FRAMEBUFFER_SRGB);

Odtąd renderowane obrazy będą poddawane korekcji gamma, a ponieważ jest to robione przez sprzęt, jest całkowicie darmowe. Należy pamiętać o tym podejściu (i innym podejściu), że korekcja gamma (także) przekształca kolory z przestrzeni liniowej w przestrzeń nieliniową, dlatego bardzo ważne jest, aby dokonać korekty gamma tylko na ostatnim etapie. Jeśli zastosujesz korekcję gamma przed końcowym wynikiem, wszystkie kolejne operacje na tych kolorach będą działać na nieprawidłowych wartościach. Na przykład, jeśli korzystasz z wielu buforów ramek, prawdopodobnie chcesz, aby pośrednie wyniki były przekazywane między buforami ramek w przestrzeni liniowej i tylko ostatni framebuffer stosuje korektę gamma przed wysłaniem wartości do monitora.

Drugie podejście wymaga nieco więcej pracy, ale daje nam również pełną kontrolę nad operacjami gamma. Stosujemy korektę gamma na końcu każdego Fragment Shadera, aby ostateczne kolory miały poprawioną gammę przed wysłaniem ich do monitora:

    void main()
    {
        // Zrób super oświetlenie
        [...]
        // zastosuj korekcję gamma
        float gamma = 2.2;
        FragColor.rgb = pow(fragColor.rgb, vec3(1.0/gamma));
    }

Ostatnia linijka kodu podnosi każdy poszczególny komponent koloru fragColor do potęgi 1.0/gamma poprawiając kolor wyjściowy tego fragmentu.

Problem z tym podejściem polega na tym, że aby zachować spójność, musisz zastosować korektę gamma do każdego Fragment Shadera, który przyczynia się do końcowego wyniku, więc jeśli masz kilkanaście Fragment Shaderów dla wielu obiektów, musisz dodać kod korekcji gamma do każdego z nich. Łatwiejszym rozwiązaniem byłoby wprowadzenie etapu post-processingu w pętli renderowania i zastosowanie korekcji gamma na kwadracie pełnoekranowym jako ostatni krok, który wystarczy zrobić tylko raz.

Ta jedna linijka kodu stanowi techniczną implementację korekcji gamma. Nie jest to zbyt imponujące, ale przy korekcji gamma trzeba wziąć pod uwagę kilka dodatkowych rzeczy.

Tekstury sRGB

Ponieważ monitory zawsze wyświetlają kolory z zastosowaną gammą w przestrzeni sRGB, za każdym razem, gdy rysujesz, edytujesz lub malujesz obraz na swoim komputerze, wybierasz kolory w zależności od tego, co widzisz na monitorze. Oznacza to, że wszystkie utworzone lub edytowane obrazy nie znajdują się w przestrzeni liniowej, ale w przestrzeni sRGB, np. podwojenie ciemno-czerwonego koloru na ekranie w oparciu o postrzeganą jasność, nie równa się podwójnemu czerwonemu komponentowi.

W rezultacie, artyści tworzą wszystkie tekstury w przestrzeni sRGB, więc jeśli użyjemy tych tekstur, ponieważ korzystamy z nich w naszej aplikacji, musimy wziąć to pod uwagę. Zanim zastosowaliśmy korekcję gamma, nie było to problemem, ponieważ tekstury wyglądały dobrze w przestrzeni sRGB i bez korekcji gamma pracowaliśmy również w przestrzeni sRGB, więc tekstury były wyświetlane dobrze. Jednak teraz, gdy wyświetlamy wszystko w przestrzeni liniowej, kolory tekstury będą złe, jak pokazuje to poniższy obraz:

Porównanie pracy w przestrzeni liniowej z teksturami sRGB i teksturami w przestrzeni liniowej

Obrazy tekstury są zbyt jasne i dzieje się tak, ponieważ gamma jest dwukrotnie poprawiana! Pomyśl o tym, kiedy tworzymy obraz w oparciu o to, co widzimy na monitorze, skutecznie dopasowujemy wartości gamma kolorów obrazu tak, aby wyglądał dokładnie tak samo na monitorze. Ponieważ kiedy ponownie poprawiamy gammę w rendererze, obrazy będą zbyt jasne.

Aby rozwiązać ten problem, musimy upewnić się, że artyści pracują w przestrzeni liniowej. Ponieważ jednak większość twórców tekstur nawet nie wie, czym jest korekcja gamma i łatwiej jest pracować w przestrzeni sRGB, prawdopodobnie nie jest to preferowane rozwiązanie.

Drugim rozwiązaniem jest ponowne poprawienie lub przekształcenie tych tekstur sRGB z powrotem do przestrzeni liniowej przed wykonaniem jakichkolwiek obliczeń ich wartości kolorów. Możemy to zrobić w następujący sposób:

    float gamma = 2.2;
    vec3 diffuseColor = pow(texture(diffuse, texCoords).rgb, vec3(gamma));

Zrobienie tego dla każdej tekstury w przestrzeni sRGB jest dość kłopotliwe. Na szczęście OpenGL daje nam jeszcze inne rozwiązanie naszych problemów, dając nam wewnętrzne formaty tekstur GL_SRGB i GL_SRGB_ALPHA.

Jeśli tworzymy teksturę w OpenGL z dowolnym z tych dwóch formatów tekstur sRGB, OpenGL automatycznie skoryguje kolory do przestrzeni liniowej, gdy tylko ich użyjemy, co pozwoli nam właściwie pracować w przestrzeni liniowej z wszystkimi wyodrębnionymi wartościami kolorów. Możemy określić teksturę jako teksturę sRGB w następujący sposób:

    glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);

Jeśli chcesz dodać elementy alfa do swojej tekstury, musisz określić wewnętrzny format tekstury jako GL_SRGB_ALPHA.

Należy zachować ostrożność podczas określania tekstur w przestrzeni sRGB, ponieważ nie wszystkie tekstury będą w rzeczywistości w przestrzeni sRGB. Tekstury używane do kolorowania obiektów takich jak tekstury diffuse prawie zawsze znajdują się w przestrzeni sRGB. Tekstury używane do wyszukiwania parametrów oświetlenia, takich jak mapy specular i mapy normalnych są prawie zawsze w przestrzeni liniowej, więc gdybyś skonfigurował je również jako tekstury sRGB, oświetlenie się zepsuje. Uważaj, które tekstury określasz jako sRGB.

Dzięki naszym teksturom diffuse określonym jako tekstury sRGB otrzymujesz efekt wizualny, którego oczekujesz, ale tym razem wszystko jest korygowane tylko raz.

Tłumienie (ang. attenuation)

Kolejną rzeczą, która będzie inna przy korekcji gamma, jest tłumienie oświetlenia. W prawdziwym świecie oświetlenie jest delikatnie tłumione odwrotnie proporcjonalnie do kwadratu odległości od źródła światła. W normalnym języku oznacza to po prostu, że natężenie światła zmniejsza się wraz z kwadratem odległości od źródła światła, jak widać to poniżej:

    float attenuation = 1.0 / (distance * distance);

Jednak przy stosowaniu tego równania tłumienia efekt tłumienia jest zawsze zbyt silny, dając światło o małym promieniu, który nie wygląda fizycznie poprawnie. Z tego powodu użyto innych funkcji tłumienia, jak omówiliśmy to w tutorialach podstawy oświetlenia, które dają o wiele więcej kontroli, lub używa się liniowego równania:

    float attenuation = 1.0 / distance;

Liniowe równanie daje znacznie bardziej wiarygodne wyniki niż jego kwadratowy wariant bez korekcji gamma, ale gdy włączymy korekcję gamma, tłumienie liniowe wygląda na zbyt słabe, a poprawne fizycznie tłumienie kwadratowe nagle daje lepsze wyniki. Poniższy obrazek pokazuje różnice:

Różnice tłumienia między korygowaną i nieskorygowaną gammą sceny.

Przyczyną tej różnicy jest to, że funkcje tłumienia światła zmieniają jasność, a ponieważ nie wizualizowaliśmy naszej sceny w przestrzeni liniowej, wybraliśmy funkcje tłumienia, które wyglądały najlepiej na naszym monitorze, ale nie były poprawne fizycznie. Pomyśl o kwadratowej funkcji tłumienia, jeśli użyjemy tej funkcji bez korekcji gamma, efektywnie funkcja tłumienia staje się: $(1.0 / distance^2)^{2.2}$, gdy wyświetlana jest na monitorze. Stwarza to znacznie większy efekt tłumienia bez korekcji gamma. Wyjaśnia to również, dlaczego ekwiwalent liniowy ma dużo więcej sensu bez korekcji gamma, ponieważ daje to $(1.0 / distance)^{2.2} = 1.0 / distance^{2.2}$, który przypomina znacznie jego fizyczny odpowiednik.

Bardziej zaawansowana funkcja tłumienia omówiona w podstawach oświetlenia jest nadal przydatna w scenach z korektą gamma, ponieważ zapewnia znacznie większą kontrolę nad dokładnym tłumieniem (ale oczywiście wymaga innych parametrów w scenie z korekcją gamma).

Stworzyłem prostą scenę demo, której kod źródłowy można znaleźć tutaj. Naciskając klawisz spacji, przełączamy się między sceną z poprawioną gammą na scenę z nieskorygowaną gammą, przy czym obie sceny używają odpowiednich tekstur i funkcji tłumienia. To nie jest najbardziej imponujące demo, ale pokazuje jak właściwie zastosować wszystkie techniki.

Podsumowując, korekcja gamma pozwala ci wizualizować swoje rendery w przestrzeni liniowej. Ponieważ przestrzeń liniowa ma sens w świecie fizycznym, większość fizycznych równań daje obecnie dobre wyniki, takie jak prawdziwe tłumienie światła. Im bardziej zaawansowane staje się oświetlenie, tym łatwiej uzyskać dobre (i realistyczne) wyniki dzięki korekcji gamma. Z tego powodu zaleca się modyfikowanie parametrów oświetlenia tylko po wprowadzeniu korekcji gamma.

Dodatkowe zasoby