This is the Polish translation of Advanced-Lighting/Shadows/Point-Shadows article of learnopengl.com tutorial series.
W ostatnim tutorialu nauczyliśmy się tworzyć dynamiczne cienie za pomocą shadow mappingu. Działa to świetnie, ale nadaje się tylko dla kierunkowych świateł, ponieważ cienie są generowane tylko w jednym kierunku źródła światła. Dlatego jest to również znane jako
Na czym skupi się ten samouczek, to generowanie dynamicznych cieni we wszystkich otaczających kierunkach. Technika, której używamy, jest idealna dla świateł punktowych, ponieważ prawdziwe światło punktowe rzucałoby cienie we wszystkich kierunkach. Ta technika znana jest jako cienie punktowych świateł lub bardziej formalnie jako
Ten samouczek opiera się na poprzednim tutorialu, więc jeśli nie znasz tradycyjnego shadow mappingu, zaleca się przeczytanie najpierw poprzedniego samouczka.
Algorytm pozostaje w większości taki sam jak dla kierunkowego źródła światła: generujemy mapę głębokości z perspektywy światła, próbkujemy mapę głębokości na podstawie aktualnej pozycji fragmentu i porównujemy każdy fragment z zapisaną wartością głębokości, aby zobaczyć, czy jest on w cieniu. Główną różnicą między mapowaniem cieni dla punktowych źródeł światła a mapowaniem cieni dla kierunkowych świateł jest map głębokości.
Potrzebna nam mapa głębi wymaga renderowania sceny ze wszystkich otaczających kierunków światła punktowego i jako taka normalna mapa głębi 2D nie będzie działać; co jeśli zamiast tego użyjemy cubemapy? Ponieważ cubemapa może przechowywać dane środowiskowe z 6 powierzchniami, można wyrenderować całą scenę do każdej z powierzchni mapy w kształcie sześcianu i próbkować ją jako otaczające wartości głębokości światła punktowego.
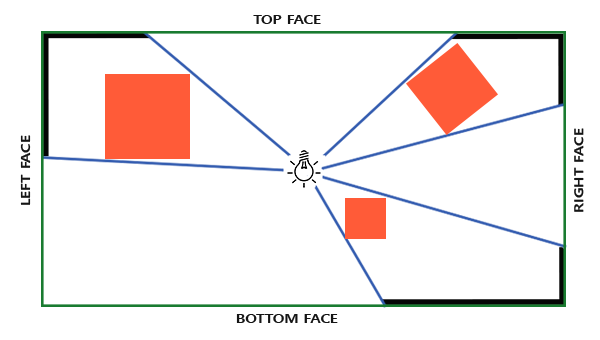
Wygenerowana cubemapa głębokości jest następnie przekazywana do shadera oświetlenia, który pobiera próbkę cubemapy za pomocą wektora kierunkowego, aby pobrać głębię (z perspektywy światła) dla tego fragmentu. Większość skomplikowanych rzeczy omówiliśmy już w poprzednim samouczku o shadow mappingu. Tym, co czyni ten algorytm nieco trudniejszym, jest generowanie cubemapy głębokości.
Generowanie cubemapy głębokości
Aby utworzyć cubemapę głębokości otoczenia światła, musimy renderować scenę 6 razy: raz dla każdej ścianki. Jednym (dość oczywistym) sposobem na zrobienie tego jest renderowanie sceny 6 razy z 6 różnymi macierzami widoku, za każdym razem dołączając inną ściankę do obiektu bufora ramki. Wyglądałoby to mniej więcej tak:
for(unsigned int i = 0; i < 6; i++)
{
GLenum face = GL_TEXTURE_CUBE_MAP_POSITIVE_X + i;
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, face, depthCubemap, 0);
BindViewMatrix(lightViewMatrices[i]);
RenderScene();
}
Może to być dość kosztowne, ponieważ wiele wywołań renderowania jest potrzebnych tylko dla jednej mapy głębokości. W tym samouczku zastosujemy alternatywne (bardziej zorganizowane) podejście, wykorzystując małą sztuczkę w Geometry Shader, która pozwala nam zbudować cubemapę głębokości podczas jednego wywołania rysowania (ang. draw call).
Najpierw musimy utworzyć cubemapę:
unsigned int depthCubemap;
glGenTextures(1, &depthCubemap);
I wygenerować każdą z pojedynczych ścianek cubemapy jako obrazy głębokości 2D:
const unsigned int SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
for (unsigned int i = 0; i < 6; ++i)
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_DEPTH_COMPONENT,
SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);
Nie zapomnij również ustawić odpowiednich parametrów tekstury:
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
Normalnie do obiektu bufora ramki zostałaby dołączona pojedyncza ścianka cubemapy jako tekstura dla framebuffer’a i 6-krotnie wyrenderowana scena, za każdym razem przełączając bufor głębi bufora ramki na inną ściankę cubemapy. Ponieważ zamierzamy użyć Geometry Shadera, który pozwala nam renderować do wszystkich ścianek na raz w jednym przebiegu renderowania, możemy bezpośrednio dołączyć cubemapę jako załącznik głębokości bufora ramki za pomocą
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthCubemap, 0);
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
Ponownie wywołujemy
Przy mapach cieni świateł punktowych mamy dwa przebiegi renderowania: najpierw generujemy mapę głębi, a potem używamy tej mapy głębokości, aby tworzyć cienie w scenie. W przypadku obiektu framebuffer i cubemapy ten proces wygląda trochę tak:
// 1. wygeneruj mapę głębokości
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glClear(GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
RenderScene();
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 2. normalnie wyrenderuj scenę korzystając z mapy głębokości (cubemap)
glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
RenderScene();
Proces jest dokładnie taki sam, jak w przypadku wcześniejszego shadow mappingu, chociaż tym razem renderujemy i używamy cubemap głębokości w porównaniu do tekstury głębi 2D. Zanim wyrenderujemy scenę ze wszystkich kierunków światła, musimy najpierw obliczyć odpowiednie macierze transformacji.
Transformacje przestrzeni światła
Po ustawieniu framebuffera i cubemapy potrzebujemy jakiegoś sposobu, aby przekształcić całą geometrię sceny w odpowiednie przestrzenie światła we wszystkich 6 kierunkach światła. Podobnie do tutoriala shadow mapping potrzebujemy macierzy transformacji światła $T$, ale tym razem po jednej na każdą ściankę cubemapy.
Każda macierz transformacji przestrzeni światła zawiera zarówno macierz projekcji, jak i widoku. Do macierzy projekcji wykorzystamy macierz rzutowania perspektywicznego; źródło światła reprezentuje punkt w przestrzeni, więc rzut perspektywiczny ma największy sens. Każda macierz transformacji przestrzeni światła używa tej samej macierzy projekcji:
float aspect = (float)SHADOW_WIDTH/(float)SHADOW_HEIGHT;
float near = 1.0f;
float far = 25.0f;
glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far);
Należy tu zwrócić uwagę na parametr pola widzenia
Ponieważ macierz projekcji nie zmienia się w zależności od kierunku, możemy ją ponownie wykorzystać dla każdej z 6 macierzy transformacji. Potrzebujemy innej macierzy widoku na każdy kierunek. Za pomocą
std::vector<glm::mat4> shadowTransforms;
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3( 1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3(-1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 1.0, 0.0), glm::vec3(0.0, 0.0, 1.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3( 0.0,-1.0, 0.0), glm::vec3(0.0, 0.0,-1.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0, 1.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0,-1.0), glm::vec3(0.0,-1.0, 0.0));
Tutaj tworzymy 6 macierzy widoków i mnożymy je za pomocą macierzy projekcji, aby uzyskać w sumie 6 różnych macierzy transformacji przestrzeni światła. Parametr target
Te macierze transformacji są wysyłane do shaderów, które renderują cubemapę głębokości.
Shadery głębi
Aby wyrenderować wartości głębokości do cubemapy głębokości, potrzebujemy w sumie trzech shaderów: Vertex Shadera i Fragment Shadera oraz Geometry Shadera.
Geometry Shader będzie shaderem odpowiedzialnym za przekształcanie wszystkich wierzchołków przestrzeni świata do 6 różnych przestrzeni światła. Dlatego Vertex Shader po prostu przekształca wierzchołki do przestrzeni świata i kieruje je do Geometry Shadera:
#version 330 core
layout (location = 0) in vec3 aPos;
uniform mat4 model;
void main()
{
gl_Position = model * vec4(aPos, 1.0);
}
Następnie Geometry Shader przyjmuje jako dane wejściowe 3 wierzchołki trójkąta i tablicę uniform macierzy transformacji przestrzeni światła. Następnie Geometry Shader przekształca wierzchołki w przestrzenie światła; tutaj robi się interesująco.
Geometry Shader ma wbudowaną zmienną o nazwie gl_Layer, która określa, do której ścianki cubemapy ma zostać wyemitowany prymityw. W sam sobie Geometry Shader przesyła swoje prymitywy w dół potoku renderowania, ale kiedy aktualizujemy tę zmienną, możemy kontrolować, do której ścianki cubemapy wykonujemy renderowanie dla każdego prymitywu. To oczywiście działa tylko wtedy, gdy do aktywnego framebuffera dołączona jest tekstura z cubemapą.
#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices=18) out;
uniform mat4 shadowMatrices[6];
out vec4 FragPos; // FragPos from GS (output per emitvertex)
void main()
{
for(int face = 0; face < 6; ++face)
{
gl_Layer = face; // built-in variable that specifies to which face we render.
for(int i = 0; i < 3; ++i) // for each triangle's vertices
{
FragPos = gl_in[i].gl_Position;
gl_Position = shadowMatrices[face] * FragPos;
EmitVertex();
}
EndPrimitive();
}
}
Ten Geometry Shader powinien być stosunkowo prosty. Jako dane wejściowe przyjmujemy trójkąt i wyprowadzamy w sumie 6 trójkątów (6 * 3 wierzchołki, co równa się 18 wierzchołkom). W funkcji
W ostatnim tutorialu użyliśmy pustego Fragment Shadera i pozwoliliśmy OpenGL określić wartości głębokości mapy głębi. Tym razem będziemy obliczać naszą własną (liniową) głębokość jako odległość liniową między pozycją każdego fragmentu a pozycją źródła światła. Obliczanie własnych wartości głębokości sprawia, że późniejsze obliczenia cieni są nieco bardziej intuicyjne.
#version 330 core
in vec4 FragPos;
uniform vec3 lightPos;
uniform float far_plane;
void main()
{
// get distance between fragment and light source
float lightDistance = length(FragPos.xyz - lightPos);
// map to [0;1] range by dividing by far_plane
lightDistance = lightDistance / far_plane;
// write this as modified depth
gl_FragDepth = lightDistance;
}
Fragment Shader przyjmuje jako dane wejściowe FragPos z Geometry Shadera, wektora położenia światła i wartość dalekiej płaszczyzny frustum. Pobieramy odległość między fragmentem a źródłem światła, mapujemy je do zakresu [0, 1] i zapisujemy jako wartość głębi fragmentu.
Renderowanie sceny za pomocą tych shaderów i aktywnego obiektu framebuffera, do którego podłączona jest cubemapa, powinno dać ci całkowicie wypełnioną mapę głębokości dla obliczeń cieni.
Mapy cieni świateł punktowych
Po ustawieniu wszystkiego nadszedł czas, aby wyrenderować rzeczywiste cienie świateł punktowych. Procedura jest podobna do tej z samouczka o shadow mappingu dla świateł kierunkowych, chociaż tym razem wiążemy teksturę cubemapy zamiast tekstury 2D jako mapy głębi, a także przekazujemy dalszą płaszczyznę macierzy projekcji światła do shaderów.
glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
shader.use();
// ... send uniforms to shader (including light's far_plane value)
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
// ... bind other textures
RenderScene();
Tutaj funkcja
Vertex Shader i Fragment Shader są w dużej mierze podobne do oryginalnych shaderów shadow mappingu: różnice polegają na tym, że Fragment Shader nie wymaga już położenia fragmentu w przestrzeni światła, ponieważ możemy teraz próbkować wartości głębokości za pomocą wektora kierunkowego.
Z tego powodu Vertex Shader nie musi już przekształcać swoich wektorów pozycji do przestrzeni światła, abyśmy mogli wykluczyć zmienną FragPosLightSpace:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
out vec2 TexCoords;
out VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
void main()
{
vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
vs_out.Normal = transpose(inverse(mat3(model))) * aNormal;
vs_out.TexCoords = aTexCoords;
gl_Position = projection * view * model * vec4(aPos, 1.0);
}
Kod cieniowania Blinna-Phonga Fragment Shadera jest dokładnie taki sam jak wcześniej z mnożeniem cieni na końcu:
#version 330 core
out vec4 FragColor;
in VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
} fs_in;
uniform sampler2D diffuseTexture;
uniform samplerCube depthMap;
uniform vec3 lightPos;
uniform vec3 viewPos;
uniform float far_plane;
float ShadowCalculation(vec3 fragPos)
{
[...]
}
void main()
{
vec3 color = texture(diffuseTexture, fs_in.TexCoords).rgb;
vec3 normal = normalize(fs_in.Normal);
vec3 lightColor = vec3(0.3);
// ambient
vec3 ambient = 0.3 * color;
// diffuse
vec3 lightDir = normalize(lightPos - fs_in.FragPos);
float diff = max(dot(lightDir, normal), 0.0);
vec3 diffuse = diff * lightColor;
// specular
vec3 viewDir = normalize(viewPos - fs_in.FragPos);
vec3 reflectDir = reflect(-lightDir, normal);
float spec = 0.0;
vec3 halfwayDir = normalize(lightDir + viewDir);
spec = pow(max(dot(normal, halfwayDir), 0.0), 64.0);
vec3 specular = spec * lightColor;
// calculate shadow
float shadow = ShadowCalculation(fs_in.FragPos);
vec3 lighting = (ambient + (1.0 - shadow) * (diffuse + specular)) * color;
FragColor = vec4(lighting, 1.0);
}
Istnieje kilka subtelnych różnic: kod oświetlenia jest taki sam, ale mamy teraz uniform samplerCube, a funkcja 1.0, gdy fragment jest w cieniu lub 0.0, gdy nie jest. Używamy obliczonego składnika cienia, aby wpłynąć na rozproszone i lustrzane elementy oświetlenia.
W dużym stopniu różni się zawartość funkcji
Pierwszą rzeczą, którą musimy zrobić, to pobrać głębokość z cubemapy. Jak możesz sobie przypomnieć z części tutoriala o cubemapach, to zapisaliśmy głębokość jako liniową odległość między fragmentem a pozycją światła; podejmiemy podobne podejście:
float ShadowCalculation(vec3 fragPos)
{
vec3 fragToLight = fragPos - lightPos;
float closestDepth = texture(depthMap, fragToLight).r;
}
Tutaj bierzemy różnicę między pozycją fragmentu a pozycją światła i wykorzystujemy ten wektor jako wektor kierunkowy do próbkowania cubemapy. Wektor kierunkowy nie musi być wektorem jednostkowym, aby pobierać próbki z cubemapy, więc nie ma potrzeby normalizowania go. Wynikowa wartość closestDepth jest znormalizowaną wartością głębokości między źródłem światła i jego najbliższym widocznym fragmentem.
Wartość closestDepth jest obecnie w zakresie [0, 1], więc najpierw przekształcamy ją z powrotem do zakresu [0, far_plane] przez pomnożenie jej przez far_plane.
closestDepth *= far_plane;
Następnie pobieramy wartość głębokości między bieżącym fragmentem a źródłem światła, które możemy łatwo uzyskać, pobierając długość fragToLight z dzięki obliczeniu wartości głębokości w cubemapie:
float currentDepth = length(fragToLight);
Zwraca to wartość głębokości w tym samym (lub większym) zakresie, co closestDepth.
Teraz możemy porównać obie wartości głębokości, aby zobaczyć, która jest bliżej i określić, czy bieżący fragment jest w cieniu. Uwzględniamy również bias cienia, więc nie dostaniemy artefaktu shadow acne, co omówiono w poprzednim samouczku.
float bias = 0.05;
float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
Pełna funkcja
float ShadowCalculation(vec3 fragPos)
{
// get vector between fragment position and light position
vec3 fragToLight = fragPos - lightPos;
// use the light to fragment vector to sample from the depth map
float closestDepth = texture(depthMap, fragToLight).r;
// it is currently in linear range between [0,1]. Re-transform back to original value
closestDepth *= far_plane;
// now get current linear depth as the length between the fragment and light position
float currentDepth = length(fragToLight);
// now test for shadows
float bias = 0.05;
float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
return shadow;
}
Dzięki tym shaderom możemy uzyskać całkiem dobre cienie i tym razem we wszystkich kierunkach punktowego źródła światła. Scena ze światłem punktowym umieszczonym pośrodku prostej sceny będzie wyglądało mniej więcej tak:
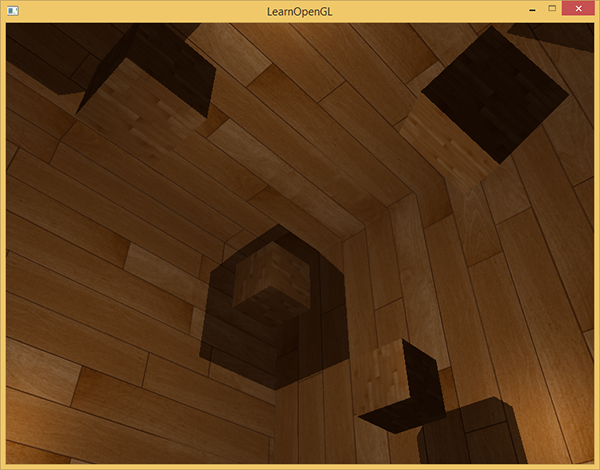
Możesz znaleźć kod źródłowy tego demo tutaj.
Wizualizacja bufora głębi cubemapy
Jeśli jesteś trochę podobny do mnie, prawdopodobnie nie uzyskałeś powyższego efektu za pierwszym razem, więc warto przeprowadzić pewne debugowanie za pomocą jednego sprawdzenia, czy mapa głębi została poprawnie zbudowana. Ponieważ nie mamy już tekstury mapy głębi 2D, wizualizacja mapy głębi staje się nieco mniej oczywista.
Prostą sztuczką do wizualizacji bufora głębi jest wzięcie znormalizowanej wartości (w zakresie [0, 1]) zmiennej closestDepth w funkcji
FragColor = vec4(vec3(closestDepth / far_plane), 1.0);
Rezultatem jest scena w szarościach, w której każdy kolor reprezentuje liniowe wartości głębokości sceny:
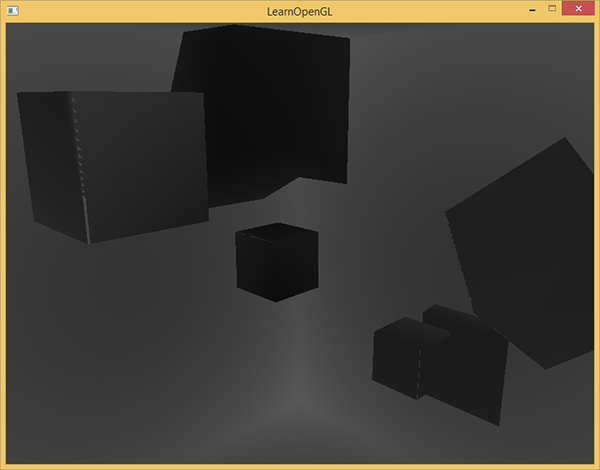
Na zewnętrznej ścianie można również zobaczyć obszary, które mają być zacienione. Jeśli Twoja scena wygląda nieco podobnie, to wiesz, że głębokość cubemapy została poprawnie wygenerowana. W przeciwnym razie prawdopodobnie zrobiłeś coś złego lub użyłeś closestDepth w zakresie [0, far_plane].
PCF
Ponieważ mapy cieni świateł punktowych oparte są na tych samych zasadach co tradycyjny shadow mapping, ma również te same artefakty zależne od rozdzielczości. Jeśli przybliżysz się do cieni, ponownie zobaczysz postrzępione krawędzie.
Jeśli weźmiemy ten sam prosty filtr PCF z poprzedniego samouczka i dodamy trzeci wymiar (ponieważ potrzebujemy wektorów kierunkowych 3D do próbkowania z cubemapy) otrzymamy:
float shadow = 0.0;
float bias = 0.05;
float samples = 4.0;
float offset = 0.1;
for(float x = -offset; x < offset; x += offset / (samples * 0.5))
{
for(float y = -offset; y < offset; y += offset / (samples * 0.5))
{
for(float z = -offset; z < offset; z += offset / (samples * 0.5))
{
float closestDepth = texture(depthMap, fragToLight + vec3(x, y, z)).r;
closestDepth *= far_plane; // Undo mapping [0;1]
if(currentDepth - bias > closestDepth)
shadow += 1.0;
}
}
}
shadow /= (samples * samples * samples);
Kod nie różni się zbytnio od tego, co mieliśmy w tradycyjnym shadow mappingu. Tutaj obliczamy przesunięcia tekstur w sposób dynamiczny na podstawie liczby próbek, które chcielibyśmy zastosować w każdej osi i bierzemy 3 razy więcej samples ilość podpróbek, które następnie uśredniamy na końcu.
Cienie wyglądają teraz o wiele bardziej miękko i gładko i dają o wiele bardziej wiarygodne wyniki.
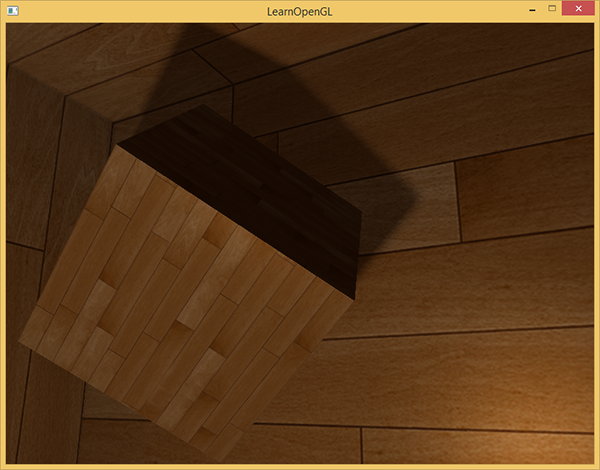
Jednak przy samples ustawionym na 4.0 pobieramy w sumie 64 próbek z każdego fragmentu, co jest dużą ilością!
Ponieważ większość z tych próbek jest zbędna, ponieważ próbkują one blisko oryginalnego wektora kierunku, może być bardziej sensowne, aby próbkować tylko w prostopadłych kierunkach wektora kierunku próbkowania. Ponieważ jednak nie ma (łatwego) sposobu ustalenia, które pod-kierunki są zbędne, staje się to trudne. Jedną z sztuczek, którą możemy zastosować, jest wyznaczenie szeregu kierunków przesunięcia, które można z grubsza oddzielić, np. każdy z nich wskazuje w zupełnie innym kierunku, zmniejszając liczbę pod-kierunków, które są blisko siebie. Poniżej mamy tablicę maksymalnie 20 kierunków przesunięcia:
vec3 sampleOffsetDirections[20] = vec3[]
(
vec3( 1, 1, 1), vec3( 1, -1, 1), vec3(-1, -1, 1), vec3(-1, 1, 1),
vec3( 1, 1, -1), vec3( 1, -1, -1), vec3(-1, -1, -1), vec3(-1, 1, -1),
vec3( 1, 1, 0), vec3( 1, -1, 0), vec3(-1, -1, 0), vec3(-1, 1, 0),
vec3( 1, 0, 1), vec3(-1, 0, 1), vec3( 1, 0, -1), vec3(-1, 0, -1),
vec3( 0, 1, 1), vec3( 0, -1, 1), vec3( 0, -1, -1), vec3( 0, 1, -1)
);
Następnie możemy zmodyfikować algorytm PCF do pobrania ustalonej ilości próbek z sampleOffsetDirections i użyć ich do spróbkowania cubemapy. Zaletą jest to, że potrzebujemy dużo mniej próbek, aby uzyskać wizualnie podobne wyniki do pierwszego algorytmu PCF.
float shadow = 0.0;
float bias = 0.15;
int samples = 20;
float viewDistance = length(viewPos - fragPos);
float diskRadius = 0.05;
for(int i = 0; i < samples; ++i)
{
float closestDepth = texture(depthMap, fragToLight + sampleOffsetDirections[i] * diskRadius).r;
closestDepth *= far_plane; // Undo mapping [0;1]
if(currentDepth - bias > closestDepth)
shadow += 1.0;
}
shadow /= float(samples);
Tutaj dodajemy przesunięcia do określonego diskRadius wokół oryginalnego wektora kierunkowego fragToLight, aby pobrać próbkę z cubemapy.
Inną ciekawą sztuczką, którą możemy tutaj zastosować jest to, że możemy zmienić diskRadius na podstawie odległości od fragmentu; w ten sposób możemy zwiększyć promień przesunięcia o odległość do widza, co powoduje, że cienie stają się bardziej miękkie w oddali i ostrzejsze w pobliżu.
float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0;
Wyniki tego algorytmu PCF dają równie dobre, jeśli nie lepsze, wyniki miękkich cieni:
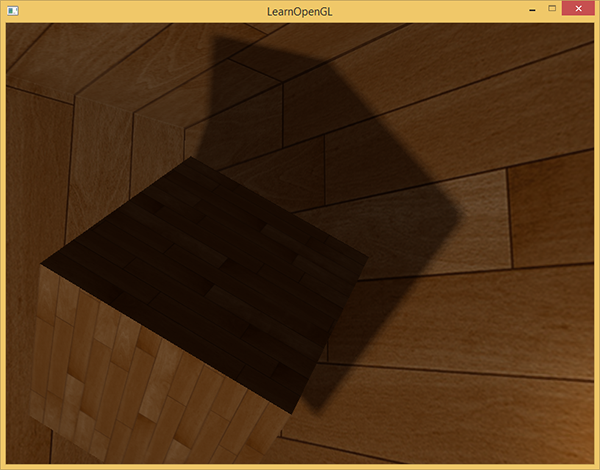
Oczywiście, bias, który dodajemy do każdej próbki, jest wysoce oparty na kontekście i zawsze będzie wymagał ulepszenia w zależności od rodzaju sceny, z którą pracujesz. Pobaw się z wszystkimi wartościami i zobacz, jak wpływają one na scenę.
Finalny kod możesz znaleźć tutaj.
Powinienem wspomnieć, że używanie shaderów geometrii do generowania mapy głębi nie zawsze jest szybsze niż renderowanie sceny 6 razy dla każdej ścianki. Używanie takiego shadera geometrii ma własne kary wydajności, które mogą przewyższać wzrost wydajności korzystania z jednego z nich. Zależy to oczywiście od rodzaju środowiska, konkretnych sterowników karty graficznej itp., Jeśli naprawdę zależy Ci na wydajności, upewnij się, że profilujesz obie metody i wybierasz bardziej wydajną dla swojej sceny. Osobiście wolę używanie Geometry Shaderów do mapowania cieni, ponieważ uważam je za bardziej intuicyjne w użyciu.
Dodatkowe materiały
- Shadow Mapping for point light sources in OpenGL: tutorial o mapach cieni świateł punktowych autorstwa sunandblackcat.
- Multipass Shadow Mapping With Point Lights: tutorial o mapach cieni świateł punktowych autorstwa ogldev.
- Omni-directional Shadows: zestaw slajdów o mapach cieni świateł punktowych autorstwa Petera Houski.