This is the Polish translation of Advanced-Lighting/Normal-Mapping article of learnopengl.com tutorial series.
Wszystkie nasze sceny są wypełnione wielokątami, z których każda składa się z setek, a może tysięcy trójkątów. Poprawiliśmy realizm poprzez wklejenie tekstur 2D na tych trójkątach, aby nadać im dodatkowych szczegółów, ukrywając fakt, że wielokąty składają się z maleńkich płaskich trójkątów. Tekstury pomagają, ale gdy przyjrzeć się im bliżej, nadal łatwo jest dostrzec leżące pod nimi płaskie powierzchnie. Większość prawdziwych powierzchni nie jest jednak płaska i wykazuje dużo (wyboistych) detali.
Na przykład weź ceglaną powierzchnię. Powierzchnia ceglana ma dość szorstką powierzchnię i oczywiście nie jest całkowicie płaska: zawiera zatopione paski cementowe i wiele drobnych dziur i pęknięć. Gdybyśmy oglądali taką ceglaną powierzchnię w oświetlonej scenie, imersja ulegnie łatwemu zerwaniu. Poniżej widać teksturę cegły nałożoną na płaską powierzchnię oświetloną światłem punktowym.
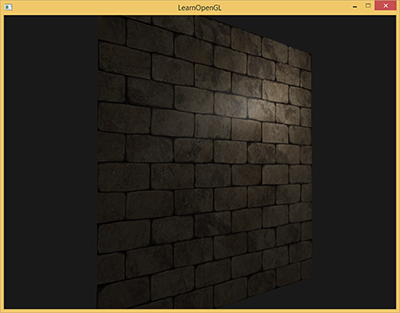
Oświetlenie nie uwzględnia żadnych drobnych pęknięć i dziur i całkowicie ignoruje głębokie paski między cegłami; powierzchnia wygląda idealnie płasko. Możemy częściowo rozwiązać płaskość za pomocą mapy specular, aby udawać, że niektóre powierzchnie są mniej oświetlone ze względu na głębokość lub inne szczegóły, ale to raczej hack niż rzeczywiste rozwiązanie. To, czego potrzebujemy, to sposób informowania systemu oświetleniowego o wszystkich drobnych zagłębianiach w powierzchni.
Jeśli pomyślimy o tym z perspektywy światła: w jaki sposób powierzchnia jest oświetlona jako całkowicie płaska powierzchnia? Odpowiedzią jest wektor normalny powierzchni. Z punktu widzenia algorytmu oświetleniowego jedynym sposobem, w jaki określa on kształt obiektu, jest jego prostopadły wektor normalny. Powierzchnia ceglana ma tylko jeden normalny wektor, w wyniku czego powierzchnia jest równomiernie oświetlona w oparciu o kierunek tego normalnego wektora. Co się stanie, jeśli zamiast wektora normalnego dla powierzchni, która jest taka sama dla każdego fragmentu, użyjemy normalnych dla każdego fragmentu, który jest inny dla każdego fragmentu? W ten sposób możemy nieznacznie odbiegać od normalnego wektora na podstawie drobnych szczegółów powierzchni; w rezultacie daje to złudzenie, że powierzchnia jest o wiele bardziej złożona:

Używając wektorów normalnych per fragment, możemy oszukać oświetlenie, aby uwierzyło, że powierzchnia składa się z maleńkich małych płaszczyzn (prostopadłych do normalnych wektorów), co nadaje powierzchni ogromną szczegółowość. Ta technika posługiwania się normalnymi fragmentów w porównaniu do normalnych powierzchni jest nazywana
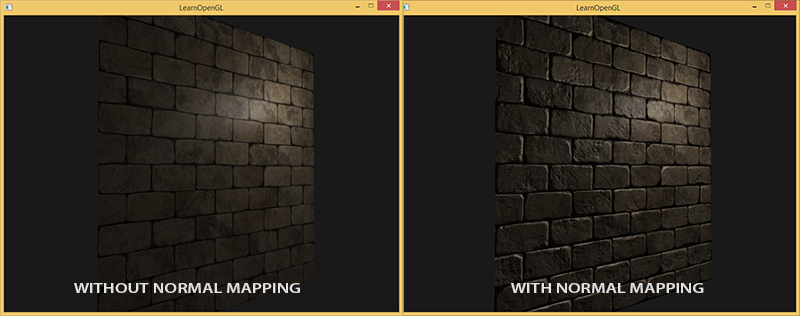
Jak widać, daje to ogromny wzrost szczegółowości i relatywnie niskim kosztem. Ponieważ zmienimy tylko wektory normalne per fragment, nie ma potrzeby zmiany żadnego równania oświetlenia. Przekazujemy teraz wektor normalny dla fragmentu, zamiast interpolowanego wektora normalnego powierzchni do algorytmu oświetlenia. Oświetlenie jest tym, co nadaje powierzchni detal.
Normal mapping
Aby normal mapping działał, potrzebujemy wektora normalnego per-fragment. Podobnie do tego, co zrobiliśmy z mapami diffuse i mapami specular, możemy użyć tekstury 2D do przechowywania danych per-fragment. Oprócz danych kolorów i oświetlenia możemy również przechowywać wektory normalne w teksturach 2D. W ten sposób możemy pobierać próbki z tekstury 2D, aby uzyskać wektor normalny dla tego konkretnego fragmentu.
Podczas gdy wektory normalne są obiektami geometrycznymi, a tekstury są generalnie używane jako zbiory informacji o kolorach, przechowywanie wektorów normalnych w teksturze może nie być oczywiste. Jeśli myślisz o wektorach kolorów w teksturze, są one reprezentowane jako wektory 3D z komponentami r, g i b. Możemy podobnie przechowywać składowe x, y i z wektora normalnego w odpowiednich składnikach kolorów. Wektory normalne mieszczą się w zakresie od -1 do 1, więc najpierw są odwzorowane na zakres [0, 1]:
vec3 rgb_normal = normal * 0.5 + 0.5; // transforms from [-1,1] to [0,1]
W przypadku wektorów normalnych przekształconych w taki składnik koloru RGB można zapisać wektor normalny per-fragment na podstawie kształtu powierzchni do tekstury 2D. Przykład

Ta (i prawie wszystkie mapy normalnych, które znajdziesz w Internecie) będą miały niebieski odcień. Dzieje się tak, ponieważ wszystkie normalne są skierowane na zewnątrz w kierunku dodatniej osi Z, która wynosi $(0, 0, 1)$: i mapuje się na niebieski kolor. Nieznaczne odchylenia w kolorze oznaczają wektory normalne, które są nieco przesunięte względem ogólnego dodatniego kierunku z, dając wrażenie głębi tekstury. Na przykład widać, że na górze każdej cegły kolor ma tendencję do bycia bardziej zielonym, co ma sens, ponieważ górna strona cegły ma wektory normalne wskazujące bardziej w dodatnim kierunku y $(0, 1, 0)$, która mapuje się na kolor zielony!
Za pomocą prostej płaszczyzny, patrzącej na dodatnią oś Z, możemy wziąć tę teksturę diffuse i tą mapę normalnych, aby wyrenderować obraz z poprzedniej sekcji. Zwróć uwagę, że podlinkowana mapa normalnych różni się od tej pokazanej powyżej. Powodem tego jest fakt, że OpenGL odczytuje współrzędne tekstury ze współrzędnymi y (lub V) odwróconymi w stosunku do tego jak te tekstury są generowane. Podlinkowana mapa normalnych ma odwrócony swój komponent y (lub zielony) (widać, że zielone kolory są teraz skierowane w dół); jeśli nie weźmiesz tego pod uwagę, oświetlenie będzie nieprawidłowe. Załaduj obie tekstury, połącz je z odpowiednimi jednostkami tekstur i wyrenderuj płaszczyznę z następującymi zmianami w Fragment Shaderze:
uniform sampler2D normalMap;
void main()
{
// obtain normal from normal map in range [0,1]
normal = texture(normalMap, fs_in.TexCoords).rgb;
// transform normal vector to range [-1,1]
normal = normalize(normal * 2.0 - 1.0);
[...]
// proceed with lighting as normal
}
Tutaj odwracamy proces mapowania normalnych na kolory RGB, zmieniając próbkowany kolor normalny z zakresu [0, 1] z powrotem na zakres [-1, 1], a następnie używamy spróbkowanych wektorów normalnych dla obliczeń oświetlenia. W tym przypadku użyliśmy shadera Blinna-Phonga.
Powoli przesuwając źródło światła w czasie, uzyskujesz poczucie głębi używając mapy normalnych. Uruchomienie tego przykładu normal mappingu daje dokładnie takie same wyniki, jak pokazano na początku tego samouczka:
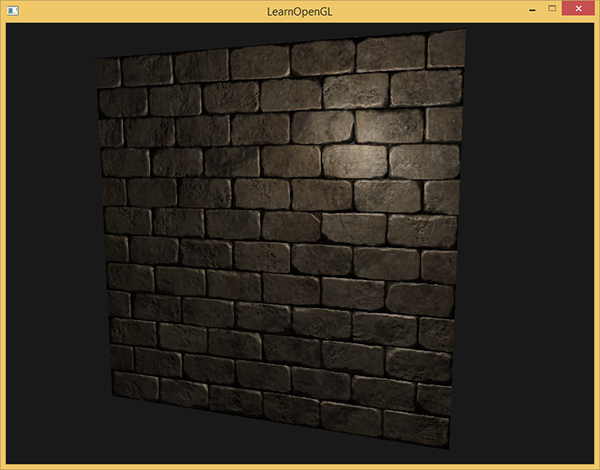
Istnieje jednak jedna kwestia, która znacznie ogranicza korzystanie z map normalnych. Mapa normalnych, której używaliśmy, miała wektory normalne, które z grubsza wskazywały na dodatni kierunek z. To zadziałało, ponieważ wektor normalny płaszczyzny również wskazywał dodatni kierunek z. Co by się jednak stało, gdybyśmy użyli tej samej mapy normalnych na płaszczyźnie leżącej na ziemi z wektorem normalnym wskazującym w kierunku dodatnim osi y?
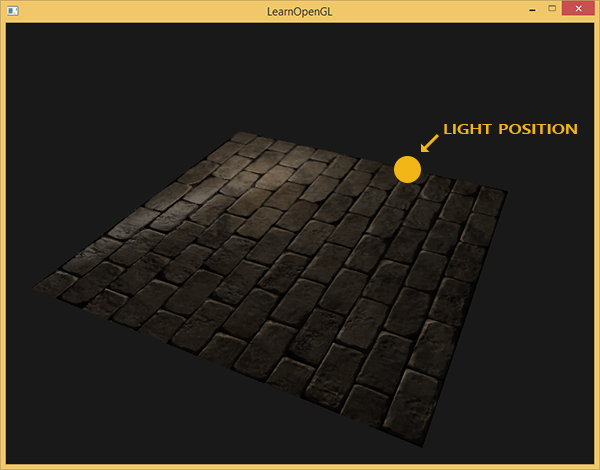
Oświetlenie nie wygląda dobrze! Dzieje się tak, ponieważ próbkowane wartości normalnych tej płaszczyzny nadal wskazują z grubsza w dodatnim kierunku z, nawet jeśli powinny wskazywać na dodatni kierunek y. W rezultacie oświetlenie uważa, że wektory normalne powierzchni są takie same jak wcześniej, gdy powierzchnia wciąż “patrzyła” w kierunku dodatnim z; zatem oświetlenie jest nieprawidłowe. Poniższy obrazek pokazuje, jak wyglądają wektory normalne na tej powierzchni:

Widać, że wszystkie wektory normalne z grubsza wskazują na dodatni kierunek z, podczas gdy powinny wskazywać wzdłuż wektora normalnego powierzchni w dodatnim kierunku y. Możliwym rozwiązaniem tego problemu jest zdefiniowanie mapy normalnej dla każdego możliwego kierunku powierzchni. W przypadku sześcianu potrzebowalibyśmy 6 map normalnych, ale w przypadku zaawansowanych modeli, które mogą mieć więcej niż setki możliwych kierunków powierzchni, staje się to niewykonalne.
Inne, a także nieco trudniejsze rozwiązanie działa poprzez obliczanie oświetlenia w innej przestrzeni współrzędnych: przestrzeń współrzędnych, w której wektory normalne mapy normalnych zawsze wskazują z grubsza w kierunku dodatnim z; wszystkie inne wektory światła są następnie transformowane względem tego dodatniego kierunku z. W ten sposób zawsze możemy korzystać z tej samej mapy normalnych, niezależnie od orientacji. Ta przestrzeń współrzędnych nazywa się
Przestrzeń stycznych
Wektory normalne na mapie normalnych wyrażane są w przestrzeni stycznych, gdzie normalne zawsze wskazują z grubsza dodatni kierunek z. Przestrzeń stycznych to przestrzeń, która jest lokalna na powierzchni trójkąta: wartości normalnych odnoszą się do lokalnej ramki odniesienia poszczególnych trójkątów. Pomyśl o tym, jako o lokalnej przestrzeni wektorów mapy normalnych; wszystkie są zdefiniowane, wskazując w dodatnim kierunku z niezależnie od ostatecznego kierunku. Za pomocą określonej macierzy możemy następnie przekształcić wektory normalne z tej przestrzeni lokalnej stycznych do przestrzeni świata lub widoku, ustawiając je wzdłuż końcowego kierunku mapowanej powierzchni.
Powiedzmy, że mamy nieprawidłową powierzchnię z normal mappingiem z poprzedniej sekcji patrzącą w dodatnim kierunku y. Mapa normalnych jest definiowana w przestrzeni stycznych, więc jednym ze sposobów rozwiązania problemu jest obliczenie macierzy w celu przekształcenia normalnych z przestrzeni stycznych na inną przestrzeń, tak aby były wyrównane z wektorem normalnym powierzchni: wektory normalne będą wtedy wskazywać z grubsza w dodatnim kierunku y. Wielką zaletą przestrzeni stycznych jest to, że możemy obliczyć taką macierz dla dowolnego typu powierzchni, abyśmy mogli odpowiednio ustawić kierunek z przestrzeni stycznych do wektora normalnego powierzchni.
Taka macierz nazywa się macierzą
Znamy już wektor skierowany w górę, który jest wektorem normalnym powierzchni. Wektor skierowany w prawo i w przód to odpowiednio wektor tangent i bitangent. Poniższy obraz powierzchni pokazuje wszystkie trzy wektory na powierzchni:
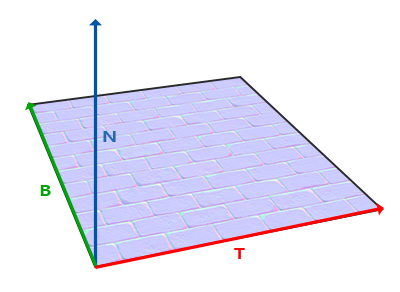
Obliczanie wektora tangent i bitangent nie jest tak proste, jak obliczanie wektora normalnego. Na podstawie obrazu widzimy, że kierunek wektora tangent i bitangent mapy normalnych jest zgodny z kierunkiem, w którym definiujemy współrzędne tekstury powierzchni. Wykorzystamy ten fakt do obliczenia wektorów tangent i bitangent dla każdej powierzchni. Obliczenie ich wymaga trochę matematyki; spójrz na następujący obraz:
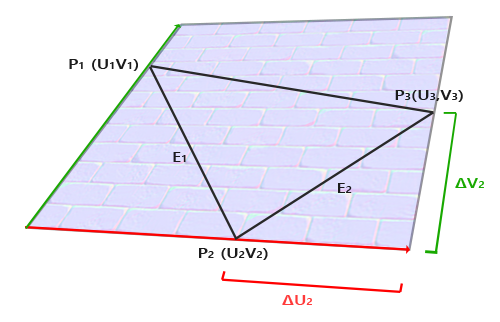
Z obrazu widzimy, że różnice współrzędnych tekstury krawędzi $E_2$ trójkąta oznaczają, że $\Delta U_2$ i $\Delta V_2$ są wyrażone w tym samym kierunku co wektor tangent $T$ i wektor bitangent $B$. Z tego powodu możemy zapisać krawędzie $E_1$ i $E_2$ trójkąta jako liniową kombinację wektora tangent $T$ i wektora bitangent $B$:
\[E_1 = \Delta U_1T + \Delta V_1B\] \[E_2 = \Delta U_2T + \Delta V_2B\]Co możemy również napisać jako:
\[(E_{1x}, E_{1y}, E_{1z}) = \Delta U_1(T_x, T_y, T_z) + \Delta V_1(B_x, B_y, B_z)\] \[(E_{2x}, E_{2y}, E_{2z}) = \Delta U_2(T_x, T_y, T_z) + \Delta V_2(B_x, B_y, B_z)\]Możemy obliczyć $E$ jako wektor różnicy między dwiema pozycjami wektoraów oraz $\Delta U$ i $\Delta V$ jako różnicę współrzędnych tekstury. Zostały nam wówczas dwie niewiadome (tangent $T$ i bitangent $B$) i dwa równania. Być może pamiętasz ze swoich lekcji algebry, że to pozwala nam rozwiązać $T$ i $B$.
Ostatnie równania pozwalają na zapisanie tego w innej formie - mnożenia macierzy:
\[\begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix} \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}\]Spróbuj zwizualizować mnożenie macierzowe w swojej głowie i sprawdź, czy jest to rzeczywiście to samo równanie. Zaletą przepisywania równań w postaci macierzowej jest to, że rozwiązanie dla $T$ i $B$ staje się bardziej oczywiste. Jeśli pomnożymy obie strony równania przez odwrotność macierzy $\Delta U \Delta V$, otrzymamy:
\[\begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix}^{-1} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}\]To pozwala nam rozwiązać $T$ i $B$. Wymaga to od nas obliczenia odwrotności macierzy współrzędnych tekstury delta. Nie wchodzę w szczegóły matematyczne obliczania odwrotności macierzy, ale z grubsza przekłada się to na 1 przez wyznacznik macierzy pomnożonej przez jej macierz dołączoną:
\[\begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} = \frac{1}{\Delta U_1 \Delta V_2 - \Delta U_2 \Delta V_1} \begin{bmatrix} \Delta V_2 & -\Delta V_1 \\ -\Delta U_2 & \Delta U_1 \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix}\]To końcowe równanie daje nam wzór do obliczenia wektora $T$ i wektora $B$ z dwóch krawędzi trójkąta i jego współrzędnych tekstury.
Nie martw się, jeśli tak naprawdę nie rozumiesz matematyki stojącej za tym. Dopóki rozumiesz, że możemy obliczyć wektory tangent i bitangent z wierzchołków trójkąta i jego współrzędnych tekstury (ponieważ współrzędne tekstury są w tej samej przestrzeni co wektory styczne) to jesteś na dobrej drodze.
Ręczne obliczanie wektorów tangent i bitangent
W scenie demo mieliśmy prostą płaszczyznę 2D patrzącą w kierunku pozytywnej osi z. Tym razem chcielibyśmy zaimplementować normal mapping przy użyciu przestrzeni stycznych, abyśmy mogli ustawić tę płaszczyznę jak chcemy i aby normal mapping nadal działał. Korzystając z omawianej wcześniej matematyki, będziemy ręcznie obliczać wektory tangent i bitangent tej powierzchni.
Zakładając, że płaszczyzna jest zbudowana z następujących wektorów (z 1, 2, 3 i 1, 3, 4 jako dwoma trójkątami):
// pozycje
glm::vec3 pos1(-1.0, 1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3( 1.0, -1.0, 0.0);
glm::vec3 pos4( 1.0, 1.0, 0.0);
// współrzędne tekstury
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// wektor normalny
glm::vec3 nm(0.0, 0.0, 1.0);
Najpierw obliczamy krawędzie pierwszego trójkąta i współrzędne delty UV:
glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;
Dzięki wymaganym danym do obliczenia wektorów tangent i bitangent możemy zacząć stosować równanie z poprzedniej sekcji:
float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent1 = glm::normalize(tangent1);
bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent1 = glm::normalize(bitangent1);
[...] // podobna procedura do obliczania wektora tangent/bitangent dla drugiego trójkąta płaszczyzny
Najpierw wstępnie obliczamy część ułamkową równania jako f, a następnie dla każdego składnika wektora wykonujemy odpowiednie mnożenie macierzy przez f. Jeśli porównasz ten kod z ostatecznym równaniem, zobaczysz, że jest to bezpośrednie tłumaczenie równania na kod. Na końcu robimy także normalizację, aby upewnić się, że wektory tangent/bitangent są wektorami jednostkowymi.
Ponieważ trójkąt jest zawsze płaski, wystarczy obliczyć pojedynczą parę wektorów tangent/bitangent na trójkąt, ponieważ będą one takie same dla każdego z wierzchołków trójkąta. Należy zauważyć, że większość implementacji (na przykład biblioteki ładujące modele i generatory terenu) generalnie ma trójkąty, które współdzielą wierzchołki z innymi trójkątami. W takim przypadku programiści zwykle wyliczają właściwości wierzchołków, takie jak wektory normalne i tangent/bitangent dla każdego wierzchołka, aby uzyskać bardziej gładki wynik. Trójkąty naszej płaszczyzny również współdzielą niektóre wierzchołki, ale ponieważ oba trójkąty są równoległe do siebie, nie ma potrzeby uśredniania wyników, ale dobrze jest mieć to na uwadze, gdy tylko spotkasz się z taką sytuacją.
Wynikowy wektor tangent i bitangent powinny mieć wartości (1,0,0) i (0,1,0) gdzie razem z wartością wektora normalnego (0,0,1) tworzą ortogonalną macierz TBN. Zwizualizowane na płaszczyźnie wektory TBN wyglądałyby tak:
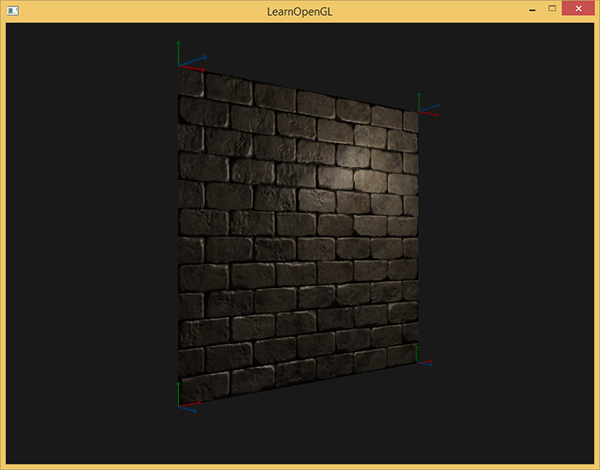
W przypadku wektorów tangent i bitangent dla każdego wierzchołka możemy rozpocząć implementację właściwego algorytmu normal mappingu.
Normal mapping w przestrzeni stycznych
Aby normal mapping działał, najpierw musimy utworzyć macierz TBN w shaderach. W tym celu przekazujemy wcześniej obliczone wektory tangent i bitangent do Vertex Shadera jako atrybuty wierzchołków:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;
Następnie w funkcji
void main()
{
[...]
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
mat3 TBN = mat3(T, B, N)
}
Najpierw transformujemy wszystkie wektory TBN do układu współrzędnych, w którym chcielibyśmy pracować, co w tym przypadku jest przestrzenią świata, jako że mnożymy je tylko z macierzą model. Następnie tworzymy rzeczywistą macierz TBN, bezpośrednio dostarczając konstruktorowi
Technicznie nie ma potrzeby definiowania zmiennej bitangent w Vertex Shader. Wszystkie trzy wektory TBN są prostopadłe do siebie, więc możemy obliczyć sami wektor bitangent w Vertex Shader, po prostu używając iloczynu wektorowego wektorów T i N: vec3 B = cross(N, T);
Skoro mamy macierz TBN, w jaki sposób zamierzamy z niej korzystać? Zasadniczo istnieją dwa sposoby wykorzystania macierzy TBN do normal mappingu. Pokażemy obie z nich:
- Bierzemy macierz TBN, która przekształca dowolny wektor z przestrzeni stycznych do przestrzeni świata, przekazujemy go do Fragment Shadera i przekształcamy próbkowany wektor normalny z przestrzeni stycznych do przestrzeni świata za pomocą macierzy TBN; wektor normalny jest wtedy w tej samej przestrzeni co inne zmienne oświetlenia.
- Bierzemy odwrotność macierzy TBN, która przekształca dowolny wektor z przestrzeni świata do przestrzeni stycznych i używamy tej macierzy, by przekształcić inne odpowiednie zmienne oświetlenia do przestrzeni stycznych poza wektorami normalnymi; wektory normalne są znowu w tej samej przestrzeni co inne zmienne oświetlenia.
Przyjrzyjmy się pierwszemu przypadkowi. Wektor normalny, który pobieramy z mapy normalnych, wyrażany jest w przestrzeni stycznych, podczas gdy inne wektory oświetlenia (pozycja światła i kamery) są wyrażone w przestrzeni świata. Przekazując macierz TBN do Fragment Shadera, możemy pomnożyć próbkowany wektor normalny w przestrzeni stycznych z macierzą TBN, aby przekształcić go do tej samej przestrzeni, co inne zmienne oświetlenia. W ten sposób wszystkie obliczenia oświetlenia (w szczególności iloczyn skalarny) mają sens.
Przesłanie macierzy TBN do Fragment Shadera jest łatwe:
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} vs_out;
void main()
{
[...]
vs_out.TBN = mat3(T, B, N);
}
W Fragment Shader przyjmujemy mat3 jako zmienną wejściową:
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} fs_in;
Dzięki macierzy TBN możemy teraz zaktualizować kod normal mappingu, aby uwzględnić transformację z przestrzeni stycznych do przestrzeni świata:
normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);
normal = normalize(fs_in.TBN * normal);
Ponieważ wynikowy wektor normal znajduje się teraz w przestrzeni świata, nie ma potrzeby zmiany żadnego z pozostałych parametrów kodu cieniowania, ponieważ kod oświetlenia zakłada, że wektor normalny znajduje się w przestrzeni świata.
Przyjrzyjmy się także drugiemu przypadkowi, w którym przyjmujemy odwrotność macierzy TBN, aby przekształcić wszystkie istotne zmienne w przestrzeni świata do przestrzeni, w której znajdują się próbkowane wektory normalne: przestrzeni stycznych. Konstrukcja macierzy TBN pozostaje taka sama, ale najpierw odwróciliśmy macierz przed przesłaniem jej do Fragment Shadera:
vs_out.TBN = transpose(mat3(T, B, N));
Zauważ, że używamy tutaj funkcji
W obrębie Fragment Shadera nie transformujemy wektora normalnego, lecz przekształcamy inne odpowiednie wektory do przestrzeni stycznych, czyli wektory lightDir i viewDir. W ten sposób każdy wektor znów znajduje się w tym samym układzie współrzędnych: w przestrzeni stycznych.
void main()
{
vec3 normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);
vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos);
vec3 viewDir = fs_in.TBN * normalize(viewPos - fs_in.FragPos);
[...]
}
Drugie podejście wydaje się bardziej pracochłonne, a także wymaga większej liczby mnożeń macierzowych w Fragment Shader (które są nieco drogie), więc dlaczego mielibyśmy się przejmować drugim podejściem?
Przekształcanie wektorów z przestrzeni świata do przestrzeni stycznych ma dodatkową zaletę, ponieważ możemy przekształcić wszystkie odpowiednie wektory do przestrzeni stycznych w Vertex Shaderze zamiast w Fragment Shaderze. Działa to, ponieważ lightPos i viewPos nie zmieniają przebiegu każdego Fragment Shadera, a dla fs_in.FragPos możemy również obliczyć jego pozycję w przestrzeni stycznych w Vertex Shader i interpolacja fragmentów wykona swoją pracę. Zasadniczo, nie ma potrzeby przekształcania żadnego wektora do przestrzeni stycznych w Fragment Shaderze, podczas gdy jest to konieczne w pierwszym podejściu, ponieważ próbkowane wektory normalne są specyficzne dla każdego przebiegu Fragment Shadera.
Dlatego zamiast wysyłać odwrotność macierzy TBN do Fragment Shadera, wysyłamy pozycję światła, pozycję kamery i pozycję wierzchołka w przestrzeni stycznych do Fragment Shadera. Oszczędza to nam mnożenia macierzy w Fragment Shader. Jest to dobra optymalizacja, ponieważ Vertex Shader jest wywoływany znacznie rzadziej niż Fragment Shader. Jest to również powód, dla którego podejście to jest często preferowanym podejściem.
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
uniform vec3 lightPos;
uniform vec3 viewPos;
[...]
void main()
{
[...]
mat3 TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vec3(model * vec4(aPos, 0.0));
}
W Fragment Shader używamy tych nowych zmiennych wejściowych do obliczania oświetlenia w przestrzeni stycznych. Ponieważ wektor normalny jest już w przestrzeni stycznych, kod oświetlenia ma sens.
Przy zastosowaniu normal mappingu w przestrzeni stycznych powinniśmy uzyskać podobne wyniki do tego, co mieliśmy na początku tego samouczka, ale tym razem możemy ustawić naszą płaszczyznę w dowolny sposób, a oświetlenie będzie nadal poprawne:
glm::mat4 model;
model = glm::rotate(model, (float)glfwGetTime() * -10.0f, glm::normalize(glm::vec3(1.0, 0.0, 1.0)));
shader.setMat4("model", model);
RenderQuad();
Co rzeczywiście wygląda jak poprawny efekt normal mappingu:
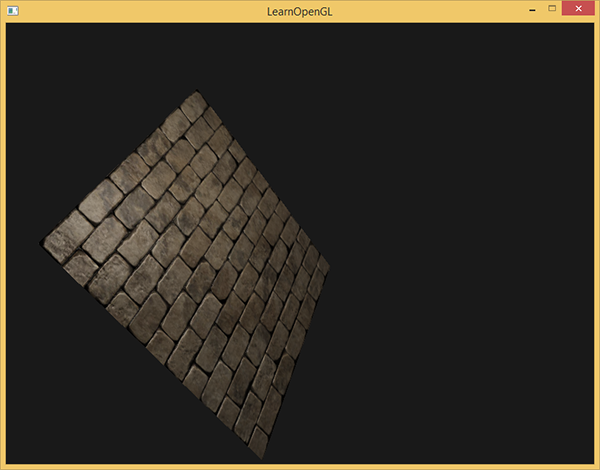
Możesz znaleźć kod źródłowy tutaj.
Złożone obiekty
Pokazaliśmy, w jaki sposób możemy użyć normal mappingu wraz z transformacjami przestrzeni stycznych, ręcznie obliczając wektory tangent i bitangent. Na szczęście dla nas ręczne obliczanie wektorów tangent i bitangent nie jest czymś, co robisz często; w większości przypadków implementujesz to raz w programie ładującym model lub w naszym przypadku używamy naszego modułu ładującego modele przy użyciu biblioteki Assimp.
Assimp ma bardzo użyteczną flagę konfiguracji, którą możemy ustawić podczas ładowania modelu o nazwie aiProcess_CalcTangentSpace. Kiedy flaga aiProcess_CalcTangentSpace zostanie dostarczona do funkcji
const aiScene *scene = importer.ReadFile(
path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace
);
Za pomocą Assimp możemy następnie pobrać obliczone wektory styczne poprzez:
vector.x = mesh->mTangents[i].x;
vector.y = mesh->mTangents[i].y;
vector.z = mesh->mTangents[i].z;
vertex.Tangent = vector;
Następnie musisz również zaktualizować moduł ładujący modele, aby załadować mapy normalnych dla oteksturowanego modelu. Format obiektu wavefront (.obj) eksportuje mapy normalnych nieco inaczej, ponieważ aiTextureType_NORMAL biblioteki Assimp nie ładuje map normalnych, podczas gdy aiTextureType_HEIGHT naprawia ten problem dlatego często ładuję je jako:
vector<Texture> normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal");
Oczywiście jest to inne dla każdego typu załadowanego modelu i formatu pliku. Należy również pamiętać, że aiProcess_CalcTangentSpace nie zawsze działa. Obliczanie stycznych opiera się na współrzędnych tekstury, a niektórzy twórcy modeli wykonują pewne triki ze współrzędnymi tekstur, takie jak np. odbicie lustrzane powierzchni tekstury na modelu, również odzwierciedlając połowę współrzędnych tekstury; daje to niepoprawne wyniki, gdyż dublowanie nie jest brane pod uwagę (Assimp tego nie uwzględnia); model nanokombinezonu na przykład nie wytwarza właściwych stycznych, ponieważ ma odzwierciedlone współrzędne tekstury.
Uruchomienie aplikacji na modelu, który ma odpowiednią teksturę specular i mapę normalnych przy użyciu zaktualizowanego modułu ładującego model, daje wynik nieco podobny do tego:

Jak widać normal mapping zwiększa szczegółowość obiektu.
Używanie map normalnych to także świetny sposób na zwiększenie wydajności twojej sceny. Przed normal mappingiem trzeba było użyć dużej liczby wierzchołków, aby przedstawić dużą liczbę szczegółów na siatce, ale przy normal mappingu możemy przedstawić ten sam poziom szczegółów na siatce przy użyciu znacznie mniejszej liczby wierzchołków. Obraz poniżej autorstwa Paolo Cignoni pokazuje dobre porównanie obu metod:
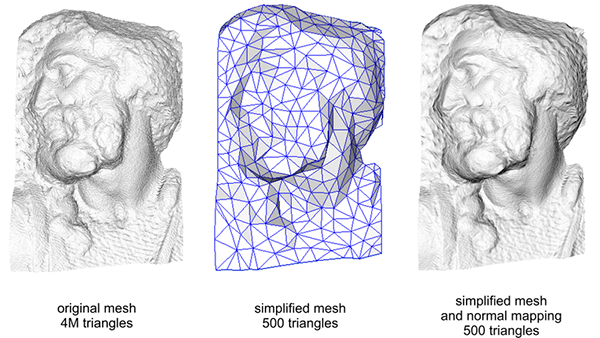
Szczegóły zarówno na siatce o wysokiej liczbie wierzchołków, jak i siatce o niskiej liczbie wierzchołków z normal mappingiem są prawie nie do odróżnienia. Więc normal mapping nie tylko wygląda ładnie, ale jest również świetnym narzędziem do zastąpienia modeli o dużej liczbie wierzchołku, modelami o małej liczbie wierzchołków bez utraty szczegółów.
Ostatnia rzecz
Jest jedna sztuczka, którą chciałbym omówić w odniesieniu do normal mappingu, która nieznacznie poprawia jej jakość bez dodatkowych kosztów.
Gdy wektory styczne są obliczane na większych siatkach, które współdzielą znaczną liczbę wierzchołków, wektory styczne są zwykle uśredniane, aby uzyskać ładne i gładkie wyniki, gdy do tych powierzchni zostanie zastosowany normal mapping. Problem z tym podejściem polega na tym, że trzy wektory TBN mogą skończyć jako nie-prostopadle do siebie, co oznacza, że uzyskana macierz TBN nie będzie już ortogonalna. Normal mapping będzie wyglądał niedokładnie z nieortogonalną macierzą TBN, ale wciąż możemy to poprawić.
Używając matematycznej sztuczki zwanej
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
// re-orthogonalize T with respect to N
T = normalize(T - dot(T, N) * N);
// then retrieve perpendicular vector B with the cross product of T and N
vec3 B = cross(N, T);
mat3 TBN = mat3(T, B, N)
To, choć trochę, poprawia wyniki normal mappingu z niewielkimi dodatkowymi kosztami. Spójrz na koniec filmu Normal Mapping Mathematics, który jest wymieniony w ostatniej sekcji tego samouczka, aby uzyskać doskonałe wyjaśnienie, jak ten proces faktycznie działa.
Dodatkowe materiały
- Tutorial 26: Normal Mapping: tutorial normal mappingu autorstwa ogldev.
- How Normal Mapping Works: film instruktażowy o tym, jak działa normal mapping autorstwa TheBennyBox.
- Normal Mapping Mathematics: podobne wideo autorstwa TheBennyBox o matematyce stojącej za normal mappingiem.
- Tutorial 13: Normal Mapping: tutorial normal mappingu autorstwa opengl-tutorial.org.