This is the Polish translation of Advanced-Lighting/Parallax-Mapping article of learnopengl.com tutorial series.
Mapowanie paralaksy to technika podobna do normal mappingu, ale oparta na innych zasadach. Podobnie jak w przypadku zwykłego normal mappingu, jest to technika, która znacznie zwiększa szczegółowość oteksturowanej powierzchni i daje poczucie głębi. Choć jest to iluzja, mapowanie paralaksy jest o wiele lepsze w uwypuklaniu głębi i wraz z normal mappingiem daje niewiarygodnie realistyczne rezultaty. Chociaż mapowanie paralaksy niekoniecznie jest techniką bezpośrednio związaną z (zaawansowanym) oświetleniem, przedyskutuję ją tutaj, ponieważ ta technika jest logiczną kontynuacją normal mappingu. Zwróć uwagę, że uzyskanie wiedzy na temat normal mappingu, w szczególności o przestrzeni stycznych, jest zdecydowanie zalecane przed opanowaniem mapowania paralaksy.
Mapowanie paralaksy należy do rodziny technik

Po rozłożeniu jej na płaszczyźnie każdy wierzchołek jest przemieszczany w oparciu o próbkowaną wartość wysokości mapy wysokości, przekształcając płaską płaszczyznę na szorstką, nierówną powierzchnię w oparciu o geometryczne właściwości materiału. Na przykład, przyjęcie płaskiej płaszczyzny przemieszczonej za pomocą powyższej mapy wysokości skutkuje następującym obrazem:
Problem z przesuwaniem wierzchołków polega na tym, że płaszczyzna musi składać się z dużej ilości wierzchołków, aby uzyskać realistyczne przesunięcia, w przeciwnym razie przesunięcie będzie zbyt duże. Ponieważ każda powierzchnia płaska może wymagać ponad 1000 wierzchołków, szybko staje się to bardzo kosztowne obliczeniowo. Co by było, gdybyśmy mogli osiągnąć podobny realizm bez potrzeby wstawiania dodatkowych wierzchołków? Co jeśli powiem ci, że powyższa zniekształcona powierzchnia jest faktycznie renderowana tylko z 6 wierzchołkami (lub 2 trójkątami)? Ta pokazana powierzchnia z cegły jest renderowana za pomocą
Ideą mapowania paralaksy jest zmiana współrzędnych tekstury w taki sposób, aby wyglądało tak, jakby powierzchnia fragmentu była wyżej lub niżej niż jest w rzeczywistości, wszystko oparte na kierunku patrzenia i mapie wysokości. Aby zrozumieć, jak to działa, spójrz na następujący obraz naszej ceglanej powierzchni:
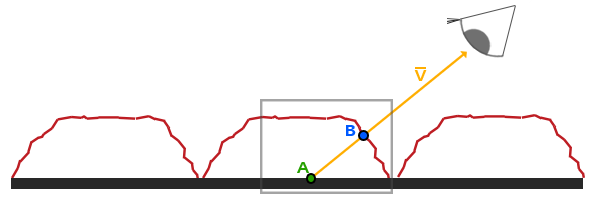
Tutaj chropowata czerwona linia reprezentuje wartości w mapie wysokości jako geometryczną reprezentację powierzchni cegły, a wektor $\color{orange}{\bar{V}}$ reprezentuje wektor kierunku patrzenia skierowany od płaszczyzny do kamery (viewDir). Jeśli płaszczyzna miałaby rzeczywiste przemieszczenie, widz zobaczyłby powierzchnię w punkcie $\color{blue}B$. Ponieważ jednak nasza płaszczyzna nie ma rzeczywistego przesunięcia, kierunek patrzenia uderza w płaską płaszczyznę w punkcie $\color{green}A$, jak się spodziewaliśmy. Mapowanie paralaksy ma na celu skompensowanie współrzędnych tekstury w pozycji fragmentu $\color{green}A$ w taki sposób, aby uzyskać współrzędne tekstury w punkcie $\color{blue}B$. Następnie używamy współrzędnych tekstury w punkcie $\color{blue}B$ dla wszystkich kolejnych próbek tekstury, dzięki czemu wygląda na to, że widz rzeczywiście patrzy na punkt $\color{blue}B$.
Sztuką jest dowiedzieć się, jak uzyskać współrzędne tekstury w punkcie $\color{blue}B$ od punktu $\color{green}A$. Mapowanie paralaksy próbuje rozwiązać ten problem przez skalowanie wektora kierunku $\color{orange}{\bar{V}}$ przez wysokość fragmentu $\color{green}A$. Skalujemy więc długość $\color{orange}{\bar{V}}$, aby była równa wartości próbkowanej z mapy wysokości $\color{green}{H(A)}$ w pozycji fragmentu $\color{green}A$ . Poniższy obrazek pokazuje ten skalowany wektor $\color{brown}{\bar{P}}$:
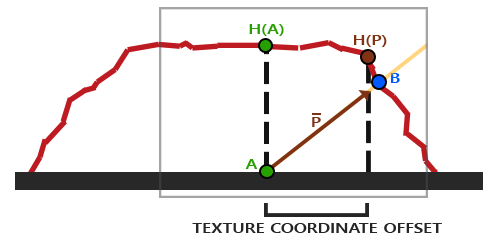
Następnie bierzemy wektor $\color{brown}{\bar{P}}$ i przyjmujemy jego współrzędne, które wyrównują się do płaszczyzny jako przesunięcie współrzędnych tekstury. Działa to dlatego, że wektor $\color{brown}{\bar{P}}$ jest obliczany na podstawie wartości wysokości z mapy wysokości, więc im wyższa jest wysokość fragmentu, tym bardziej zostaje przemieszczona.
Ta mała sztuczka daje dobre wyniki, ale jest jednak bardzo dużym przybliżeniem uzyskania punktu $\color{blue}B$. Kiedy wysokość zmienia się szybko, wyniki wydają się nierealistyczne, ponieważ wektor $\color{brown}{\bar{P}}$ nie będzie blisko punktu $\color{blue}B$, jak widać poniżej:
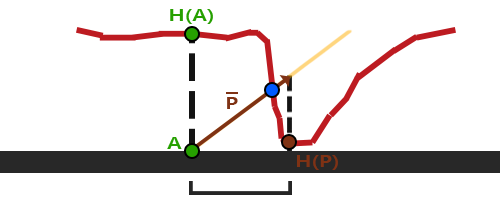
Kolejną kwestią związaną z mapowaniem paralaksy jest to, że trudno jest ustalić, które współrzędne mają zostać pobrane z $\color{brown}{\bar{P}}$, gdy powierzchnia jest dowolnie obracana. Wolimy raczej robić mapowanie paralaksy w innej przestrzeni współrzędnych, w której komponenty x i y wektora $\color{brown}{\bar{P}}$ zawsze wyrównują się z powierzchnią tekstury. Jeśli śledziłeś samouczek normal mapping, prawdopodobnie zgadłeś, jak możemy to zrobić. Chcielibyśmy robić mapowanie paralaksy w przestrzeni stycznych.
Przekształcając wektor kierunkowy fragmentu $\color{orange}{\bar{V}}$ do przestrzeni stycznych, transformowany wektor $\color{brown}{\bar{P}}$ będzie miał wartości x i y wyrównane do wektorów tangent i bitangent powierzchni. Ponieważ wektory tangent i bitangent wskazują w tym samym kierunku co współrzędne tekstury powierzchni, możemy przyjąć komponenty x i y wektora $\color{brown}{\bar{P}}$ jako przesunięcie współrzędnych tekstury, niezależnie od kierunku powierzchni.
Ale wystarczająco dużo o teorii. Zacznijmy wdrażać faktyczne mapowanie paralaksy.
Parallax mapping
Do mapowania paralaksy użyjemy prostej płaszczyzny 2D, dla której obliczamy jej wektor tangent i bitangent przed wysłaniem do GPU; podobnie do tego, co zrobiliśmy w samouczku o normal mappingu. Do płaszczyzny mamy zamiar dołączyć teksturę diffuse, mapę normalnych i displacement map (ang. mapa przesunięcia), które można pobrać, klikając odpowiednie linki. W tym przykładzie użyjemy mapowania paralaksy w połączeniu z normal mappingiem. Ponieważ mapowanie paralaksy daje złudzenie, że zniekształca powierzchnię, to iluzja przestaje działać, gdy oświetlenie jest nieodpowiednie. Ponieważ mapy normalnych są często generowane z map wysokości, użycie mapy normalnych wraz z mapą wysokości zapewnia, że oświetlenie jest dostosowane do przesunięcia.
Być może już zauważyłeś, że mapa przesunięcia, do której link znajduje się powyżej, jest odwrotnością mapy wysokości pokazanej na początku tego samouczka. W przypadku mapowania paralaksy bardziej sensowne jest użycie odwrotności mapy wysokości (znanej również jako
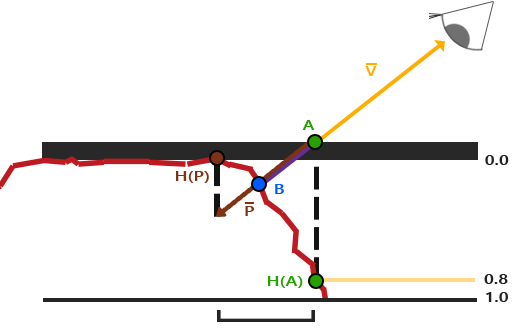
Ponownie mamy punkty $\color{green}A$ i $\color{blue}B$, ale tym razem otrzymujemy wektor $\color{brown}{\bar{P}}$ przez odejmowanie wektora $\color{orange}{\bar{V}}$ od współrzędnych tekstury w punkcie $\color{green}A$. Możemy uzyskać wartości głębokości zamiast wartości wysokości odejmując wartości próbkowanych wysokości od 1.0 w shaderach lub po prostu odwracając wartości tekstur w oprogramowaniu do edycji obrazów, tak jak to zrobiliśmy z mapą głębi w linku powyżej.
Mapowanie paralaksy jest implementowane w Fragment Shader, ponieważ efekt przesunięcia różni się na całej powierzchni trójkąta. W Fragment Shader będziemy musieli obliczyć wektor kierunkowy patrzenia $\color{orange}{\bar{V}}$, więc potrzebujemy pozycji kamery i położenia fragmentu w przestrzeni stycznych. W samouczku normal mappingu mieliśmy Vertex Shader, który przesyłał te wektory w przestrzeni stycznych, więc możemy pobrać dokładną kopię tego Vertex Shadera:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
uniform vec3 lightPos;
uniform vec3 viewPos;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
vs_out.TexCoords = aTexCoords;
vec3 T = normalize(mat3(model) * aTangent);
vec3 B = normalize(mat3(model) * aBitangent);
vec3 N = normalize(mat3(model) * aNormal);
mat3 TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vs_out.FragPos;
}
Należy zauważyć, że w przypadku mapowania paralaksy musimy przesłać aPos i pozycję kamery viewPos w przestrzeni stycznych do Fragment Shadera.
W obrębie Fragment Shadera implementujemy logikę mapowania paralaksy. Cieniowanie fragmentów wygląda tak:
#version 330 core
out vec4 FragColor;
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} fs_in;
uniform sampler2D diffuseMap;
uniform sampler2D normalMap;
uniform sampler2D depthMap;
uniform float height_scale;
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir);
void main()
{
// offset texture coordinates with Parallax Mapping
vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos);
vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir);
// then sample textures with new texture coords
vec3 diffuse = texture(diffuseMap, texCoords);
vec3 normal = texture(normalMap, texCoords);
normal = normalize(normal * 2.0 - 1.0);
// proceed with lighting code
[...]
}
Zdefiniowaliśmy funkcję o nazwie
Zajrzyjmy do funkcji
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{
float height = texture(depthMap, texCoords).r;
vec2 p = viewDir.xy / viewDir.z * (height * height_scale);
return texCoords - p;
}
Ta względnie prosta funkcja jest bezpośrednim tłumaczeniem tego, o czym mówiliśmy do tej pory. Przyjmujemy oryginalne współrzędne tekstury texCoords i używamy ich do spróbkowania wysokości (lub głębokości) z depthMap bieżącego fragmentu $\color{green}{H(A)}$. Następnie obliczamy $\color{brown}{\bar{P}}$ jako komponent x i y w przestrzeni stycznych viewDir podzielonej przez jej składnik z i skalujemy go przez wysokość fragmentu. Wprowadziliśmy także uniform height_scale, aby uzyskać dodatkową kontrolę, ponieważ efekt paralaksy jest zwykle zbyt silny bez dodatkowego parametru skali. Następnie odejmujemy wektor $\color{brown}{\bar{P}}$ od współrzędnych tekstury, aby uzyskać ostateczne przesunięte współrzędne tekstury.
Warto zauważyć tutaj dzielenie viewDir.xy przez viewDir.z. Ponieważ wektor viewDir jest znormalizowany, viewDir.z będzie znajdował się gdzieś w zakresie od 0.0 do 1.0. Gdy viewDir jest w dużej mierze równoległy do powierzchni, jego składnik z jest bliski 0.0, a dzielenie zwraca znacznie większy wektor $\color{brown}{\bar{P}}$ w porównaniu do tego kiedy wektor viewDir jest w dużej mierze prostopadły do powierzchni. Zasadniczo zwiększamy rozmiar $\color{brown}{\bar{P}}$ w taki sposób, że przesuwa on współrzędne tekstury z większą skalą, patrząc na powierzchnię pod kątem w stosunku do widoku z góry; to daje bardziej realistyczne wyniki pod różnymi kątami.
Niektórzy ludzie wolą usunąć dzielenie przez viewDir.z z równania, ponieważ mapowanie paralaksy może powodować niepożądane wyniki pod różnymi kątami; technika jest wtedy nazywana jako
Uzyskane współrzędne tekstury są następnie używane do próbkowania innych tekstur (diffuse i normal), co daje bardzo ładny efekt przesunięcia, jak widać poniżej ze zmienną height_scale ustawioną na 0.1:
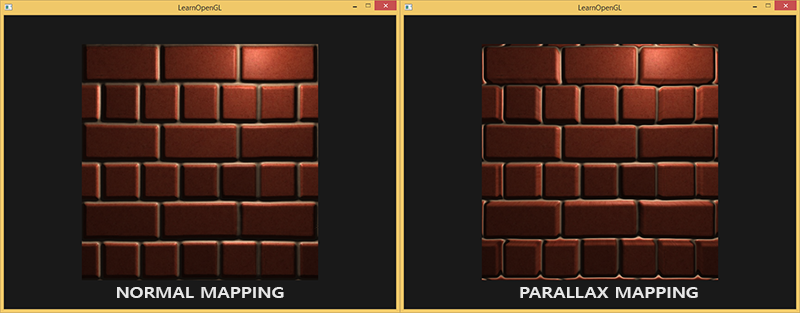
Tutaj możesz zobaczyć różnicę między normal mappingiem a mapowaniem paralaksy w połączeniu z normal mappingiem. Ponieważ mapowanie paralaksy próbuje symulować głębię, możliwe jest, że cegły nakładają się na inne w zależności od kierunku, z którego je oglądasz.
Nadal można zobaczyć kilka dziwnych artefaktów na granicy płaszczyzny z efektem mapowania paralaksy. Dzieje się tak, ponieważ na krawędziach płaszczyzny przesunięte współrzędne tekstury mogą przekraczać zakres [0, 1], co daje nierealistyczne wyniki w oparciu o tryb zawijania tekstury. Fajną sztuczką do rozwiązania tego problemu jest odrzucenie fragmentów za każdym razem, gdy pobierane są próbki poza domyślnym zakresem współrzędnych tekstury:
texCoords = ParallaxMapping(fs_in.TexCoords, viewDir);
if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0)
discard;
Wszystkie fragmenty z (przesuniętymi) współrzędnymi tekstur poza domyślnym zakresem zostają odrzucone, a mapowanie paralaksy daje odpowiedni wynik wokół krawędzi powierzchni. Zauważ, że ta sztuczka nie działa poprawnie na wszystkich typach powierzchni, ale po nałożeniu na płaszczyznę daje świetne wyniki, dzięki czemu wygląda tak, jakby płaszczyzna została faktycznie przemieszczona:
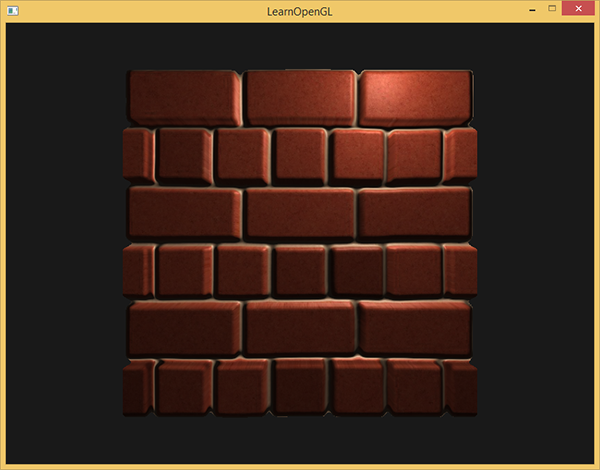
Możesz znaleźć kod źródłowy tutaj.
Wygląda to świetnie i jest dość szybkie - potrzebujemy tylko jednej dodatkowej próbki tekstury do mapowania paralaksy. Występuje jednak kilka problemów, ponieważ kiedy patrzy się na płaszczyznę pod kątem (podobnie jak w przypadku normal mappingu) algorytm daje nieprawidłowe wyniki dla dużych różnic wysokości, jak widać poniżej:
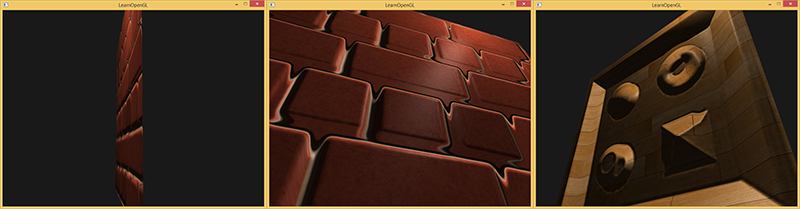
Powodem, że czasami nie działa to poprawnie, jest to, że jest to tylko przybliżenie mapowania przemieszczeń. Istnieje jednak kilka dodatkowych trików, które pozwalają nam uzyskać niemal perfekcyjne wyniki z dużymi zmianami wysokości, nawet jeśli patrzymy pod kątem. Na przykład, co jeśli zamiast jednej próbki pobierzemy wiele próbek, aby znaleźć najbliższy punkt do punktu $\color{blue}B$?
Steep Parallax Mapping
Steep Parallax Mapping jest rozszerzeniem nad mapowaniem paralaksy, ponieważ używa tych samych zasad, ale zamiast 1 próbki wymaga wielu próbek, aby lepiej przykuć wektor $\color{brown}{\bar{P}}$ do punktu $\color{blue}B$. Daje to o wiele lepsze wyniki, nawet przy wysokich zmianach wysokości, ponieważ dokładność tej techniki poprawia się dzięki większej liczbie próbek.
Ogólna koncepcja Steep Parallax Mapping polega na tym, że dzieli całkowity zakres głębokości na wiele warstw o tej samej wysokości/głębokości. Dla każdej z tych warstw próbkujemy mapę głębi przesuwając współrzędne tekstury wzdłuż kierunku $\color{brown}{\bar{P}}$, aż znajdziemy próbkowaną wartość głębokości, która jest poniżej wartości głębokości bieżącej warstwy. Spójrz na następujący obraz:
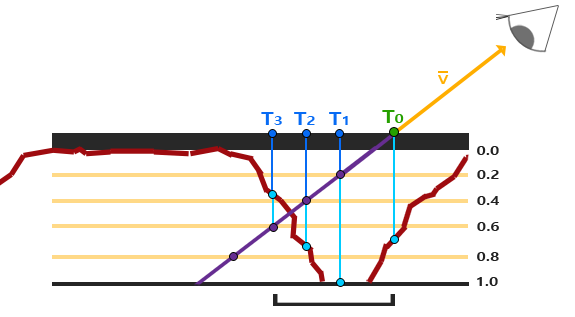
Przemierzamy warstwy głębokości od góry do dołu i dla każdej warstwy porównujemy jej wartość głębokości z wartością głębokości zapisaną w mapie głębi. Jeśli wartość głębi warstwy jest mniejsza niż wartość głębi mapy, oznacza to, że ta część wektora $\color{brown}{\bar{P}}$ nie znajduje się poniżej powierzchni. Kontynuujemy ten proces, dopóki głębokość warstwy nie przekroczy wartości zapisanej w mapie głębi: ten punkt znajduje się poniżej (przesuniętej) geometrii powierzchni.
W tym przykładzie widać, że wartość mapy głębi na drugiej warstwie (D(2) = 0.73) jest nadal niższa niż wartość głębi drugiej warstwy 0.4, więc kontynuujemy. W następnej iteracji wartość głębi warstwy 0.6 staje się wyższa niż wartość głębi próbki w mapie głębi (D(3) = 0.37). Możemy zatem przyjąć, że wektor $\color{brown}{\bar{P}}$ na trzeciej warstwie jest najbardziej realną pozycją przesuniętej geometrii. Możemy wtedy przyjąć przesunięcie współrzędnych tekstury $T_3$ z wektora $\color{brown}{\bar{P_3}}$, aby przesunąć współrzędne tekstury fragmentu. Możesz zobaczyć, jak zwiększa się dokładność przy większej liczbie warstw głębi.
Aby wdrożyć tę technikę, musimy tylko zmienić funkcję
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{
// number of depth layers
const float numLayers = 10;
// calculate the size of each layer
float layerDepth = 1.0 / numLayers;
// depth of current layer
float currentLayerDepth = 0.0;
// the amount to shift the texture coordinates per layer (from vector P)
vec2 P = viewDir.xy * height_scale;
vec2 deltaTexCoords = P / numLayers;
[...]
}
Tutaj najpierw określamy liczbę warstw, obliczamy głębokość każdej warstwy i na koniec obliczamy przesunięcie współrzędnych tekstury wzdłuż kierunku $\color{brown}{\bar{P}}$ na każdą warstwę .
Następnie iterujemy po wszystkich warstwach, zaczynając od góry, aż znajdziemy wartość mapy głębokości mniejszą niż wartość głębi warstwy:
// get initial values
vec2 currentTexCoords = texCoords;
float currentDepthMapValue = texture(depthMap, currentTexCoords).r;
while(currentLayerDepth < currentDepthMapValue)
{
// shift texture coordinates along direction of P
currentTexCoords -= deltaTexCoords;
// get depthmap value at current texture coordinates
currentDepthMapValue = texture(depthMap, currentTexCoords).r;
// get depth of next layer
currentLayerDepth += layerDepth;
}
return currentTexCoords;
Tutaj iterujemy po każdej warstwie głębi i zatrzymujemy się, kiedy znajdziemy przesunięcie współrzędnych tekstury wzdłuż wektora $\color{brown}{\bar{P}}$, które najpierw zwraca głębokość poniżej powierzchni (przesuniętej). Wynikowe przesunięcie jest odejmowane od współrzędnych tekstury fragmentu w celu uzyskania końcowego przesuniętego wektora współrzędnych tekstury, tym razem z dużo większą dokładnością w porównaniu do tradycyjnego mapowania paralaksy.
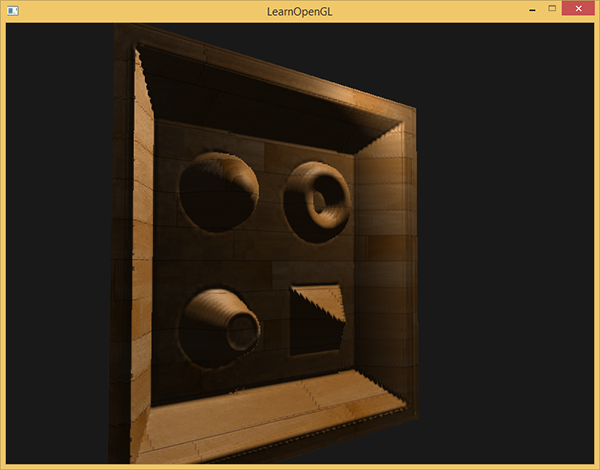
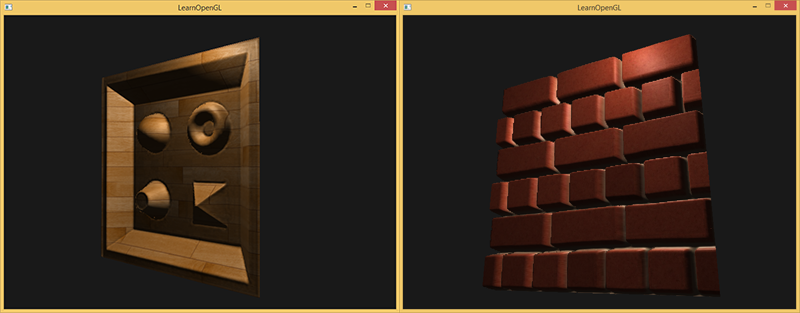
Przy około 10 próbkach, powierzchnia cegieł wygląda już bardziej wiarygodnie, nawet gdy patrzy się na nią pod kątem, ale Steep Parallax Mapping naprawdę wygląda dobrze, gdy ma złożoną powierzchnię z dużymi zmianami wysokości, jak wcześniej wyświetlana drewniana powierzchnia:
Możemy nieco ulepszyć algorytm, wykorzystując jedną z właściwości Parallax Mappingu. Patrząc prosto na powierzchnię, nie ma zbyt dużego przemieszczania tekstury, podczas gdy występuje duże przesunięcie podczas patrzenia na powierzchnię pod kątem (w obu przypadkach zwizualizuj kierunek patrzenia). Używając mniejszej ilości próbek, gdy patrzymy prosto na powierzchnię i większej ilości próbek, gdy patrzymy pod kątem, próbkujemy tylko potrzebną ilość razy:
const float minLayers = 8.0;
const float maxLayers = 32.0;
float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir)));
Tutaj bierzemy iloczyn skalarny viewDir i pozytywnego kierunku z i wykorzystujemy jego wynik do wyrównania liczby próbek bardziej do minLayers lub maxLayers bazując na kącie, pod którym patrzymy w kierunku powierzchni (zauważmy, że dodatni kierunek z jest równy wektorowi normalnemu powierzchni w przestrzeni stycznych). Gdybyśmy spojrzeli w kierunku równoległym do powierzchni, użylibyśmy w sumie 32 warstw.
Możesz znaleźć zaktualizowany kod źródłowy tutaj. Możesz również znaleźć powierzchnię drewnianego pudełka z zabawkami tutaj: diffuse, normal i depth.
Steep Parallax Mapping ma również swoje wady. Ponieważ technika oparta jest na skończonej liczbie próbek, uzyskujemy efekt aliasingu, a wyraźne rozróżnienia między warstwami można łatwo zauważyć:
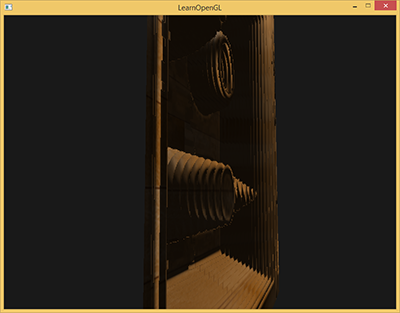
Możemy zmniejszyć ten problem, pobierając większą liczbę próbek, ale to szybko staje się zbyt dużym kosztem obliczeniowym. Istnieje kilka podejść, które mają na celu naprawienie tego problemu, poprzez nie pobieranie pierwszej pozycji poniżej powierzchni (przesuniętej), ale przez interpolację pomiędzy dwiema najbliższymi warstwami położenia, aby znaleźć dużo bliższe dopasowanie do $\color{blue}B$.
Dwa z bardziej popularnych podejść są nazywane
Parallax Occlusion Mapping
Parallax Occlusion Mapping oparty jest na tych samych zasadach co Steep Parallax Mapping, ale zamiast pobierać współrzędne tekstury z pierwszej warstwy głębi po kolizji, będziemy interpolować liniowo między warstwą głębi po i przed kolizją. Podstawę wagi interpolacji liniowej opieramy na tym, jak daleko jest wartość wysokości powierzchni od wartości warstwy głębi. Spójrz na poniższe zdjęcie, aby zrozumieć, jak to działa:
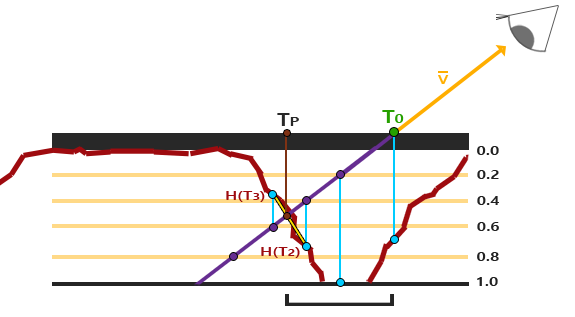
Jak widać, jest to w dużym stopniu podobne do Steep Parallax Mapping z dodatkowym krokiem interpolacji liniowej pomiędzy dwiema współrzędnymi tekstury warstw głębokości otaczających punkt przecięcia. Jest to ponownie przybliżenie, ale znacznie dokładniejsze niż Steep Parallax Mapping.
Kod Parallax Occlusion Mapping jest rozszerzeniem Steep Parallax Mapping i nie jest zbyt trudny:
[...] // steep parallax mapping code here
// get texture coordinates before collision (reverse operations)
vec2 prevTexCoords = currentTexCoords + deltaTexCoords;
// get depth after and before collision for linear interpolation
float afterDepth = currentDepthMapValue - currentLayerDepth;
float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth;
// interpolation of texture coordinates
float weight = afterDepth / (afterDepth - beforeDepth);
vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight);
return finalTexCoords;
Po znalezieniu warstwy głębokości po przecięciu (przesuniętej) geometrii powierzchni pobieramy również współrzędne tekstury warstwy głębi przed przecięciem. Następnie obliczamy odległość głębokości (przesuniętej) geometrii z odpowiednich warstw głębokości i interpolujemy te dwie wartości. Interpolacja liniowa jest podstawową interpolacją między współrzędnymi tekstury obu warstw. Funkcja zwraca ostatecznie końcowe interpolowane współrzędne tekstury.
Parallax Occlusion Mapping daje zaskakująco dobre wyniki i chociaż są widoczne pewne drobne artefakty i nadal są problemy z aliasingiem, to jest to generalnie dobry kompromis i widoczne tylko przy dużym zbliżeniu lub przy bardzo stromych kątach.
Możesz znaleźć kod źródłowy tutaj.
Parallax Mapping to świetna technika, która zwiększa szczegółowość Twojej sceny, ale zawiera kilka artefaktów, które musisz wziąć pod uwagę podczas jej używania. Najczęściej mapowanie paralaksy jest stosowane na powierzchniach podłogowych lub ściennych, gdzie nie jest łatwo określić konturu powierzchni, a kąt widzenia najczęściej jest z grubsza prostopadły do powierzchni. W ten sposób artefakty Parallax Mappingu nie są tak zauważalne i czynią z nich niesamowicie interesującą technikę zwiększania szczegółowości obiektów.
Dodatkowe materiały
- Parallax Occlusion Mapping in GLSL: świetny samouczek mapowania paralaksy autorstwa sunandblackcat.com.
- How Parallax Displacement Mapping Works: dobry film instruktażowy o tym, jak działa mapowanie paralaksy autorstwa TheBennyBox.