This is the Polish translation of In-Practice/2D-Game/Collisions/Collision-detection article of learnopengl.com tutorial series.

Podczas próby określenia, czy kolizja występuje między dwoma obiektami, zazwyczaj nie używamy danych samych obiektów, ponieważ obiekty te są często dość skomplikowane; to z kolei powoduje skomplikowane wykrywanie kolizji. Z tego powodu powszechną praktyką jest stosowanie prostszych kształtów (które zazwyczaj mają przyjemną matematyczną definicję) do wykrywania kolizji, które nakładamy na wierzch pierwotnego obiektu. Następnie sprawdzamy kolizje na podstawie tych prostych kształtów, co upraszcza kod i oszczędza dużo wydajności. Kilka przykładów takich kształtów kolizji (ang. collision shapes) to koła, sfery, prostokąty i sześciany; są one o wiele prostsze w porównaniu z siatkami z setkami trójkątów.

Chociaż dają one nam łatwiejsze i bardziej wydajne algorytmy wykrywania kolizji, prostsze kształty kolizji mają wspólną wadę polegającą na tym, że kształty te zwykle nie otaczają w pełni obiektu. Efekt jest taki, że można wykryć kolizję, która tak naprawdę nie kolidowała z rzeczywistym obiektem; należy zawsze pamiętać, że kształty te są jedynie przybliżeniami rzeczywistych kształtów.

Kolizje AABB - AABB

AABB oznacza axis-aligned bounding box (wyrównany do osi prostokąt otaczający), który jest prostokątnym kształtem kolizji wyrównanym do osi bazowej sceny, która w 2D jest wyrównana do osi X i Y. Ustawienie w osi oznacza, że ​​prostokątna ramka nie jest obracana, a jej krawędzie są równoległe do osi podstawy sceny (na przykład lewa i prawa krawędź są równoległe do osi y). Fakt, że te prostokąty są zawsze wyrównane do osi sceny, ułatwia obliczenia. Tutaj otaczamy obiekt piłki za pomocą AABB:

Niemal wszystkie obiekty w Breakout są obiektami opartymi na prostokątach, więc rozsądnie jest używać axis aligned bounding boxes do wykrywania kolizji. Dokładnie to zamierzamy zrobić.

Axis aligned bounding boxes można zdefiniować na kilka sposobów. Jednym ze sposobów definiowania AABB jest posiadanie pozycji z lewego górnego rogu i prawego dolnego rogu. Zdefiniowana przez nas klasa GameObject zawiera górną lewą pozycję (jej wektor Position) i możemy łatwo obliczyć jego dolną prawą pozycję, dodając jej rozmiar do górnej lewej pozycji (Position + Size). Wtedy, każdy GameObject zawierać będzie AABB, którego możemy użyć do obliczania kolizji.

Jak więc określić kolizje? Kolizja występuje, gdy dwa kształty zderzenia wchodzą w swoje rejony, np. kształt, który określa pierwszy obiekt, jest w pewien sposób wewnątrz kształtu drugiego obiektu. W przypadku AABB jest to dość łatwe do ustalenia ze względu na fakt, że są one wyrównane do osi sceny: sprawdzamy dla każdej osi, czy krawędzie dwóch obiektów na tej osi zachodzą na siebie. Zasadniczo sprawdzamy, czy krawędzie poziome zachodzą na siebie i czy krawędzie pionowe nakładają się na oba obiekty. Jeśli obie poziome krawędzie poziome i pionowe zachodzą na siebie, mamy kolizję.

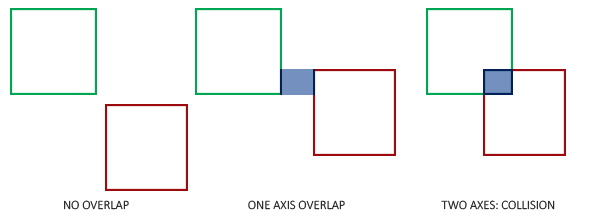
Tłumaczenie tego pojęcia na kod jest dość proste. Sprawdzamy czy obie osie nakładają się na siebie, jeśli tak, zwróć kolizję kolizję:

    GLboolean CheckCollision(GameObject &one, GameObject &two) // AABB - AABB collision
    {
        // Collision x-axis?
        bool collisionX = one.Position.x + one.Size.x >= two.Position.x &&
            two.Position.x + two.Size.x >= one.Position.x;
        // Collision y-axis?
        bool collisionY = one.Position.y + one.Size.y >= two.Position.y &&
            two.Position.y + two.Size.y >= one.Position.y;
        // Collision only if on both axes
        return collisionX && collisionY;
    }  

Sprawdzamy, czy prawa strona pierwszego obiektu jest większa niż lewa strona drugiego obiektu i jeśli prawa strona drugiego obiektu jest większa niż lewa strona pierwszego obiektu; podobnie dla osi pionowej. Jeśli masz problemy z wizualizacją tego, spróbuj narysować krawędzie/prostokąty na papierze i spróbuj ustalić to samemu.

Aby kod kolizji był trochę bardziej zorganizowany, dodajemy dodatkową funkcję do klasy Game:

    class Game
    {
        public:
            [...]
            void DoCollisions();
    };

W ramach DoCollisions sprawdzamy kolizje między obiektem piłki, a każdą cegłą w poziomie. Jeśli wykryjemy kolizję, ustawiamy właściwość Destroyed cegiełki na true, co również natychmiast zatrzymuje renderowanie tej cegły.

    void Game::DoCollisions()
    {
        for (GameObject &box : this->Levels[this->Level].Bricks)
        {
            if (!box.Destroyed)
            {
                if (CheckCollision(*Ball, box))
                {
                    if (!box.IsSolid)
                        box.Destroyed = GL_TRUE;
                }
            }
        }
    }  

Następnie musimy zaktualizować funkcję Update gry:

    void Game::Update(GLfloat dt)
    {
        // Update objects
        Ball->Move(dt, this->Width);
        // Check for collisions
        this->DoCollisions();
    }  

Jeśli teraz uruchomimy kod, piłka powinna wykryć kolizje z każdą z cegieł, i jeśli cegła nie jest niezniszczalna, cegła zostaje zniszczona. Jeśli uruchomisz grę, będzie wyglądać to mniej więcej tak:

Chociaż wykrywanie kolizji działa, nie jest ono zbyt precyzyjne, ponieważ piłka zderza się z większością cegieł, nie dotykając ich bezpośrednio. Zastosujmy zatem inną technikę wykrywania kolizji.

AABB - Wykrywanie kolizji koła

Ponieważ piłka jest obiektem w kształcie koła, AABB prawdopodobnie nie jest najlepszym wyborem kształtu kolizji piłki. Kod zderzenia uważa, że ​​piłka jest prostokątnym pudełkiem, więc piłka często zderza się z cegłą, mimo że sama kulka nie styka się jeszcze z cegłą.

Bardziej sensowne jest reprezentowanie piłki z kolistym kształtem zamiast AABB. Z tego powodu zawarliśmy zmienną Radius w obiekcie piłki. Aby zdefiniować kształt kolizji koła, potrzebujemy jedynie wektora pozycji i promień koła.

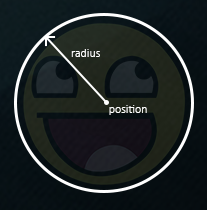
To oznacza, że ​​musimy zaktualizować algorytm wykrywania kolizji, ponieważ obecnie działa on tylko między dwoma AABB. Wykrywanie kolizji między okręgiem a prostokątem jest nieco bardziej skomplikowane, ale sztuczka wygląda następująco: znajdujemy punkt na AABB, który jest najbliżej koła, a jeśli odległość od koła do tego punktu jest mniejsza niż promień koła, mamy kolizję.

Najtrudniejszą częścią jest uzyskanie tego najbliższego punktu $\color{red}{\bar{P}}$ na AABB. Poniższy rysunek pokazuje, w jaki sposób możemy obliczyć ten punkt dla dowolnego AABB i koła:

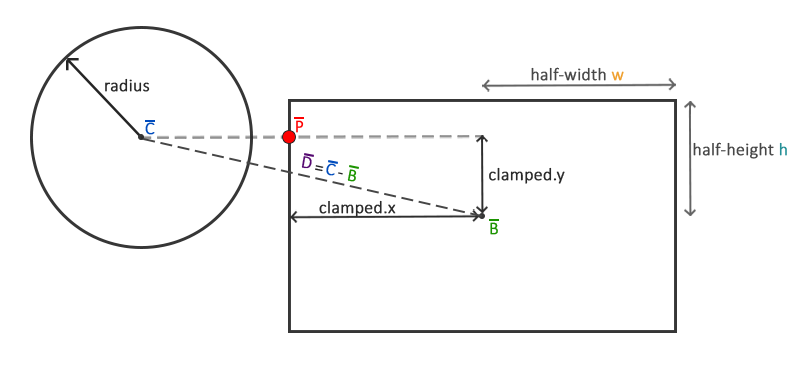
Najpierw musimy uzyskać wektor różnicy między centrum piłki $\color{blue}{\bar{C}}$ a centrum AABB $\color{green}{\bar{B}}$, aby uzyskać $\color{purple}{\bar{D}}$. Następnie musimy obciąć ten wektor $\color{purple}{\bar{D}}$ do połowy rozmiaru AABB $\color{orange}{w}$ i $\color{teal}{\bar{h}}$. Połowa rozmiaru prostokąta to odległości między środkiem prostokąta a jego krawędziami; zasadniczo jego rozmiar podzielony przez dwa. Zwraca to wektor pozycji, który zawsze znajduje się gdzieś na krawędzi AABB (chyba że środek koła znajduje się wewnątrz AABB).

Operacja clamp obcina wartość do wartości w podanym zakresie. Jest to często wyrażane jako:

    float clamp(float value, float min, float max) {
        return std::max(min, std::min(max, value));
    }  

Na przykład wartość 42.0f jest obcięta do 6.0f dla zakresu 3.0f i 6.0f, a wartość 4.20f zostanie obcięta do 4.20f. Obcinanie wektora 2D oznacza, że obcina się zarówno jego współrzędną x, jak i y do podanego zakresu.

Ten obcięty wektor $\color{red}{\bar{P}}$ jest wtedy najbliższym punktem od AABB do koła. Następnie musimy obliczyć nowy wektor różnicy $\color{purple}{\bar{D’}}$, który jest różnicą między środkiem koła $\color{blue}{\bar{C}}$ a wektorem $\color{red}{\bar{P}}$.

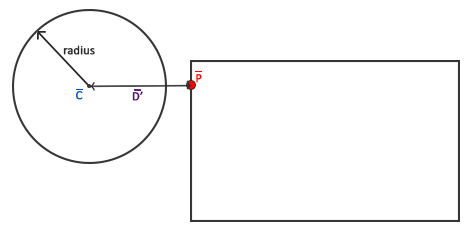
Teraz, gdy mamy wektor $\color{purple}{\bar{D’}}$ możemy porównać jego długość z promieniem koła, aby ustalić, czy mamy kolizję.

Wszystko to jest wyrażone w kodzie w następujący sposób:

    GLboolean CheckCollision(BallObject &one, GameObject &two) // AABB - Circle collision
    {
        // Get center point circle first 
        glm::vec2 center(one.Position + one.Radius);
        // Calculate AABB info (center, half-extents)
        glm::vec2 aabb_half_extents(two.Size.x / 2, two.Size.y / 2);
        glm::vec2 aabb_center(
            two.Position.x + aabb_half_extents.x, 
            two.Position.y + aabb_half_extents.y
        );
        // Get difference vector between both centers
        glm::vec2 difference = center - aabb_center;
        glm::vec2 clamped = glm::clamp(difference, -aabb_half_extents, aabb_half_extents);
        // Add clamped value to AABB_center and we get the value of box closest to circle
        glm::vec2 closest = aabb_center + clamped;
        // Retrieve vector between center circle and closest point AABB and check if length <= radius
        difference = closest - center;
        return glm::length(difference) < one.Radius;
    }      

Przeładowana funkcja CheckCollision została stworzona specjalnie dla BallObject i GameObject. Ponieważ nie zapisaliśmy informacji o kształcie kolizji w samych obiektach, musimy je obliczyć: najpierw obliczany jest środek piłki, następnie połowa rozmiaru AABB i jego środek.

Korzystając z tych kształtów kolizji, obliczamy wektor $\color{purple}{\bar{D}}$ jako różnicę, którą następnie obcinamy do danego zakresu i dodajemy do środka AABB, aby uzyskać najbliższy punkt $\color{red}{\bar{P}}$. Następnie obliczamy wektor różnicy $\color{purple}{\bar{D’}}$ pomiędzy center i closest i określamy, czy oba kształty się zderzyły, czy nie.

Ponieważ poprzednio wywołaliśmy CheckCollision z piłką jako pierwszym argumentem, nie musimy zmieniać żadnego kodu, ponieważ mamy przeładowany wariant funkcji CheckCollision, który sam to wykryje. Rezultatem jest teraz znacznie bardziej precyzyjny algorytm wykrywania kolizji.

Wydaje się, że wszystko działa, ale nadal coś jest nie tak. Właściwie wykonujemy wykrywanie kolizji, ale piłka nie reaguje w żaden sposób na kolizje. Musimy reagować na kolizje, np. aktualizować położenie piłki i/lub prędkość w momencie kolizji. To jest temat następnego samouczka.