This is the Polish translation of In-Practice/2D-Game/Collisions/Collision-resolution article of learnopengl.com tutorial series.
Pod koniec ostatniego tutoriala mieliśmy działający kod wykrywania kolizji. Kula nie reaguje jednak w żaden sposób na wykryte kolizje; po prostu przesuwa się prosto kolidując ze wszystkimi napotkanymi cegłami. Chcemy, aby piłka odbijała się od każdej uderzonej cegły. W tym samouczku omówimy, w jaki sposób możemy osiągnąć tak zwane
Ilekroć dojdzie do kolizji, chcemy, aby wydarzyły się dwie rzeczy: chcemy zmienić położenie piłki, aby nie znajdowała się ona już wewnątrz drugiego obiektu, a po drugie, chcemy zmienić kierunek prędkości kuli, aby odbijała się od napotkanego obiektu.
Repozycjonowanie kolizji
Aby ustawić obiekt kuli poza zderzanym AABB, musimy określić odległość, jaką piłka przebiła przez kształt otaczający. W tym celu powrócimy do schematów z poprzedniego samouczka:
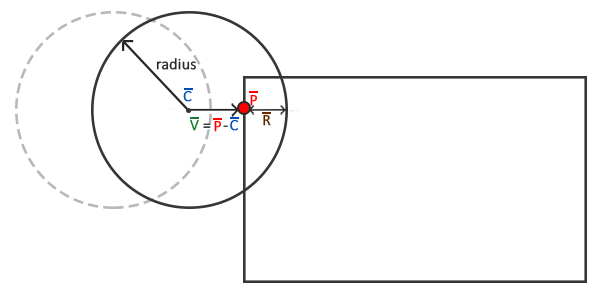
Tutaj piłka przesunęła się nieznacznie do środka AABB i wykryto kolizję. Teraz chcemy usunąć piłkę z kształtu AABB tak, aby dotykała tylko AABB, jakby nie doszło do kolizji. Aby dowiedzieć się, o ile musimy przesunąć piłkę z AABB, musimy pobrać wektor $\color{brown}{\bar{R}}$, który jest poziomem penetracji AABB. Aby uzyskać wektor $\color{brown}{\bar{R}}$ odejmujemy $\color{green}{\bar{V}}$ od promienia piłki. Wektor $\color{green}{\bar{V}}$ to różnica między najbliższym punktem $\color{red}{\bar{P}}$ a środkiem kuli $\color{blue}{\bar{C}}$.
Znając $ \color{brown}{\bar{R}}$, przesuwamy pozycję piłki o $\color{brown}{\bar{R}}$ i umieszczamy piłkę bezpośrednio obok AABB; piłka jest teraz prawidłowo ustawiona.
Kierunek kolizji
Następnie musimy dowiedzieć się, jak zaktualizować prędkość piłki po kolizji. W grze Breakout stosujemy następujące zasady, aby zmienić prędkość piłki:
- Jeżeli piłka zderza się z prawą lub lewą częścią AABB, jej prędkość pozioma (
x) jest odwracana. - Jeżeli piłka zderza się z dolną lub górną częścią AABB, jej prędkość pionowa (
y) jest odwracana.
Ale jak możemy wymyślić kierunek, w którym piłka uderzyła w AABB? Istnieje kilka podejść do tego problemu, a jednym z nich jest to, że zamiast 1 AABB używamy 4 AABB dla każdej cegły, którą pozycjonujemy na jednym z jej brzegów. W ten sposób możemy ustalić, który AABB, a zatem, która krawędź została trafiona. Istnieje jednak prostsze podejście przy pomocy iloczynu skalarnego.
Prawdopodobnie nadal pamiętasz z tutoriala transformacje, że iloczyn skalarny daje nam kąt pomiędzy dwoma znormalizowanymi wektorami. Co by było, gdybyśmy zdefiniowali cztery wektory wskazujące północ, południe, zachód lub wschód i obliczylibyśmy iloczyn skalarny między nimi a danym wektorem? Otrzymany wynik iloczynu skalarnego między tymi kierunkami i danym wektorem, który jest najwyższy (maksymalna wartość iloczynu skalarnego to 1.0f, który reprezentuje kąt 0 stopni), jest wówczas kierunkiem wektora.
Ta procedura wygląda następująco:
Direction VectorDirection(glm::vec2 target)
{
glm::vec2 compass[] = {
glm::vec2(0.0f, 1.0f), // up
glm::vec2(1.0f, 0.0f), // right
glm::vec2(0.0f, -1.0f), // down
glm::vec2(-1.0f, 0.0f) // left
};
GLfloat max = 0.0f;
GLuint best_match = -1;
for (GLuint i = 0; i < 4; i++)
{
GLfloat dot_product = glm::dot(glm::normalize(target), compass[i]);
if (dot_product > max)
{
max = dot_product;
best_match = i;
}
}
return (Direction)best_match;
}
Funkcja porównuje target z każdym z wektorów kierunkowych w tablicy compass. Tutaj Direction jest częścią typu enum zdefiniowanego w pliku nagłówkowym klasy Game:
enum Direction {
UP,
RIGHT,
DOWN,
LEFT
};
Teraz, gdy wiemy, jak uzyskać wektor $\color{brown}{\bar{R}}$ i jak określić kierunek, w którym piłka uderza w AABB, możemy zacząć pisać kod reakcji na kolizje.
AABB - reagowanie na kolizje koła
Aby obliczyć wymagane wartości reakcji kolizji, potrzebujemy nieco więcej informacji z funkcji kolizji niż tylko true lub false, więc zwrócimy tuple w nagłówku <tuple>.
Aby kod był trochę bardziej uporządkowany, stworzymy nowy typ dla danych kolizji o nazwie
typedef std::tuple<GLboolean, Direction, glm::vec2> Collision;
Następnie musimy zmienić kod funkcji true lub false, ale także wektor kierunku i różnicy:
Collision CheckCollision(BallObject &one, GameObject &two) // AABB - AABB collision
{
[...]
if (glm::length(difference) <= one.Radius)
return std::make_tuple(GL_TRUE, VectorDirection(difference), difference);
else
return std::make_tuple(GL_FALSE, UP, glm::vec2(0, 0));
}
Funkcja
void Game::DoCollisions()
{
for (GameObject &box : this->Levels[this->Level].Bricks)
{
if (!box.Destroyed)
{
Collision collision = CheckCollision(*Ball, box);
if (std::get<0>(collision)) // If collision is true
{
// Destroy block if not solid
if (!box.IsSolid)
box.Destroyed = GL_TRUE;
// Collision resolution
Direction dir = std::get<1>(collision);
glm::vec2 diff_vector = std::get<2>(collision);
if (dir == LEFT || dir == RIGHT) // Horizontal collision
{
Ball->Velocity.x = -Ball->Velocity.x; // Reverse horizontal velocity
// Relocate
GLfloat penetration = Ball->Radius - std::abs(diff_vector.x);
if (dir == LEFT)
Ball->Position.x += penetration; // Move ball to right
else
Ball->Position.x -= penetration; // Move ball to left;
}
else // Vertical collision
{
Ball->Velocity.y = -Ball->Velocity.y; // Reverse vertical velocity
// Relocate
GLfloat penetration = Ball->Radius - std::abs(diff_vector.y);
if (dir == UP)
Ball->Position.y -= penetration; // Move ball back up
else
Ball->Position.y += penetration; // Move ball back down
}
}
}
}
}
Nie przejmuj się zbytnio złożonością funkcji, ponieważ jest to w zasadzie bezpośrednie tłumaczenie dotychczas wprowadzonych koncepcji. Najpierw sprawdzamy kolizję, a jeśli wystąpiła, niszczymy blok. Następnie uzyskujemy kierunek kolizji dir i wektor $\color{green}{\bar{V}}$ jako diff_vector z tuple, a na końcu reagujemy na kolizję.
Najpierw sprawdzamy, czy kierunek kolizji jest poziomy czy pionowy, a następnie odpowiednio odwracamy prędkość. Jeśli jest poziomo, obliczamy wartość penetracji $\color{brown}R$ z komponentu x wektora diff_vector i albo dodajemy, albo odejmujemy od pozycji piłki w oparciu o jej kierunek. To samo dotyczy kolizji pionowych, ale tym razem operujemy na składniku y wszystkich wektorów.
Uruchomienie aplikacji powinno teraz dać ci działające kolizje, ale prawdopodobnie trudno jest dostrzec ich efekt, ponieważ piłka odbije się w kierunku dolnej krawędzi, gdy tylko uderzy w pojedynczy blok i zgubi się na zawsze. Możemy to naprawić, poprzez ustanowienie kolizji z wiosłem gracza.
Gracz - kolizje piłki
Zderzenia między piłką a graczem są nieco inne niż te, o których wcześniej rozmawialiśmy, ponieważ tym razem prędkość pozioma piłki powinna być aktualizowana na podstawie tego, jak daleko od środka wiosła uderzyła piłka. Im dalej piłka uderza od środka wiosła, tym silniejsza powinna być jego prędkość pozioma.
void Game::DoCollisions()
{
[...]
Collision result = CheckCollision(*Ball, *Player);
if (!Ball->Stuck && std::get<0>(result))
{
// Check where it hit the board, and change velocity based on where it hit the board
GLfloat centerBoard = Player->Position.x + Player->Size.x / 2;
GLfloat distance = (Ball->Position.x + Ball->Radius) - centerBoard;
GLfloat percentage = distance / (Player->Size.x / 2);
// Then move accordingly
GLfloat strength = 2.0f;
glm::vec2 oldVelocity = Ball->Velocity;
Ball->Velocity.x = INITIAL_BALL_VELOCITY.x * percentage * strength;
Ball->Velocity.y = -Ball->Velocity.y;
Ball->Velocity = glm::normalize(Ball->Velocity) * glm::length(oldVelocity);
}
}
Po sprawdzeniu kolizji pomiędzy piłką a każdą cegłą, sprawdzamy, czy piłka zderzyła się z wiosłem gracza. Jeśli tak (a piłka nie przykleja się do wiosła), obliczamy procent odległości środka piłki od środka wiosła w stosunku do połowy wiosła. Pozioma prędkość piłki jest następnie aktualizowana w oparciu o odległość od środka wiosła. Oprócz aktualizacji prędkości poziomej musimy również odwrócić prędkość y.
Zwróć uwagę, że stara prędkość jest zapisywana jako oldVelocity. Powodem przechowywania starej prędkości jest to, że aktualizujemy jedynie prędkość poziomą wektora prędkości kulki, utrzymując stałą prędkość y. Oznaczałoby to, że długość wektora stale się zmienia, co powoduje, że wektor prędkości piłki jest znacznie większy (i tym samym silniejszy), jeśli piłka uderzyła w krawędź wiosła w porównaniu z piłką, która uderzyłaby w środek wiosła. Z tego powodu nowy wektor prędkości jest znormalizowany i mnożony przez długość starego wektora prędkości. W ten sposób siła, a tym samym prędkość piłki jest zawsze stała, niezależnie od tego, gdzie uderzy w wiosło.
Lepkie wiosło
Mogłeś lub nie zauważyłeś, że po uruchomieniu kodu, nadal istnieje duży problem z reakcją kolizji gracza i piłki. Poniższy film wyraźnie pokazuje, co może się stać:
Ten problem nazywa się problemem
Możemy łatwo naprawić to zachowanie, wprowadzając mały hack, który jest możliwy dzięki temu, że możemy założyć, że zawsze mamy kolizję od góry wiosła. Zamiast odwracać prędkość y, po prostu zawsze zwracamy dodatni kierunek y, więc kiedy piłka utknie w środku wiosła, natychmiast się uwolni.
//Ball->Velocity.y = -Ball->Velocity.y;
Ball->Velocity.y = -1 * abs(Ball->Velocity.y);
Jeśli się wysilisz to, zobaczysz, że efekt jest nadal zauważalny, ale osobiście uważam, że jest to akceptowalny kompromis.
Dolna krawędź
Jedyną rzeczą, której wciąż brakuje w klasycznym przepisie na Breakout, jest pewien stan strat, który resetuje poziom i pozycję gracza. W ramach funkcji
void Game::Update(GLfloat dt)
{
[...]
if (Ball->Position.y >= this->Height) // Did ball reach bottom edge?
{
this->ResetLevel();
this->ResetPlayer();
}
}
Funkcje
Właśnie skończyliśmy tworzyć klona klasycznej gry Breakout z podobną mechaniką. Tutaj znajdziesz kod źródłowy klasy gry: nagłówek, kod.
Kilka notatek
Wykrywanie kolizji jest trudnym tematem tworzenia gier wideo i prawdopodobnie jego największym wyzwaniem. Większość schematów wykrywania i reakcji kolizji jest połączona z silnikami fizyki, jak w większości współczesnych gier. Schemat kolizji użyty do gry Breakout to bardzo prosty schemat dla tego typu gry.
Należy podkreślić, że ten rodzaj wykrywania kolizji i reakcji kolizji nie jest doskonały. Oblicza możliwe kolizje tylko na raz na klatkę i tylko dla dokładnie takich pozycji, jakie są w tym czasie; oznacza to, że jeśli obiekt miałby taką prędkość, że przechodziłby przez inny obiekt w obrębie pojedynczej ramki, wyglądałoby tak, jakby nigdy nie kolidował z tym obiektem. Jeśli więc spadają klatki lub osiągasz wystarczająco wysokie prędkości, ten schemat wykrywania kolizji nie będzie się działał dobrze.
Kilka problemów, które wciąż mogą wystąpić:
- Jeśli piłka porusza się zbyt szybko, może przeskakiwać nad obiektem w obrębie jednej klatki, nie wykrywając żadnych kolizji.
- Jeśli piłka trafi więcej niż jeden obiekt w obrębie pojedynczej ramki, wykryje dwie kolizje i dwa razy odwróci swoją prędkość; nie wpływając na pierwotną prędkość.
- Uderzenie w róg cegiełki może odwrócić prędkość piłki w niewłaściwym kierunku, ponieważ odległość, jaką pokonuje w pojedynczej ramce, może sprawić, że różnica między
VectorDirection powróci w pionie lub poziomie.
Te tutoriale mają jednak na celu nauczyć czytelników podstaw kilku aspektów grafiki i tworzenia gier. Z tego powodu ten schemat kolizji spełnia swój cel; jest zrozumiały i działa całkiem dobrze w normalnych scenariuszach. Należy pamiętać, że istnieją lepsze (bardziej skomplikowane) schematy kolizji, które działają całkiem dobrze w prawie wszystkich scenariuszach (w tym obiektach ruchomych), takie jak
Na szczęście istnieją duże, praktyczne i często dość wydajne silniki fizyki (z kolizjami niezależnymi od czasu) do użytku we własnych grach. Jeśli chcesz zagłębić się w takie systemy lub potrzebujesz bardziej zaawansowanej fizyki i masz problemy z matematyką, to Box2D jest idealną biblioteką fizyki 2D do implementacji fizyki i wykrywania kolizji w twojej aplikacji.